线性回归

优质

小牛编辑

123浏览

2023-12-01

1、代价函数

$$J(\theta ) = \frac{1}{{2{\text{m}}}}\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^2}} $$
其中： $${h_\theta }(x) = {\theta _0} + {\theta _1}{x_1} + {\theta _2}{x_2} + ...$$
下面就是要求出theta，使代价最小，即代表我们拟合出来的方程距离真实值最近
共有m条数据，其中 $${{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^2}}$$ 代表我们要拟合出来的方程到真实值距离的平方，平方的原因是因为可能有负值，正负可能会抵消
前面有系数 2 的原因是下面求梯度是对每个变量求偏导，2 可以消去

实现代码：

# 计算代价函数
def computerCost(X,y,theta):
  m = len(y)
  J = 0
  
  J = (np.transpose(X*theta-y))*(X*theta-y)/(2*m) #计算代价J
  return J

注意这里的X是真实数据前加了一列1，因为有theta(0)

2、梯度下降算法

代价函数对 $${{\theta _j}}$$ 求偏导得到：$$\frac{{\partial J(\theta )}}{{\partial {\theta j}}} = \frac{1}{m}\sum\limits{i = 1}^m {[({h_\theta }({x^{(i)}}) - {y^{(i)}})x_j^{(i)}]} $$
所以对theta的更新可以写为：$${\theta j} = {\theta j} - \alpha \frac{1}{m}\sum\limits{i = 1}^m {[({h\theta }({x^{(i)}}) - {y^{(i)}})x_j^{(i)}]} $$
其中 $$\alpha $$ 为学习速率，控制梯度下降的速度，一般取 0.01,0.03,0.1,0.3.....
为什么梯度下降可以逐步减小代价函数
假设函数f(x)
泰勒展开：f(x+△x)=f(x)+f'(x)*△x+o(△x)
令：△x=-α*f'(x)，即负梯度方向乘以一个很小的步长α
将△x 代入泰勒展开式中：f(x+△x)=f(x)-α*[f'(x)]²+o(△x)
可以看出，α是取得很小的正数，[f'(x)]²也是正数，所以可以得出：f(x+△x)<=f(x)
所以沿着负梯度放下，函数在减小，多维情况一样。

实现代码

# 梯度下降算法
def gradientDescent(X,y,theta,alpha,num_iters):
  m = len(y)    
  n = len(theta)
  
  temp = np.matrix(np.zeros((n,num_iters)))   # 暂存每次迭代计算的theta，转化为矩阵形式
  
  
  J_history = np.zeros((num_iters,1)) #记录每次迭代计算的代价值
  
  for i in range(num_iters):  # 遍历迭代次数  
    h = np.dot(X,theta)   # 计算内积，matrix可以直接乘
    temp[:,i] = theta - ((alpha/m)*(np.dot(np.transpose(X),h-y)))   #梯度的计算
    theta = temp[:,i]
    J_history[i] = computerCost(X,y,theta)    #调用计算代价函数
    print '.',    
  return theta,J_history

3、均值归一化

目的是使数据都缩放到一个范围内，便于使用梯度下降算法 $${x_i} = \frac{{{x_i} - {\mu _i}}}{{{s_i}}}$$，其中 $${{\mu _i}}$$ 为所有此 feture 数据的平均值，$${{s_i}}$$ 可以是最大值-最小值，也可以是这个 feature 对应的数据的标准差。

实现代码：

# 归一化feature
def featureNormaliza(X):
  X_norm = np.array(X)      #将X转化为numpy数组对象，才可以进行矩阵的运算
  #定义所需变量
  mu = np.zeros((1,X.shape[1]))   
  sigma = np.zeros((1,X.shape[1]))
  
  mu = np.mean(X_norm,0)      # 求每一列的平均值（0指定为列，1代表行）
  sigma = np.std(X_norm,0)    # 求每一列的标准差
  for i in range(X.shape[1]):   # 遍历列
    X_norm[:,i] = (X_norm[:,i]-mu[i])/sigma[i]  # 归一化
  
  return X_norm,mu,sigma

注意预测的时候也需要均值归一化数据

4、最终运行结果

代价随迭代次数的变化

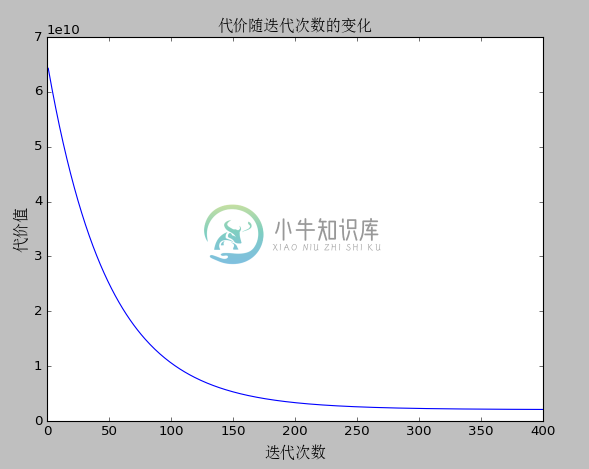
5、使用 scikit-learn 库中的线性模型实现

导入包

from sklearn import linear_model
from sklearn.preprocessing import StandardScaler  #引入缩放的包

归一化

  # 归一化操作
  scaler = StandardScaler()   
  scaler.fit(X)
  x_train = scaler.transform(X)
  x_test = scaler.transform(np.array([1650,3]))

线性模型拟合

  # 线性模型拟合
  model = linear_model.LinearRegression()
  model.fit(x_train, y)

预测

  #预测结果
  result = model.predict(x_test)