逻辑回归 手写数字识别 OneVsAll
优质
小牛编辑
113浏览
2023-12-01
1、随机显示 100 个数字
我没有使用 scikit-learn 中的数据集,像素是 20*20px,彩色图如下

灰度图:
实现代码:
# 显示100个数字
def display_data(imgData):
sum = 0
'''
显示100个数(若是一个一个绘制将会非常慢,可以将要画的数字整理好,放到一个矩阵中,显示这个矩阵即可)
- 初始化一个二维数组
- 将每行的数据调整成图像的矩阵,放进二维数组
- 显示即可
'''
pad = 1
display_array = -np.ones((pad+10*(20+pad),pad+10*(20+pad)))
for i in range(10):
for j in range(10):
display_array[pad+i*(20+pad):pad+i*(20+pad)+20,pad+j*(20+pad):pad+j*(20+pad)+20] = (imgData[sum,:].reshape(20,20,order="F")) # order=F指定以列优先,在matlab中是这样的,python中需要指定,默认以行
sum += 1
plt.imshow(display_array,cmap='gray') #显示灰度图像
plt.axis('off')
plt.show()
2、OneVsAll
如何利用逻辑回归解决多分类的问题,OneVsAll 就是把当前某一类看成一类,其他所有类别看作一类,这样有成了二分类的问题了
如下图,把途中的数据分成三类,先把红色的看成一类,把其他的看作另外一类,进行逻辑回归,然后把蓝色的看成一类,其他的再看成一类,以此类推...
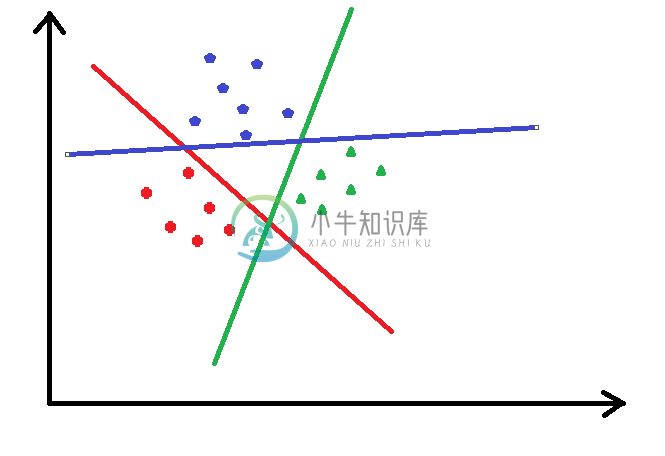
可以看出大于2类的情况下,有多少类就要进行多少次的逻辑回归分类
3、手写数字识别
共有0-9,10个数字,需要10次分类
由于数据集y给出的是 0,1,2...9 的数字,而进行逻辑回归需要 0/1 的 label 标记,所以需要对 y 处理
说一下数据集,前 500 个是 0,500-1000 是1,...,所以如下图,处理后的 y,前500行的第一列是1,其余都是0,500-1000行第二列是1,其余都是0....

然后调用梯度下降算法求解 theta
实现代码:
# 求每个分类的theta,最后返回所有的all_theta
def oneVsAll(X,y,num_labels,Lambda):
# 初始化变量
m,n = X.shape
all_theta = np.zeros((n+1,num_labels)) # 每一列对应相应分类的theta,共10列
X = np.hstack((np.ones((m,1)),X)) # X前补上一列1的偏置bias
class_y = np.zeros((m,num_labels)) # 数据的y对应0-9,需要映射为0/1的关系
initial_theta = np.zeros((n+1,1)) # 初始化一个分类的theta
# 映射y
for i in range(num_labels):
class_y[:,i] = np.int32(y==i).reshape(1,-1) # 注意reshape(1,-1)才可以赋值
#np.savetxt("class_y.csv", class_y[0:600,:], delimiter=',')
'''遍历每个分类,计算对应的theta值'''
for i in range(num_labels):
result = optimize.fmin_bfgs(costFunction, initial_theta, fprime=gradient, args=(X,class_y[:,i],Lambda)) # 调用梯度下降的优化方法
all_theta[:,i] = result.reshape(1,-1) # 放入all_theta中
all_theta = np.transpose(all_theta)
return all_theta
4、预测
之前说过,预测的结果是一个概率值,利用学习出来的 theta 代入预测的S型函数中,每行的最大值就是是某个数字的最大概率,所在的列号就是预测的数字的真实值,因为在分类时,所有为0的将y映射在第一列,为1的映射在第二列,依次类推
实现代码:
# 预测
def predict_oneVsAll(all_theta,X):
m = X.shape[0]
num_labels = all_theta.shape[0]
p = np.zeros((m,1))
X = np.hstack((np.ones((m,1)),X)) #在X最前面加一列1
h = sigmoid(np.dot(X,np.transpose(all_theta))) #预测
'''
返回h中每一行最大值所在的列号
- np.max(h, axis=1)返回h中每一行的最大值(是某个数字的最大概率)
- 最后where找到的最大概率所在的列号(列号即是对应的数字)
'''
p = np.array(np.where(h[0,:] == np.max(h, axis=1)[0]))
for i in np.arange(1, m):
t = np.array(np.where(h[i,:] == np.max(h, axis=1)[i]))
p = np.vstack((p,t))
return p
5、运行结果
10次分类,在训练集上的准确度:

6、使用 scikit-learn 库中的逻辑回归模型实现
1、导入包
from scipy import io as spio
import numpy as np
from sklearn import svm
from sklearn.linear_model import LogisticRegression
2、加载数据
data = loadmat_data("data_digits.mat")
X = data['X'] # 获取X数据,每一行对应一个数字20x20px
y = data['y'] # 这里读取mat文件y的shape=(5000, 1)
y = np.ravel(y) # 调用sklearn需要转化成一维的(5000,)
3、拟合模型
model = LogisticRegression()
model.fit(X, y) # 拟合
4、预测
predict = model.predict(X) #预测
print u"预测准确度为:%f%%"%np.mean(np.float64(predict == y)*100)
5、输出结果(在训练集上的准确度)


