PCA 主成分分析(降维)
优质
小牛编辑
120浏览
2023-12-01
1、用处
- 数据压缩(Data Compression),使程序运行更快
- 可视化数据,例如
3D-->2D等
2、2D-->1D,nD-->kD
如下图所示,所有数据点可以投影到一条直线,是投影距离的平方和(投影误差)最小
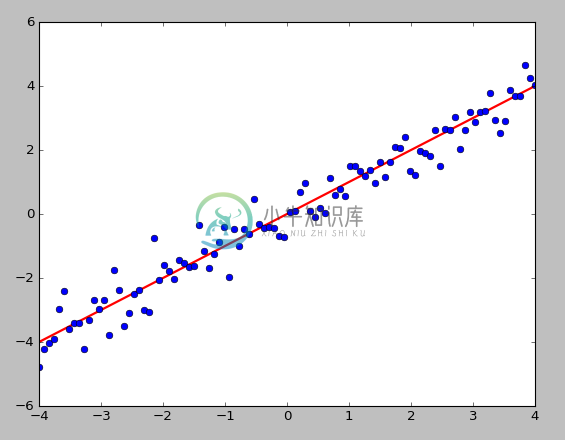
- 注意数据需要
归一化处理 - 思路是找
1个向量u,所有数据投影到上面使投影距离最小 - 那么
nD-->kD就是找k个向量 $$$${u^{(1)}},{u^{(2)}} \ldots {u^{(k)}}$$$$ ,所有数据投影到上面使投影误差最小 - eg:3D-->2D,2个向量 $$$${u^{(1)}},{u^{(2)}}$$$$ 就代表一个平面了,所有点投影到这个平面的投影误差最小即可
3、主成分分析PCA与线性回归的区别
- 线性回归是找
x与y的关系,然后用于预测y PCA是找一个投影面,最小化data到这个投影面的投影误差
4、PCA降维过程
- 数据预处理(均值归一化)
- 公式: $$$${\rm{x}}_j^{(i)} = {{{\rm{x}}_j^{(i)} - {u_j}} \over {{s_j}}}$$$$
- 就是减去对应feature的均值,然后除以对应特征的标准差(也可以是最大值-最小值)
实现代码:
# 归一化数据
def featureNormalize(X):
'''(每一个数据-当前列的均值)/当前列的标准差'''
n = X.shape[1]
mu = np.zeros((1,n));
sigma = np.zeros((1,n))
mu = np.mean(X,axis=0)
sigma = np.std(X,axis=0)
for i in range(n):
X[:,i] = (X[:,i]-mu[i])/sigma[i]
return X,mu,sigma
- 计算
协方差矩阵Σ(Covariance Matrix): $$$$\Sigma = {1 \over m}\sum\limits_{i = 1}^n {{x^{(i)}}{{({x^{(i)}})}^T}} $$$$ - 注意这里的
Σ和求和符号不同 - 协方差矩阵
对称正定(不理解正定的看看线代) - 大小为
nxn,n为feature的维度
实现代码:
Sigma = np.dot(np.transpose(X_norm),X_norm)/m # 求Sigma
- 计算
Σ的特征值和特征向量 - 可以是用
svd奇异值分解函数:U,S,V = svd(Σ) - 返回的是与
Σ同样大小的对角阵S(由Σ的特征值组成)[注意:matlab中函数返回的是对角阵,在python中返回的是一个向量,节省空间] - 还有两个酉矩阵U和V,且 $$$$\Sigma = US{V^T}$$$$
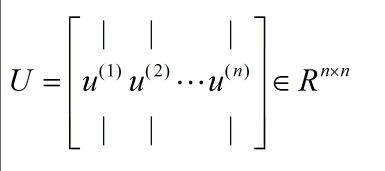
- 注意:
svd函数求出的S是按特征值降序排列的,若不是使用svd,需要按特征值大小重新排列U - 降维
- 选取
U中的前K列(假设要降为K维) 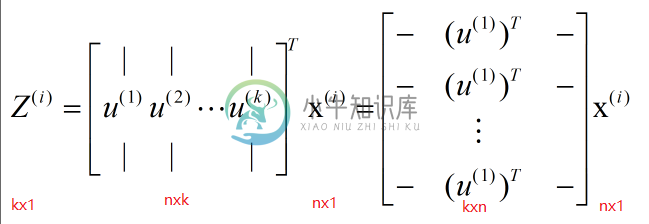
Z就是对应降维之后的数据
实现代码:
# 映射数据
def projectData(X_norm,U,K):
Z = np.zeros((X_norm.shape[0],K))
U_reduce = U[:,0:K] # 取前K个
Z = np.dot(X_norm,U_reduce)
return Z
- 过程总结:
Sigma = X'*X/mU,S,V = svd(Sigma)Ureduce = U[:,0:k]Z = Ureduce'*x
5、数据恢复
- 因为: $$$${Z^{(i)}} = U_{reduce}^T*{X^{(i)}}$$$$
- 所以: $$$${X_{approx}} = {(U_{reduce}^T)^{ - 1}}Z$$$$ (注意这里是X的近似值)
- 又因为
Ureduce为正定矩阵,【正定矩阵满足: $$$$A{A^T} = {A^T}A = E$$$$ ,所以: $$$${A^{ - 1}} = {A^T}$$$$ 】,所以这里: - $$$${X_{approx}} = {(U_{reduce}^{ - 1})^{ - 1}}Z = {U_{reduce}}Z$$$$
实现代码:
# 恢复数据
def recoverData(Z,U,K):
X_rec = np.zeros((Z.shape[0],U.shape[0]))
U_recude = U[:,0:K]
X_rec = np.dot(Z,np.transpose(U_recude)) # 还原数据(近似)
return X_rec
6、主成分个数的选择(即要降的维度)
如何选择
- 投影误差(project error): $$$${1 \over m}\sum\limits_{i = 1}^m {||{x^{(i)}} - x_{approx}^{(i)}|{|^2}} $$$$
- 总变差(total variation): $$$${1 \over m}\sum\limits_{i = 1}^m {||{x^{(i)}}|{|^2}} $$$$
- 若误差率(error ratio): $$$${{{1 \over m}\sum\limits_{i = 1}^m {||{x^{(i)}} - x_{approx}^{(i)}|{|^2}} } \over {{1 \over m}\sum\limits_{i = 1}^m {||{x^{(i)}}|{|^2}} }} \le 0.01$$$$ ,则称
99%保留差异性 - 误差率一般取
1%,5%,10%等
如何实现
- 若是一个个试的话代价太大
- 之前
U,S,V = svd(Sigma),我们得到了S,这里误差率error ratio:
$$$$error{\kern 1pt} ;ratio = 1 - {{\sum\limits_{i = 1}^k {{S_{ii}}} } \over {\sum\limits_{i = 1}^n {{S_{ii}}} }} \le threshold$$$$ - 可以一点点增加
K尝试。
7、使用建议
- 不要使用PCA去解决过拟合问题
Overfitting,还是使用正则化的方法(如果保留了很高的差异性还是可以的) - 只有在原数据上有好的结果,但是运行很慢,才考虑使用PCA
8、运行结果
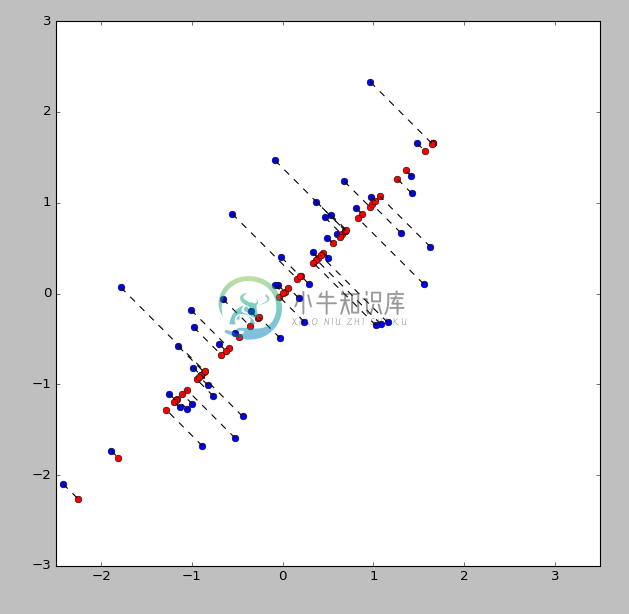
2维数据降为1维
要投影的方向
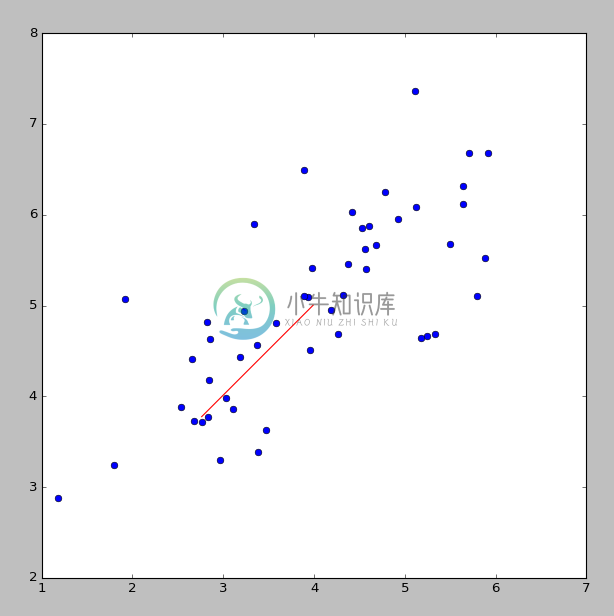
2D降为1D及对应关系
人脸数据降维
原始数据

可视化部分 U 矩阵信息

恢复数据

9、使用 scikit-learn 库中的 PCA 实现降维
导入需要的包:
#-*- coding: utf-8 -*-
# Author:bob
# Date:2016.12.22
import numpy as np
from matplotlib import pyplot as plt
from scipy import io as spio
from sklearn.decomposition import pca
from sklearn.preprocessing import StandardScaler
归一化数据
'''归一化数据并作图'''
scaler = StandardScaler()
scaler.fit(X)
x_train = scaler.transform(X)
使用PCA模型拟合数据,并降维
n_components 对应要将的维度
'''拟合数据'''
K=1 # 要降的维度
model = pca.PCA(n_components=K).fit(x_train) # 拟合数据,n_components定义要降的维度
Z = model.transform(x_train) # transform就会执行降维操作
数据恢复
model.components_ 会得到降维使用的 U 矩阵
'''数据恢复并作图'''
Ureduce = model.components_ # 得到降维用的Ureduce
x_rec = np.dot(Z,Ureduce) # 数据恢复

