递归
阶乘
可以用循环的方法,即从1开始,乘2,再乘3…..一直乘到n。这种方法容易理解,也容易实现
由于n! = n× (n-1)! 数学里定义0!=1,从而n!可以用下面的递归公式表示:
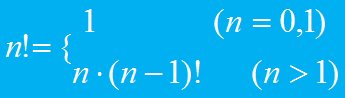
int p(int n){
if(n == 0){
return 1;
}else{
return n*p(n-1);
}
}
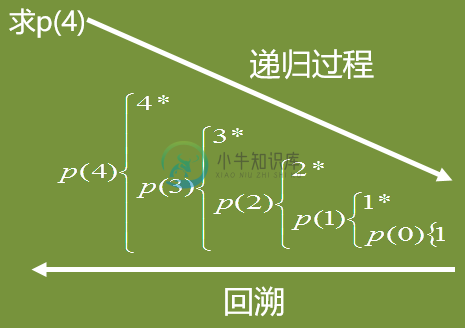
递归的执行过程
递归与迭代的选择:
- 对于大多数常用的递归都有简单、等价的迭代程序。究竟使用哪一种,凭你的经验选择。
- 迭代程序复杂,但效率高。
- 递归程序逻辑清晰,但往往效率较低。
斐波那契数列
兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有兔都不死,那么一年以后可以繁殖多少对兔子?
int f(int n){
if(n==0){
return 0;
}else if(n==1){
return 1;
}else{
return (f(n-1)+f(n-2));
}
}
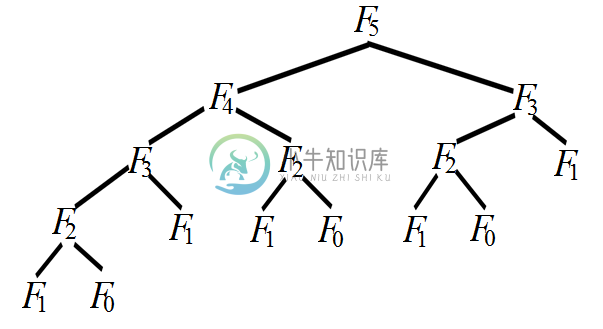
实现效率分析:消费的时间是灾难性的!!!
Fibonacci函数的迭代实现
int f(int n)
{ int i, fn, fn_1 = 0, fn_2 = 1;
if (n == 0) return 0;
if (n == 1) return 1;
for ( i = 2; i<=n; ++i)
{ fn = fn_1 + fn_2;
fn_2 = fn_1; fn_1 = fn; }
return fn;
}
消耗的时间:执行n次加法和3n次赋值!!!
系统考虑:对递归函数的每次调用都需要内存空间。由于很多调用的活动都是同时进行的,操作系统可能会耗尽可用的内存,避免在处理过大的n时产生溢出问题。
数字旋转方阵(蛇阵)
数字旋转方阵如图所示。编程输出任意N*N的蛇阵。

用递归的观点看问题
- 先填最外圈,然后再填内部内部的填法同上。也是先填最外圈,再填内部。
- 根据上述思想,可以设计一个递归函数fill。该函数先填外圈,然后递归调用自己填内部。
函数原型:
void fill(int number, int begin, int size)
// number:表示要填入的起始数据
// begin:表示要填的起始位置
// size:蛇阵的规模
要生成一个6*6的蛇阵只要调用:fill(1,0,6)
#include<iostream>
using namespace std;
int p[20][20];
void fill( int, int, int );
int main()
{
int row, col, size;
cout << "请输入蛇阵的规模:";
cin >> size;
fill( 1, 0, size );
for ( row = 0; row < size; row++ )
{
cout << endl;
for ( col = 0; col < size; col++ ){
cout << p[row][col] << '\t';
}
}
return 0;
}
void fill( int number, int begin, int size )
{
int i, row = begin, col = begin;
if ( size == 0 ) return;
if ( size == 1 )
{
p[begin][begin] = number;
return;
}
p[row][col] = number++;
for ( i = 0; i < size - 1; i++ )
{
p[++row][col] = number++;
}
for ( i = 0; i < size - 1; i++ )
{
p[row][++col] = number++;
}
for ( i = 0; i < size - 1; i++ )
{
p[--row][col] = number++;
}
for ( i = 0; i < size - 2; i++ )
{
p[row][--col] = number++;
}
fill( number, begin + 1, size - 2 );
}
- 自上而下填最左列
- 自左而右填最下行
- 自下而上填最右列
- 自右而左填最上行
- 递归调用fill,规模减2,起始位置为原来的下一行下一列,填入的起始数字为填入一圈后的第一个数字。
汉诺塔问题
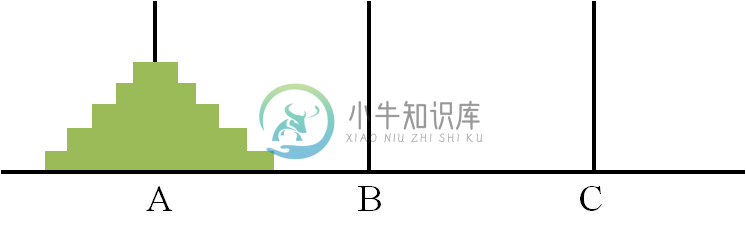
目标:将A上的盘子全部移到B上
规则:每次只能移动一个盘子;不允许大盘子放在小盘子上
解题思路:
- 最简单的情况,只有一个盘子:将盘子直接从A移到B
- 大于一个盘子的情况:
- 将除了最下面一个盘子外的所有盘子从A移到C
- 将最下面的盘子从A移到B
- 将C上的盘子移回B
void Hanoi(int n, char start, char finish, char temp){
if (n==1){
cout << start << "->" << finish << '\t';
}else {
Hanoi(n-1, start, temp, finish);
cout << start << "->" << finish << '\t';
Hanoi(n-1, temp, finish, start);
}
}
基于递归的算法
- 回溯法
- 分治法
- 动态规则
回溯法
- 首先暂时放弃问题规模大小的限制,并将问题的候选解按某种顺序逐一枚举和检验。当发现候选解不可能是解时,就选择下一候选解。如果当前候选解除了不满足规模要求外,满足其他所有要求时,继续扩大当前候选解的规模,并继续试探。如果当前的候选解满足包括问题规模在内的所有要求时,该候选解就是问题的一个解。
- 寻找下一候选解的过程称为回朔。
- 扩大当前候选解的规模,并继续试探的过程称为向前试探。
- 分书问题和八皇后都是典型的回溯法问题
实例:分书问题
有编号为0,1,2,3,4的5本书,准备分给5个人A,B,C,D,E,每个人的阅读兴趣用一个二维数组描述:
- Like[i][j] = true i喜欢书j
- Like[i][j] = false i不喜欢书j
写一个程序,输出所有皆大欢喜的分书方案
存储设计:
- 用一个二维数组like存储用户的兴趣
- take[i] = j表示第i本书分给了第j个人。如果第i本书尚未被分配,给take[i]一个特殊值,如-1。

解题思路:
设计一个函数trynext(i)给第i个人分书。
依次尝试把书j分给人i。
如果第i个人不喜欢第j本书,则尝试下一本书,如果喜欢,并且第j本书尚未分配,则把书j分配给i。
如果i是最后一个人,则方案数加1,输出该方案。否则调用trynext(i+1)为第i+1个人分书。
回溯。让第i个人退回书j,尝试下一个j,即寻找下一个可行的方案
- 由于在每次try中都要用到like,take以及目前找到的方案数n,因此可将它们作为全局变量,以免每次函数调用时都要带一大串参数。
void trynext(int i)
{
int j, k;
for (j=0; j<5; ++j) {
if (like[i][j] && take[j]== -1) { //如果i喜欢j,并且j未被分配
take[j] = i; //j分给i
if (i == 4) { //找到一种新方案,输出此方案
n++;
cout << "\n第" << n << "种方案: "<< endl;
cout << " 书\t人" << endl;
for (k=0; k<5; k++)
cout <<k << '\t' << char(take[k] +'A') << endl;
}
else trynext(i+1); //为下一个人分书
take[j] = -1; //尝试找下一方案
}
}
}
当like矩阵的值为:

调用trynext(0);的结果为:
| 书 | 人(方案1) | 人(方案2) |
|---|---|---|
| 0 | B | B |
| 1 | C | E |
| 2 | A | A |
| 3 | D | D |
| 4 | E | C |
实例:八皇后问题
在一个8*8的棋盘上放8个皇后,使8个皇后中没有两个以上的皇后会在同一行、同一列或同一对角线上。
八皇后问题的求解过程:
求解过程从空配置开始,在第一列到第m列为合理配置的基础上再配置m+1列,直到第n列的配置也时合理时,就找到了一个解。另外在一列上也有n种配置。开始时配置在第一行,以后改变时,顺序选择第二行、第三行 ...... 第n行。当配置到第n行时还找不到一个合理的配置时,就要回朔,去改变前一列的配置。
queen_all(k)
{ for (i = 1; i <=8; ++i)
if (皇后放在第i行是可行的) {
在第i行放入皇后;
if(k == 8) 输出解;
else queen_all(k+1);
恢复该位置为空;
}
}
棋盘的数据结构的设计:
- 比较直观的方法是采用一个二维数组,但仔细考察,就会发现,这种表示方法给调整候选解及检查其合理性会带来困难。
- 对于本题来说,我们关心的并不是皇后的具体位置,而是“一个皇后是否已经在某行和某条斜线合理地安置好了”。
- 因为在每一列上恰好放一个皇后,所以引入一个一维数组(设为col(9)),值col[j]表示在棋盘第j列上的皇后位置。如col[3]的值为4,就表示第三列的皇后在第四行。另外,为了使程序在找完了全部解后回溯到最初位置,设定col[0]的初值为0。当回溯到第0列时,说明程序已求得全部解(或无解),结束程序执行。
候选解的合理性检查:引入以下三个工作数组
- 数组a[9],a[A]=true表示第A行上还没有皇后;
- 数组b[16],b[A]=true表示第A条右高左低斜线上没有皇后;从左上角依次编到右下角(1-15)。
- 数组c[16],c[A]=true表示第A条左高右低斜线上没有皇后。从左下角依次编到右上角(1-15)。
void queen_a11(int k) //在8x8棋盘的第k列上找合理的配置
{int i, j;
char awn;
for(i = 1; i < 9; i++) // 依次在l至8行上配置k列的皇后
if ( a[i] && b[k+i-1] && c[8+k-i]) { //可行位置
col[k] = i;
a[i] = b[k+i-1] = c[8+k-i] = false; //置对应位置有皇后
if (k == 8) { // 找到一个可行解
for (j = 1; j <= 8; j++) cout << j << col[j]<< '\t' ;
cout << endl;
cin >> awn;
if (awn=='Q' || awn=='q') exit(0);
}
else queen_a11(k+1); //递归至第k+1列
a[i] = b[k+i-1] = c[8+k-i] = true; //恢复对应位置无皇后
}
}
主程序
int col[9];
bool a[9], b[17],c[17];
int main()
{ int j;
for(j = 0; j <=8; j++) a[j] = true;
for(j = 0; j <= 16; j++) b[j] = c[j] = true;
queen_a11(1);
return 0;
}
实例:迷宫问题
迷宫问题是关于程序设计的一个典型问题,现在用递归的方法来求解迷宫问题。
所谓迷宫问题就是把一只老鼠从无顶盖的大盒子(迷宫)的入口处赶进迷宫。迷宫中设置了很多墙壁,对前进方向形成了多处障碍。在迷宫的唯一出口处放置了一块奶酪,吸引老鼠在迷宫中寻找通路以到达出口。
如果从迷宫的入口到达出口,途中不出现行进方向错误,则得到一条最佳路线。利用递归方法可获得迷宫从入口到出口的最佳路线。
用一个二维数组maze[m+2][p+2]来表示迷宫。如图所示,当数组元素maze[i][j]=1时,表示该位置是墙壁,不能通行;当maze[i][j]=0时,表示该位置是通路。1≤i≤m,1≤j≤p。
数组的第0行、第m+1行,以及第0列和第p+1列是迷宫的围墙,第0列、p+1列中各有一个0,表示迷宫的入口和出口。

在求解迷宫问题的过程中,采用回溯法。老鼠在迷宫中任一时刻的位置可用数组行下标i和列下标j表示。从maze[i][j]出发,可能的前进方向有8个,按顺时针方向为N([i-1][j]),NE([i-1][j+1]),E([i][j+1]),SE([i+1][j+1]),S([i+1][j]),SW([i+1][j-1]),W([i][j-1]),NW([i-1][j-1])
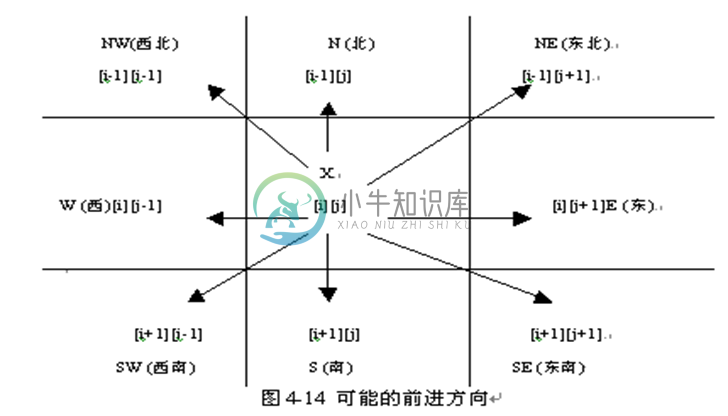
设位置[i][j]标记为X,它实际是一个交通路口。X周围有8个前进方向,分别代表8个前进位置。如果某一方向是0值,表示该方向有路可通,否则表示该方向已堵死。
为了有效地选择下一位置,可以将从位置[i][j]出发可能的前进方向预先定义在一个表内,参看表4-6。该表为前进方向表,它给出向各个方向的偏移量。
- 前进方向表move
| move[q].dir | move[q].a | move[q].b | move[q].dir | move[q].a | move[q].b |
|---|---|---|---|---|---|
| "N" | 1 | 0 | "S" | 1 | 0 |
| "NE" | 1 | 1 | "SW" | 1 | 1 |
| "E" | 0 | 1 | "W" | 0 | 1 |
| "SE" | 1 | 1 | "NW" | 1 | 1 |
struct offsets { //位置在直角坐标系下的偏移
int a, b; //a,b是x,y方向的偏移
char * dir; //dir是方向
};
offsets move[8]; //各个方向的偏移表
例如,当前位置在[i][j]时,若向西南(SW)方向走,下一相邻位置[g][h]则为: g = i + move[5].a = i+1; h = j + move[5].b = j-1; d = move[5].dir;
当在迷宫中向前试探时,可根据表4-6所示的前进方向表,选择某一个前进方向向前试探。如果该前进方向走不通,则在前进路径上回退一步,再尝试其他的允许方向。
为了防止重走原路,另外设置一个标志矩阵mark[m+2][p+2],它的所有元素都初始化为0。一旦行进到迷宫的某个位置[i][j],则将mark[i][j]置为1。下次这个位置不能再走了。
解决迷宫问题的递归算法
// 从迷宫某一位置[i][j]开始,寻找通向出口[m][p]的一条路径。
// 如果找到,则函数返回1。否则函数返回0。试探的出发点为[1][1]
int seekpath (int x, int y){
int i, g, h; //用g,h记录位置信息
char * d; //用d记录方向
if (x == m && y == p) return 1; //已到达出口,返回1
for (i = 0; i<8; i++){ //依次对每一个方向寻找通向出口的路径
g = x+move[i].a;
h = y+move[i].b;
d = move[i].dir; //找下一个位置和方向(g,h,dir)
if (maze[g][h] == 0 && mark[g][h] == 0) // 下一位置可通,试探该方向
{
mark[g][h] = 1; //标记为已访问过
if (seekpath (g , h))
{ //从此位置递归试探
cout<<"("<<g<<","<<h<<"),"<<"Direction"<<dir<<",";
return 1; //试探成功,逆向输出路径坐标
}
}
//回溯,换一个方向再试探通向出口的路径
}
if (x == 1 && y == 1) cout<<"no path in maze"<<endl;
return 0;
}
分治法:递归与分而治之法
- 分:分成较小的可以递归解决的问题
- 治:从子问题的解形成原始问题的解
- 分而治之算法通常都是高效的递归算法
- 在分而治之法中,递归是“分”,额外的开销是“治”
最大连续子序列问题
给定(可能是负的)整数序列A1 , A2 , ... An,寻找(并标识) $\sum_{k=i}^{j}A_k$ 的值为最大的序列。如果所有的整数都是负的,那么最大连续子序列的和是零。
例如,假设输入是{-2, 11, -4, 13, -5, 2},那么答案是20,它表示连续子序列包含了第2项到第4项(如粗体字部分)。又如第二个例子,对于输入{1, -3, 4, -2, -1, 6},答案是7,这个子序列包含最后四项。
分而治之法的解题思路:
假设输入是{4,-3,5,-2,-1,2,6,-2}。我们把这个输入划分成两部分,前四个和后四个。这样最大连续子序列的和可能出现在下面三种情况中。
- 情况1:整个位于前半部,可递归计算。
- 情况2:整个位于后半部,可递归计算。
- 情况3:从前半部开始但在后半部结束。
情况3的解决方法:
从两半部分的边界开始,通过从右到左的扫描来找到左半段的最长序列。类似地,从左到右的扫描找到右半段的最长序列。把这两个子序列组合起来,形成跨越分割边界的最大连续子序列。
在这个实例中,结果序列是从第一部分的第一个元素到第二部分的其余元素。总和是两个子序列的和,即4+7=11。
算法总结:
- 递归地计算整个位于前半部的最大连续子序列。
- 递归地计算整个位于后半部的最大连续子序列。
- 通过两个连续循环,计算从前半部开始但在后半部结束的最大连续子序列的和。
- 选择三个和中的最大值。
// 找出数组a的下标从left到right之间的和值最大的子序列
// 用法:maxsum(a, 0, n-1);
int maxSum(int a[ ], int left, int right )
{ // maxLeft和maxRight分别为左、右半部的最长子序列和
int maxLeft, maxRight, center;
int leftSum = 0, rightSum = 0;
int maxLeftTmp = NEGMAX, maxRightTmp = NEGMAX; // NEGMAX最大负整数
if (left == right) return a[left] > 0 ? a[left] : 0;
center = (left + right) / 2;
maxLeft = maxSum(a, left, center); // 找前半部分的最大连续子序列
maxRight = maxSum(a, center + 1, right); // 找后半部分的最大连续子序列
//找从前半部分开始到后半部分结束的最大连续子序列
for (int i = center; i >= left; --i){
leftSum += a[i];
if (leftSum > maxLeftTmp) maxLeftTmp = leftSum;
}
for (i = center + 1; i <= right; ++i){
rightSum += a[i];
if (rightSum > maxRightTmp) maxRightTmp = rightSum;
}
return max3(maxLeft, maxRight, maxLeftTmp + maxRightTmp);
}
动态规划
在实际中经常会遇到一个复杂的问题不能简单地分成几个子问题,而是会分解出一系列的子问题。如果用分治法的话会使得递归调用的次数呈指数增长。如Finonacci数列的计算,第i个Fibonacci数是前两个Fibonacci数之和。
它是基于分而治之算法。在每一阶段都将当前问题分解为多个已解决的子问题
为解决递归爆炸问题,通常先找出小问题的解,记录在一个表中,在解决大问题时不需要递归,只需要从表中取出小问题的解。
实例:找零问题
对于一种货币,有面值为C1, C2, …, CN(分)的硬币,最少需要多少个硬币来找出K分钱的零钱。
贪婪法解法
我们不断使用可能的最大面值的硬币。如:硬币有1、5、10和25分的面值。我们可以通过使用2个25分、一个10分的硬币以及三个1分来找出63分钱,一共是6个硬币。 如果包含一个21分硬币时,贪心算法仍然给出一个用六个硬币的解,但是最佳的解是用三个硬币(三个都是21分的硬币。)
解法1:分治法
如果我们可以用一个硬币找零,这就是最小的。否则,对于每个可能的值i,我们可以独立计算找i分钱零钱和K-i分钱需要的最小硬币数。然后选择这个和最小的i。
怎样找出63分钱零钱
- 找出1分钱零钱和62分钱零钱分别需要的硬币数是1和4。因此,63分钱需要使用五个硬币。
- 找出2分钱和61分钱分别需要2和4个硬币,一共是六个硬币。
- 我们继续尝试所有的可能性。我们看到一个21分和42分的分解,它可以分别用一个和两个硬币来找开,因此,这个找零问题就可以用三个硬币解决。
- 我们需要尝试的最后一种分解是31分和32分。我们可以用两个硬币找出31分零钱,用三个硬币找出32分零钱,一共是五个硬币。
- 因此最小值是三个硬币。
int coin(int k)
{
int i, tmp, int coinNum = k;
if (能用一个硬币找零) return 1;
for (i=1; i<k; ++i)
if ((tmp = coin(i) + coin(k-i)) < coinNum)
coinNum = tmp;
return coinNum;
}
上述解法分析:此算法的效率很低。事实上63分钱找零的问题是不会在一个合理的时间内解决的。就如Finbonacci 函数一样
解法2
- 通过指定其中的一个硬币来递归地简化问题。
- 例如,对于63分钱,我们可以给出以下找零的办法。
- 一个1分的硬币加上递归地分派62分钱
- 一个5分的硬币加上递归地分派58分钱
- 一个10分的硬币加上递归地分派53分钱
- 一个21分的硬币加上递归地分派42分钱
- 一个25分的硬币加上递归地分派38分钱
- 该算法的问题仍然是效率问题
动态规划解
效率低下主要是由于重复计算造成的。因此,可把已有子问题的答案存放起来,当再次遇到此子问题时就不用重复计算了。在本例中,我们用coinsUsed[i]代表了找i分零钱所需的最小硬币数。
算法思想
- 先找出0分钱的找零方法,把最小硬币数存入coinUsed[0]
- 依次找出1分钱、2分钱…的找零方法,知道到达要找零的钱为止:
- 对每个要找的零钱i,可以把i分解成某个coins[j]和 i - coins[j],
- 所需硬币数为coinUsed[i-coins[j]]+1。对所有的j,取最小的coinUsed[i-coins[j]]+1作为i元钱找零的的答案。
// coins存放所有不同的硬币值,不同的硬币个数为differentCoins
// maxChange为要找的零钱数
void makechange( int coins[ ], int differentCoins,
int maxChange, int coinUsed[] )
{
coinUsed[0] = 0;
for (int cents = 1; cents <= maxChange; cents++) {
int minCoins = cents;
for (int j = 1; j < differentCoins; j++) {
if (coins[j] > cents) continue;
if (coinUsed[ cents - coins[j] ] + 1 < minCoins)
minCoins = coinUsed[ cents - coins[j] ] + 1;
}
coinUsed[cents] = minCoins;
}
}
递归调戏GoogleEarth
#include <stdio.h>
#include <stdlib.h>
#include <Windows.h>
//01.HWND类型的变量介绍:
// 1.窗体的唯一标识号
// 2.全局变量,谁都可以进行访问,递归函数同样可以调用
HWND win;
//打开GoogleEarth
void openGoogleEarth()
{
ShellExecuteA(0, "open", "\"C:\\Program Files (x86)\\Google\\Google Earth\\client\\googleearth.exe\"", 0, 0, 1);
}
//GoogleEarth窗体的隐藏和显示切换
void HSGoogleEarth()
{//死循环-->反复调用-->递归的形式-->递归函数
ShowWindow(win, SW_HIDE);//隐藏
Sleep(1000);
ShowWindow(win, SW_SHOW);//显示
Sleep(1000);//实现完美间隔形式需要这行代码
HSGoogleEarth();
}
//Google浏览器窗体的从左往右移动
void moveGoogleEarth(int n)
{//递归函数
if (1600 == n)//当n == 1600的时候,结束递归循环
{
return;//跳出递归循环,进行递归函数的弹栈操作
}
else
{
SetWindowPos(win, NULL, n, 0, 500, 500, 0);//设置窗体坐标,尺寸
Sleep(50);//休眠当前处理本函数的线程
n += 10;//让递归循环函数趋于终止的条件
}
moveGoogleEarth(n);//递归调用
}
//0~1600,长度,宽度都会改变,放大
void googleEarthSmallToBig(int n)
{
if (1600 == n)
{
return;//跳出递归循环结构
}
else
{
//实现从小到大,GoogleEarth有一个最小的窗口比例,最小不能小于这个窗口比例
SetWindowPos(win, NULL, 0, 0, n, n * 768 / 1366, 0);//设置窗体坐标,尺寸
Sleep(50);//休眠
n += 10;
}
googleEarthSmallToBig(n);
}
//关闭GoogleEarth
void closeGoogleEarth()
{
system("taskkill /f /im googleearth.exe");
}
//玩儿弄GoogleEarth
void playGoogleEarth()
{
//寻找GoogleEarth窗体本身
win = FindWindowA("QWidget", "Google Earth");
if (NULL == win)
{
printf("GoogleEarth正在玩失踪! \n");
return;
}
Sleep(2000);
SetWindowTextA(win, "拉里佩奇!你的产品好垃圾! \n");
Sleep(2000);
moveGoogleEarth(0);//移动
googleEarthSmallToBig(0);//放大
HSGoogleEarth();//显示隐藏切换
}
int main01(void)
{
closeGoogleEarth();
Sleep(2000);
openGoogleEarth();
Sleep(5000);
playGoogleEarth();
system("pause");
}

