数据存储的原理
进制转换
十进制转换为二进制
十进制转换成二进制可以采用除2取余的方式,也就是说将要转换的数,先除以2,获得商和余数,将商继续除以2,获得商和余数,此过程一直重复直到商为0。最后将所有得到的余数倒序排列,即可得到转换结果。
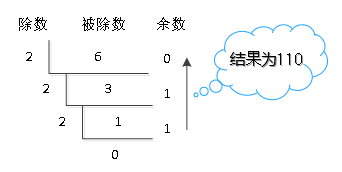
二进制转换为十进制
二进制转化成十进制要从右到左用二进制位上的每个数去乘以2的相应次方。
以二进制数1101为例,将其转换为十进制形式,转换方式如下:

二进制转换为八进制
二进制转换为八进制,有一个技巧,就是将二进制数自右向左每三位分成一段(若不足三位,左边用0补齐),然后将二进制每段的三位转为八进制的一位,转换过程中数值的对应关系如下表所示。
| 二进制 | 八进制 |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
二进制转换为八进制
以00101010转换为八进制,具体演算过程如下。
- 每三位分成一段,结果为:000 101 010
- 将每段的数值分别查表替换,结果如下
010 → 2
101 → 5
000 → 0
- 将替换的结果进行组合,组合后的八进制为0052
十六进制转换为八进制
将二进制转为十六进制时,将二进制数每四位分成一段(若不足4位用0补齐),再查表转换即可。二进制转十六进制过程中数值的对应关系如下表所示。
| 二进制 | 十六进制 | 二进制 | 十六进制 | |
|---|---|---|---|---|
| 0000 | 0 | 1000 | 8 | |
| 0001 | 1 | 1001 | 9 | |
| 0010 | 2 | 1010 | A | |
| 0011 | 3 | 1011 | B | |
| 0100 | 4 | 1100 | C | |
| 0101 | 5 | 1101 | D | |
| 0110 | 6 | 1110 | E | |
| 0111 | 7 | 1111 | F |
案例实现
十进制的100转换成二进制
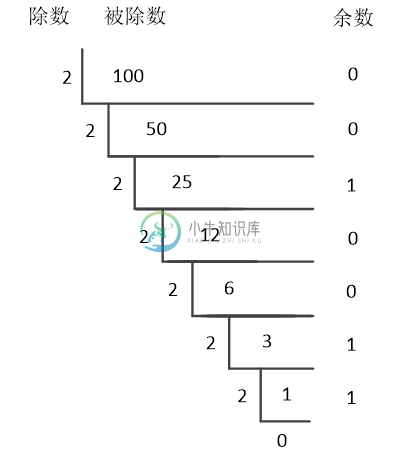
小数二进制
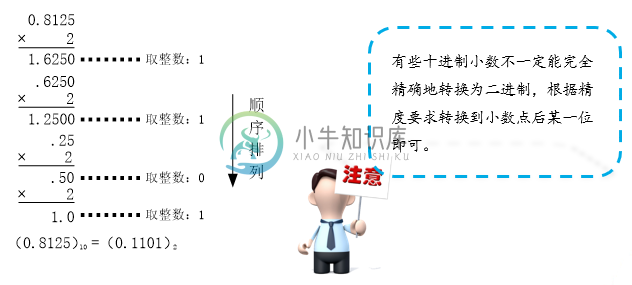
十进制小数转换为二进制采用“乘2取整”的方式。方法是用2乘以十进制小数部分,将结果中的整数部分去掉,再次用2乘以余下的小数部分,并去掉其结果的整数部分;如此继续下去,直到余下的小数部分为0或满足所要求的精度为止。最后将每次得到的整数部分(0或1)按先后顺序排列,即为小数对应的二进制。
浮点型数据在内存中的存储方式
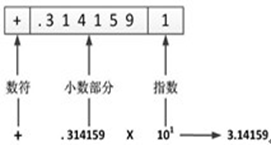
浮点数包含符号位、小数位和指数位三部分。例如,小数3.14159在内存中的符号位为“+”,小数部分为.31415,指数位为1,连方式接在一起即为 “+0.314159 * 101 = 3.14159”。
在C语言中,一个小数会被默认为double类型的值,因此在为一个float类型的变量赋值时需要注意一点,所赋值的后面一定要加上字母“F”(或者小写“f”),而为double类型的变量赋值时,其所赋值后面的字符“D”(或小写“d”),可以省略。
补码
正数:原码 = 反码 = 补码,负数:反码 = 原码取反,补码 = 原码取反加1
负数以补码的形式在计算机中存储
#include<stdio.h>
#include<stdlib.h>
void main3()
{
//printf不会进行数据类型转换
printf("%d", (int)10.3);//printf不管你是什么类型,按照%d ,%f解析数据
printf("\n%f", (float)10);
getchar();
}
void main4()
{
int num = 100;
printf("%p", &num);//不同的解释方式就有不同的解释结果
getchar();
}
void main5()
{
char ch = 1,ch1='1';//字符与编号的区别
printf("%d,%d", ch,ch1);
getchar();
}
void main6()
{
//解析的时候,与数据的长度有关系
unsigned short num = 65535+1;
printf("刘宁波有%d元", num);
// 99
// 100
getchar();
}
void main7()
{
//补码,计算机存储数据的方式
short num = -1;
printf("%d", num);
printf("\n%u", num);//%u 0-正整数
getchar();
}
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
//01.负数不能采用无符号类型的变量进行存储:
// 1.会造成数据被解析的过大
// 2.无符号类型的变量只能存储正数
// 负数的二进制通常很大,因为以1作为开头
// 所以存储的时候不能用无符号进行存储
// 否则存储的数据实体过大
int main01(void)
{
unsigned int num = -1;//1111 1111 1111 1111 1111 1111 1111 1111
printf("%u", num);
for (int i = 0; i < num; i++)
{//循环10次
printf("你好天朝! \n");
}
system("pause");
return 1;
}
//02.计算机当中的整数存储原理:
// 1.所有的整数都采用补码存储
// 2.原码-->反码-->补码:
// 正整数的原码,反码,补码一致
// 负整数的原码,反码,补码特点:
// 原码:该负数所对应的正整数的原码最高位加符号位(1)
// 反码:该负数所对应的原码的符号位不变,其余为取反
// 补码:该负数所对应的反码+1
// 3.采用补码的优点:
// 提升运算效率,减少不必要的计算操作
// 将以前的多步骤运算进行精简
// 例如:统一了+-法的差异,全部采用加法,符号位转到补码的表示当中
// 举例:1-1-2-2<==>1+(-1)+(-2)+(-3)-->统一为加法运算法则
int main02(void)
{
char ch = -17;//计算机都是补码存储,手机,电脑,服务器也同样采用补码进行整数的存储
//0001 0001 +17的原码
//1001 0001 -17的原码
//1111 1110 -17的反码
//1111 1111 -17的补码 EF-->十六进制
printf("%p \n", &ch);
system("pause");
return 1;
}
//03.有符号和无符号的推理法则:
// 1.-1所对应的内存二进制数据是:
// 1111 1111 1111 1111 1111 1111 1111 1111
// 2.对内存二进制数据的解析方式:
// %d:按照有符号的解析法则(负数倒推)
// 补码-->反码-->原码-->负数
// 例如:-1的补码
// 1111 1111 补码
// 1111 1110 反码
// 1000 0001 原码-->就是-1
// %u:按照无符号的解析法则(整数倒推)
// 补码=原码-->证书
// 1111 1111-->就是255
int main03(void)
{
int num = -1;
//0000 0000 0000 0000 0000 0000 0000 0001 +1原码
//1000 0000 0000 0000 0000 0000 0000 0001 - 1原码
//1111 1111 1111 1111 1111 1111 1111 1110 - 1反码
//1111 1111 1111 1111 1111 1111 1111 1111 - 1补码
printf("%d \n", num);
printf("%u \n", num);
system("pause");
return 1;
}
int main04(void)
{
printf("INT_MIN = %d, INT_MAX = %d \n", INT_MIN, INT_MAX);
system("pause");
return 1;
}
//04.特殊数据的二进制数值:
// -1的内存二进制数据全是1
// 按照有符号解析得出-1
// 按照无符号解析就是一个整数最大值
// 越界现象解释:
// 物极必反的二进制数据转换特点
int main05(void)
{
int num = -1;
unsigned int data = 42949697295u;//无符号数据 1111 1111 1111 1111 1111 1111 1111 1111全部的是数据,并且按照正整数的方式进行解析
int num1 = 4294967295u;//等价于32个二进制的1
unsigned int data1 = -1;//等价于32个二进制的1
printf("%d \n", num);//-1
printf("%u \n", num);//4294967295
printf("%d \n", num1);//-1
printf("%u \n", num1);//4294967295
printf("%u \n", data);//4294967295
printf("%d \n", data);//-1
printf("%u \n", data1);//4294967295
printf("%d \n", data1);//-1
printf("%f \n", 1);//printf,不管三七二十一,抓区二进制数据就解析
system("pause");
return 1;
}
int main06(void)
{
printf("INT_MIN = %d, INT_MAX = %d \n", INT_MIN, INT_MAX);
printf("INT_MIN = %d, INT_MAX + 1 = %d \n", INT_MIN, INT_MAX + 1);
printf("INT_MIN - 1 = %d, INT_MAX = %d \n", INT_MIN - 1, INT_MAX);
printf("UINT_MIN = %d, UINT_MAX = %d \n", 0, UINT_MAX);
printf("UINT_MIN = %d, UINT_MAX + 1 = %d \n", 0, UINT_MAX + 1);
printf("UINT_MIN - 1 =%d, UINT_MAX = %d \n", 0 - 1, UINT_MAX);
system("pause");
return 1;
}
计算机补码原理
#include<stdio.h>
#include<stdlib.h>
#include<limits.h>
void main10()
{
int x = 1;
int y = -1;//补码
printf("x=%p,y=%p", &x, &y);
system("pause");
}
void main123()
{
//int unsigned int 4个字节32位
//有符号,0代表正数,1代表负数
//0111 1111 1111 1111 1111 1111 1111 1111
//1111 1111 1111 1111 1111 1111 1111 1111//无符号,正数,全部都是数据
printf("%d,%d", INT_MAX, INT_MIN);//%d只能显示INT_MIN->INT_MAX
printf("\n%d,%d", INT_MAX+1, INT_MIN-1);
printf("\n%u,%u", UINT_MAX, 0);
printf("\n%u,%u", UINT_MAX+1, 0-1);//%u 0->UINT_MAX
system("pause");
}
void main1234()
{
int x = 4294967295;
int y = -1;
//1111 1111 1111 1111 1111 1111 1111 1111内存的存储方式
//无符号,没有符号位,全部都是数据 4294967295
//0000 0000 0000 0000 0000 0000 0000 0001 1原码
//1000 0000 0000 0000 0000 0000 0000 0001 -1的原码
//1111 1111 1111 1111 1111 1111 1111 1110 -1的反码
//1111 1111 1111 1111 1111 1111 1111 1111 -1的补码
printf("%d,%u", x,x);
printf("\n%d,%u", y, y);
getchar();
}
void main()
{
unsigned int num = -1;
//1111 1111 1111 1111 1111 1111 1111 1111内存的存储方式
printf("%d,%u", num, num);
system("pause");
}

