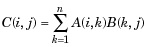Show 例子 1
MATLAB允许两种不同类型的算术运算 -
- 矩阵算术运算
- 数组算术运算
矩阵算术运算与线性代数中定义的相同。 数组操作在一维和多维数组上逐个元素地执行。
矩阵运算符和数组运算符由句点(。)符号区分。 但是,由于矩阵和数组的加法和减法操作相同,因此两种情况下的运算符相同。
下表给出了运算符的简要说明 -
| Sr.No. | 操作符和说明 |
|---|---|
| 1 | + 加或一元加。 A + B添加存储在变量A和B中的值.A和B必须具有相同的大小,除非一个是标量。 标量可以添加到任何大小的矩阵中。 |
| 2 | - 减法或一元减号。 AB从A中减去B的值.A和B必须具有相同的大小,除非一个是标量。 可以从任何大小的矩阵中减去标量。 |
| 3 | * 矩阵乘法。 C = A * B是矩阵A和B的线性代数乘积。更准确地说,
对于非标量A和B,A的列数必须等于B的行数。标量可以乘以任意大小的矩阵。 |
| 4 | .* 数组乘法。 A. * B是数组A和B的逐元素乘积.A和B必须具有相同的大小,除非其中一个是标量。 |
| 5 | / 斜线或矩阵右划分。 B/A与B * inv(A)大致相同。 更准确地说,B/A =(A'\ B')'。 |
| 6 | ./ 数组右分裂。 A./B是具有元素A(i,j)/ B(i,j)的矩阵。 A和B必须具有相同的大小,除非其中一个是标量。 |
| 7 | \ 反斜杠或矩阵左分裂。 如果A是方阵,则A\B与inv(A)* B大致相同,除非它以不同的方式计算。 如果A是n×n矩阵,B是具有n个分量的列向量,或者是具有多个这样的列的矩阵,则X = A\B是等式AX = B的解。 如果A严重缩放或几乎是单数,则会显示警告消息。 |
| 8 | .\ 数组左分裂。 A.\B是具有元素B(i,j)/ A(i,j)的矩阵。 A和B必须具有相同的大小,除非其中一个是标量。 |
| 9 | ^ 矩阵功率。 如果p是标量,则X ^ p是幂p的X. 如果p是整数,则通过重复平方来计算功率。 如果整数为负,则首先反转X. 对于p的其他值,计算涉及特征值和特征向量,使得如果[V,D] = eig(X),则X ^ p = V * D. ^ p/V. |
| 10 | .^ 阵列功率。 A. ^ B是具有元素A(i,j)到B(i,j)幂的矩阵。 A和B必须具有相同的大小,除非其中一个是标量。 |
| 11 | ' 矩阵转置。 A'是A的线性代数转置。对于复数矩阵,这是复共轭转置。 |
| 12 | .' 数组转置。 一个。' 是A的数组转置。对于复数矩阵,这不涉及共轭。 |
例子 (Example)
以下示例显示了算术运算符在标量数据上的使用。 使用以下代码创建脚本文件 -
a = 10;
b = 20;
c = a + b
d = a - b
e = a * b
f = a/b
g = a\b
x = 7;
y = 3;
z = x ^ y
运行该文件时,它会产生以下结果 -
c = 30
d = -10
e = 200
f = 0.50000
g = 2
z = 343
算术运算的函数
除上述算术运算符外,MATLAB还提供以下用于类似目的的命令/函数 -
| Sr.No. | 功能说明 |
|---|---|
| 1 | uplus(a) 一元加; 增加数量a |
| 2 | plus (a,b) 加; 返回a + b |
| 3 | uminus(a) 一元减去; 减去金额a |
| 4 | minus(a, b) 减去; 返回a - b |
| 5 | times(a, b) 数组乘法; 返回a。* b |
| 6 | mtimes(a, b) 矩阵乘法; 返回a * b |
| 7 | rdivide(a, b) 右阵列划分; 返回./ b |
| 8 | ldivide(a, b) 左阵列划分; 返回一个。\ b |
| 9 | mrdivide(A, B) 求解x的线性方程组xA = B |
| 10 | mldivide(A, B) 求解x的线性方程组Ax = B |
| 11 | power(a, b) 阵列功率; 返回一个。^ b |
| 12 | mpower(a, b) 矩阵功率; 返回a ^ b |
| 13 | cumprod(A) 累积产品; 返回与包含累积产品的数组A大小相同的数组。
|
| 14 | cumprod(A, dim) 返回维度dim的累积产品。 |
| 15 | cumsum(A) 累计金额; 返回包含累积和的数组A.
|
| 16 | cumsum(A, dim) 返回维度dim元素的累积和。 |
| 17 | diff(X) 差异和近似导数; 计算X的相邻元素之间的差异。
|
| 18 | diff(X,n) 递归地应用diff n次,产生第n个差异。 |
| 19 | diff(X,n,dim) 它是沿标量暗指定的维度计算的第n个差异函数。 如果order n等于或超过维度dim的长度,则diff返回一个空数组。 |
| 20 | prod(A) 阵列元素的产品; 返回A的数组元素的乘积。
如果输入A是单个,则prod函数计算并返回B为单。 对于所有其他数字和逻辑数据类型,prod计算并将B返回为double。 |
| 21 | prod(A,dim) 返回维度dim的产品。 例如,如果A是矩阵,则prod(A,2)是包含每行的乘积的列向量。 |
| 22 | prod(___,datatype) 乘以并返回由datatype指定的类中的数组。 |
| 23 | sum(A)
|
| 24 | sum(A,dim) 沿着标量dim指定的A维的dim 。 |
| 25 | sum(..., 'double') sum(..., dim,'double') 以双精度执行添加并返回double类型的答案,即使A具有单数据类型或整数数据类型。 这是整数数据类型的默认值。 |
| 26 | sum(..., 'native') sum(..., dim,'native') 在A的本机数据类型中执行添加,并返回相同数据类型的答案。 这是single和double的默认值。 |
| 27 | ceil(A) 向正无穷大方向前进; 将A的元素舍入到最接近的大于或等于A的整数。 |
| 28 | fix(A) 向零回合 |
| 29 | floor(A) 向负无穷大方向转; 将A的元素舍入到最接近的小于或等于A的整数。 |
| 30 | idivide(a, b) idivide(a, b,'fix') 具有舍入选项的整数除法; 与a./b相同,除了小数商向零舍入到最接近的整数。 |
| 31 | idivide(a, b, 'round') 小数商舍入到最接近的整数。 |
| 32 | idivide(A, B, 'floor') 分数商向负无穷大舍入到最接近的整数。 |
| 33 | idivide(A, B, 'ceil') 分数商向无穷大舍入到最接近的整数。 |
| 34 | mod (X,Y) 分裂后的模数; 返回X - n。* Y其中n = floor(X./Y)。 如果Y不是整数且商X./Y在整数的舍入误差范围内,则n是该整数。 输入X和Y必须是相同大小的实数数组,或实数标量(提供Y~ = 0)。 请注意 -
|
| 35 | rem (X,Y) 分裂后剩余; 返回X - n。* Y其中n = fix(X./Y)。 如果Y不是整数且商X./Y在整数的舍入误差范围内,那么n就是整数。 输入X和Y必须是相同大小的实数数组,或实数标量(提供Y~ = 0)。 请注意 -
|
| 36 | round(X) 舍入到最接近的整数; 将X的元素舍入到最接近的整数。 小数部分为0.5的正元素向上舍入到最接近的正整数。 具有-0.5的小数部分的负元素向下舍入到最接近的负整数。 |