纸上谈兵: 左倾堆 (leftist heap)
我们之前讲解了堆(heap)的概念。堆是一个优先队列。每次从堆中取出的元素都是堆中优先级最高的元素。
在之前的文章中,我们基于完全二叉树(complete binary tree)实现了堆,这样的堆叫做二叉堆(binary heap)。binary heap有一个基本要求: 每个节点的优先级大于两个子节点的优先级。在这一要求下,堆的根节点始终是堆的元素中优先级最高的元素。此外,我们实现了delete_min()操作,从堆中取出元素;insert()操作,向堆中插入元素。
现在,我们考虑下面的问题: 如何合并(merge)两个堆呢? 一个方案是从第一个堆中不断取出一个元素,并插入到第二个堆中。这样,我们需要量级为n的操作。我们下面要实现更有效率的合并。
左倾堆 (Leftist Heap)
左倾堆基于二叉树(binary tree)。左倾堆的节点满足堆的基本要求,即(要求1)每个节点的优先级大于子节点的优先级。与二叉堆不同,左倾堆并不是完全二叉树。二叉堆是非常平衡的树结构,它的每一层都被填满(除了最下面一层)。左倾堆则是维持一种不平衡的结构: 它的左子树节点往往比右子树有更多的节点。

不平衡
左倾堆的每个节点有一个附加信息,即null path length (npl)。npl是从一个节点到一个最近的不满节点的路径长度(不满节点:两个子节点至少有一个为NULL)。一个叶节点的npl为0,一个NULL节点的npl为-1。
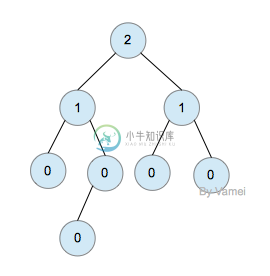
各个节点的npl (这里显示的不是元素值)
根据npl的定义,我们有推论1: 一个节点的npl等于子节点npl中最小值加1: npl(node) = min(npl(lchild), npl(rchild)) + 1
有了npl的概念,我们可以完整的定义左倾堆。左倾堆是一个符合下面要求的二叉树:
- 要求1: 每个节点的优先级大于子节点的优先级。
- 要求2: 对于任意节点的左右两个子节点,右子节点的npl不大于左子节点的npl。
左倾堆的性质
从上面的要求1和2可以知道,左倾堆的任意子树也是一个左倾堆。
由于左倾堆的特征,左倾堆的右侧路径(right path)较短。右侧路径是指我们从根节点开始,不断前往右子节点所构成的路径。对于一个左倾堆来说,右侧路径上节点数不大于任意其他路径上的节点数,否则,将违反左倾堆的要求2。
我们还可以证明推论2,如果一个左倾堆的右侧路径上有r个节点,那么该左倾堆将至少有2r-1个节点。我们采用归纳法证明:
- r = 1, 右侧路径上有一个节点,所以至少有21-1个节点
- 假设任意r, 左倾堆至少有2r-1节点。那么对于一个右侧路径节点数为r+1的左倾堆来说,根节点的右子树的右侧路径有r个节点。根节点的左子树的右侧路径至少有r个节点。根据假设,该左倾堆将包括:
- 右子树:至少有2r-1个节点
- 左子树: 至少有2r-1个节点
- 1个根节点
- 因此,对于r+1,整个左倾堆至少有2r+1-1个节点。证明完成
换句话说,一个n节点的的左倾堆,它的右侧路径最多有log(n+1)个节点。如果对右侧路径进行操作,其复杂度将是log(n)量级。
我们将沿着右侧路径进行左倾堆的合并操作。合并采用递归。合并如下:
- (base case) 如果一个空左倾堆与一个非空左倾堆合并,返回非空左倾堆
- 如果两个左倾堆都非空,那么比较两个根节点。取较小的根节点为新的根节点(满足要求1),合并较小根节点堆的右子堆与较大根节点堆。
- 如果右子堆npl > 左子堆npl,互换右子堆与左子堆。
- 更新根节点的npl = 右子堆npl + 1
上面的合并算法调用了合并操作自身,所以是递归。由于我们沿着右侧路径递归,所以复杂度是log(n)量级。
左倾堆的实现
上面可以看到,左倾堆可以相对高效的实现合并(merge)操作。
其他的堆操作,比如insert, delete_min都可以在merge基础上实现:
- 插入(insert): 将一个单节点左倾堆(新增节点)与一个已有左倾堆合并。
- 删除(delete_min): 删除根节点,将剩余的左右子堆合并。
/* By Vamei */
/*
* leftist heap
* bassed on binary tree
*/
#include <stdio.h>
#include <stdlib.h>
typedef struct node *position;
typedef int ElementTP;
struct node {
ElementTP element;
int npl;
position lchild;
position rchild;
};
typedef struct node *LHEAP;
LHEAP insert(ElementTP, LHEAP);
ElementTP find_min(LHEAP);
LHEAP delete_min(LHEAP);
LHEAP merge(LHEAP, LHEAP);
static LHEAP merge1(LHEAP, LHEAP);
static LHEAP swap_children(LHEAP);
int main(void)
{
LHEAP h1=NULL;
LHEAP h2=NULL;
h1 = insert(7, h1);
h1 = insert(3, h1);
h1 = insert(5, h1);
h2 = insert(2, h2);
h2 = insert(4, h2);
h2 = insert(8, h2);
h1 = merge(h1, h2);
printf("minimum: %d\n", find_min(h1));
return 0;
}
/*
* insert:
* merge a single-node leftist heap with a leftist heap
* */
LHEAP insert(ElementTP value, LHEAP h)
{
LHEAP single;
single = (position) malloc(sizeof(struct node));
// initialze
single->element = value;
single->lchild = NULL;
single->rchild = NULL;
return merge(single, h);
}
/*
* find_min:
* return root value in the tree
* */
ElementTP find_min(LHEAP h)
{
if(h != NULL) return h->element;
else exit(1);
}
/*
* delete_min:
* remove root, then merge two subheaps
* */
LHEAP delete_min(LHEAP h)
{
LHEAP l,r;
l = h->lchild;
r = h->rchild;
free(h);
return merge(l, r);
}
/*
* merge two leftist heaps
* */
LHEAP merge(LHEAP h1, LHEAP h2)
{
// if one heap is null, return the other
if(h1 == NULL) return h2;
if(h2 == NULL) return h1;
// if both are not null
if (h1->element < h2->element) {
return merge1(h1, h2);
}
else {
return merge1(h2, h1);
}
}
// h1->element < h2->element
static LHEAP merge1(LHEAP h1, LHEAP h2)
{
if (h1->lchild == NULL) {
/* h1 is a single node, npl is 0 */
h1->lchild = h2;
/* rchild is NULL, npl of h1 is still 0 */
}
else {
// left is not NULL
// merge h2 to right
// swap if necessary
h1->rchild = merge(h1->rchild, h2);
if(h1->lchild->npl < h1->rchild->npl) {
swap_children(h1);
}
h1->npl = h1->rchild->npl + 1; // update npl
}
return h1;
}
// swap: keep leftist property
static LHEAP swap_children(LHEAP h)
{
LHEAP tmp;
tmp = h->lchild;
h->lchild = h->rchild;
h->rchild = tmp;
}总结
左倾堆利用不平衡的节点分布,让右侧路径保持比较短的状态,从而提高合并的效率。
在合并过程,通过左右互换,来恢复左倾堆的性质。

