纸上谈兵: 数学归纳法, 递归, 栈

数学归纳法

数学归纳法(mathematical induction)是一种数学证明方法，常用于证明命题(命题是对某个现象的描述)在自然数范围内成立。随着现代数学的发展，自然数范围内的证明实际上构成了许多其他领域(比如数学分析)的基础，所以数学归纳法对于整个数学体系至关重要。

数学归纳法本身非常简单。如果我们想要证明某个命题对于自然数n都成立，那么:

第一步 证明命题对于n = 1成立。

第二步 假设命题对于n成立，n为任意自然数，证明在此假设下，命题对于n+1成立。

命题得证

想一下上面的两个步骤。它们实际上意味着，命题对于n = 1成立 -> 命题对于n = 2成立 -> 命题对于n = 3成立……直到无穷。因此，命题对于任意自然数都成立。这就好像多米诺骨牌，我们确定n的倒下会导致n + 1的倒下，然后推倒第一块骨牌，就能保证任意骨牌的倒下。

我们来看一下使用数学归纳法来证明高斯求和公式:

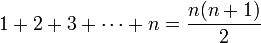
n为任意自然数。

(这个公式据说是高斯小学时想出来的。老师惩罚全班同学，必须算出1到100的累加，才能回家。于是高斯想出了上面的方法。天才都是被逼出来的么？)

我们的命题是: 高斯求和公式对于任意自然数n都成立。

下面为数学归纳法的证明步骤:

第一步 n = 1，等式左边(1的累加)为1，右边(右边公式代入n=1)也为1，等式两边相等，等式成立，因此命题对于 n = 1 成立。

第二步 假设上述公式对于任意n成立， 即1到n的累加为n*(n+1)/2

那么，对于n+1，等式的左边(从1到n+1的累加)等于n*(n+1)/2 + (n+1)，即(n+1)*(n+2)/2，

等式的右边的n用n+1代替，成为(n+1)*(n+2)/2，

等式两边相等，等式成立。因此，当假设命题对于n成立时，命题对于n+1成立。

因此，命题得证。

递归

递归(recursion)是计算机中的重要概念，它是指一个计算机程序调用其自身。为了保证计算机不陷入死循环，递归要求程序有一个能够达到的终止条件(base case)。比如下面的程序，是用于计算高斯求和公式:

/*
 * Gauss summation
 */

int f(n)
{
    if (n == 1) { 
        return 1;  // base case
    }
    else {
        return f(n-1) + n;  // induction
    }
}

在程序中规定了f(1)的值，以及f(n)和f(n-1)的关系。这正是数学归纳法思想的体现。想要得到f(n)，必须计算f(n-1)；想要f(n-1)，必须计算f(n-2)……直到f(1)。由于我们已经知道了f(1)的值，我们就可以填补前面所有的空缺，最终返回f(n)的值。

递归是数学归纳法在计算机中的程序实现。使用递归设计程序的时候，我们设置base case，并假设我们会获得n-1的结果，并实现n的结果。这就好像数学归纳法，我们只关注初始和衔接，而不需要关注具体的每一步。

栈

递归是用栈(stack)数据结构实现的。正如我们上面所说的，计算f(n)，需要f(n-1)；计算f(n-1)，需要f(n-2)……。我们在寻找到f(1)之前，会有许多空缺: f(n-1)的值什么？ f(n-2)的值是什么? …… f(2)的值是什么？f(1)的值是什么? 我们的第一个问题是f(n)是什么，结果，这个问题引出下一个问题，再下一个问题…… 每个问题的解答都依赖于下一个问题，直到我们找到第一个可以回答的问题: f(1)的值是什么?

我们用栈来保存我们在探索过程中的疑问。C语言中，函数的调用已经是用栈记录离场情境和返回地址。递归是函数对自身的调用，所以很自然的，递归用栈来保存我们的“疑问” 。

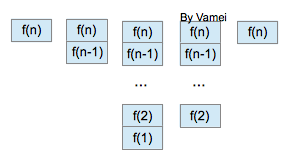
我们假设栈向下增长。首先，我们调用f(100)，那么当执行到

return f(n-1) + n; 

f(100)暂停执行，并记录当前的状态，比如n的值，当前执行到的位置。随后调用f(99)，栈增加一个frame，直到调用f(98) ... 栈不断增长，直到f(1)。f(1)得到结果1，并返回给f(2)。f(1)栈frame删除，转移到f(2)frame情境中继续执行

return f(n-1) + n; 

然后返回给f(3) ... 直到f(99)返回给f(100)，并执行

return f(n-1) + n; 

返回f(100)的值，得到结果。

上述过程是C编译器自动完成的。在实现递归算法时，也可以自行手动实现栈。这样可以得到更好的运行效率。

总结

数学归纳法

递归

栈