《摩尔线程》专题
-
二次贝塞尔曲线
贝塞尔曲线 Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线。 曲线定义:起始点、终止点、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。 1962年,法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法,并给出了详细的计算公式,因此按照这样的公式绘制出来的曲线就用他的姓氏来命名,称为贝塞尔曲线。 这里我们不介绍计算公式,只要知道贝塞尔曲线是一条由起始
-
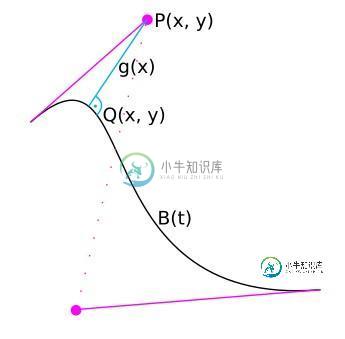 贝塞尔曲线到点的垂直线
贝塞尔曲线到点的垂直线我需要得到一条三次(2D)bezier曲线B(t)的点Q,其中从点Q到另一个给定点P的直线与bezier曲线垂直相交。 我知道:P,B(t) 我寻找:Q(基本上我想要g的斜率,但当我知道Q时,我可以很容易地计算出来,但g的斜率已经足够了) 注意,我认为这个ansatz是错误的。这只是为了完整性而包括的。 其中B(x)是笛卡尔坐标系下的bezier曲线,B'(x)是(笛卡尔坐标系下的)导数,k是与y
-
布尔值未在线程中更改
问题内容: 我有一个MPClient和MultiplayerMatch类。MultiplayerMatch在其构造函数中创建一个MPClient可运行线程。 为了避免数据溢出,我在MultiplayerMatch中有一个名为“ moved”的布尔值,当播放器移动时,它会变为true。 在updateMatch方法中,如果有任何播放器移动,则“ moved”变为true,这允许MPClient输入i
-
Spring靴子和祖尔路线
有一个简单的代理: 预过滤器: 和属性: 总的来说,一切正常。 但是代理发送的网页具有以下链接 必须采用如下形式: 如何配置服务器以发送正确的链接? 案例: 1.直接从Internet访问myserver时,例如: 服务器发送带有如下链接的页面: 2.从Internet访问代理时,如: 代理服务器发送带有以下链接的页面:
-
4.2.5 绘制贝塞尔曲线
贝塞尔曲线于1959年,由法国物理学家与数学家Paul de Casteljau所发明,于1962年,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,并用于汽车的车身设计。贝赛尔曲线为计算机矢量图形学奠定了基础,它的主要意义在于无论是直线或曲线都能在数学上予以描述。 贝塞尔曲线分为两种:二次贝塞尔曲线和三次贝塞尔曲线。 quadraticCurveTo()方法绘制二次贝塞尔曲线
-
1.4 绘制贝塞尔曲线
如果二次曲线不能满足你的需要,贝塞尔曲线可能会满足你。贝塞尔曲线又称三次曲线,是HTML5画布API所能支持的最高级的曲线。 图1-7 绘制贝塞尔曲线 绘制步骤 按照以下步骤绘制任意贝塞尔曲线: 1. 定义2D画布并设置曲线样式: window.onload = function(){ var canvas = document.getElementById("myCanvas");
-
刚体模拟摩擦
我目前正在做一个三维刚体模拟程序。我目前已经设法使刚体碰撞地板和弹跳正确地利用冲力。然而,我的问题是,一旦他们反弹,他们不断地加速,尽管使用摩擦矢量试图减缓他们。 谢谢 编辑:这里是集成代码。
-
javascript - 贝塞尔曲线运动帧?
这样的一个运动轨迹如何写,假设起点(295,0),终点(600,1000),运动时间2s, bang写一个动画帧keyframes, keyframes格式如下: https://cdn.alongweb.top/aa.mp4
-
使用摩卡设置 JSDOM
我正在尝试使用sinon的mock and spy来测试Redux组件和异步操作,但只要我将sinon导入任何测试文件,就会运行以下npm脚本: mocha -要求测试/助手/浏览器. js -编译器。:babel-core/register-opts test/client/* */*{js,jsx} -递归测试/客户端 我得到以下错误: 类型错误: document.createElement
-
如何在Java多线程中从线程2设置线程1的布尔标志
问题内容: 我写一个简单的应用程序,它涉及三个线程: ,和。 是 生成* 并馈给的生成器类。 * 消耗了 计算平均值。我的号码已经使用该饲料用。用途吃起来。 问题是:: 如果平均值超过中的1E5 ,我想表示停止产生数字。我有一个在需要被打开。我该如何实现? PS:该代码将永久运行,而无需在控制台上打印任何内容,我至今仍未弄清原因!! 问题答案: 您可以使用并将它传递给两个线程,原子类型是可访问的,
-
三维二次贝塞尔曲线(QuadraticBezierCurve3)
创建一条平滑的三维 二次贝塞尔曲线, 由起点、终点和一个控制点所定义。 代码示例 const curve = new THREE.QuadraticBezierCurve3( new THREE.Vector3( -10, 0, 0 ), new THREE.Vector3( 20, 15, 0 ), new THREE.Vector3( 10, 0, 0 ) ); const poi
-
二维二次贝塞尔曲线(QuadraticBezierCurve)
创建一条平滑的二维 二次贝塞尔曲线, 由起点、终点和一个控制点所定义。 代码示例 const curve = new THREE.QuadraticBezierCurve( new THREE.Vector2( -10, 0 ), new THREE.Vector2( 20, 15 ), new THREE.Vector2( 10, 0 ) ); const points = curv
-
三维三次贝塞尔曲线(CubicBezierCurve3)
创建一条平滑的三维 三次贝塞尔曲线, 由起点、终点和两个控制点所定义。 代码示例 const curve = new THREE.CubicBezierCurve3( new THREE.Vector3( -10, 0, 0 ), new THREE.Vector3( -5, 15, 0 ), new THREE.Vector3( 20, 15, 0 ), new THREE.Ve
-
二维三次贝塞尔曲线(CubicBezierCurve)
创建一条平滑的二维 三次贝塞尔曲线, 由起点、终点和两个控制点所定义。 代码示例 const curve = new THREE.CubicBezierCurve( new THREE.Vector2( -10, 0 ), new THREE.Vector2( -5, 15 ), new THREE.Vector2( 20, 15 ), new THREE.Vector2( 10,
-
在三次贝塞尔曲线上找到点的切线
问题内容: 对于三次贝塞尔曲线,通常具有四个点a,b,c和d, 对于给定的值t 如何最优雅地找到 切线 ? 问题答案: 这是经过完全测试的代码,可以复制和粘贴: 它沿着曲线绘制 近似 点, 并 绘制切线。 找到要点 找到切线 有 两个版本 的下面提供: 完美地工作。 完全相同,但以扩展,清晰,解释性的方式编写。它使算法更容易理解。 使用这两个例程之一:结果相同。 在这两种情况下,都可用于查找切线。
