空间（Spatial）

scipy.spatial package可以通过利用Qhull library来计算一组点的Triangulations，Voronoi Diagrams和Convex Qhull library 。 此外，它包含用于最近邻点查询的KDTree implementations以及用于各种度量中的距离计算的实用程序。

Delaunay三角测量

让我们了解Delaunay Triangulations是什么以及它们如何在SciPy中使用。

什么是Delaunay三角测量？

在数学和计算几何中，对于给定的平面中的离散点集合P的Delaunay三角剖分是三角测量DT(P) ，使得DT(P)中没有点在DT（P）中的任何三角形的外接圆内。

我们可以通过SciPy进行相同的计算。 让我们考虑以下示例。

from scipy.spatial import Delaunay
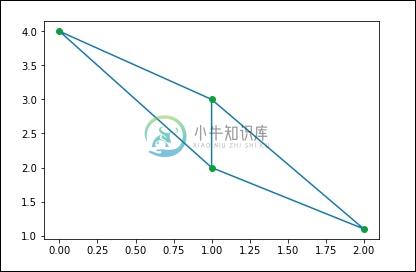
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()

上述程序将生成以下输出。

共面点数

让我们了解共面点是什么以及如何在SciPy中使用它们。

什么是共面点数？

共面点是位于同一平面内的三个或更多点。 回想一下，平面是一个平面，在所有方向上都没有尽头延伸。 它通常在数学教科书中显示为四面图。

让我们看看如何使用SciPy找到它。 让我们考虑以下示例。

from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanar

上述程序将生成以下输出。

array([[4, 0, 3]], dtype = int32)

这意味着点4位于三角形0和顶点3附近，但不包括在三角测量中。

凸壳

让我们了解凸壳是什么以及如何在SciPy中使用它们。

什么是Convex Hulls？

在数学中，欧几里得平面或欧几里德空间（或更一般地，在实数上的仿射空间中）的一组点X的convex hull或convex envelope是包含X的最小convex set 。

让我们考虑以下示例来详细了解它。

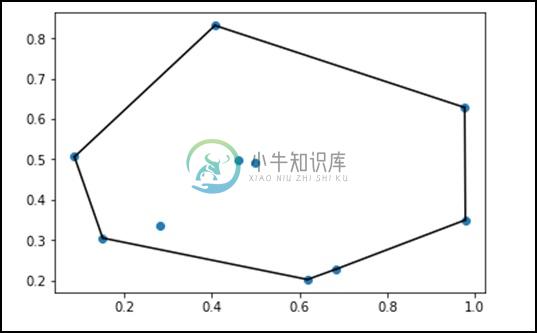
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()

上述程序将生成以下输出。