2.5. SciPy 中稀疏矩阵
2.5.1 介绍
(密集) 矩阵是:
- 数据对象
- 存储二维值数组的数据结构
重要特征:
- 一次分配所有项目的内存
- 通常是一个连续组块,想一想Numpy数组
- 快速访问个项目(*)
2.5.1.1 为什么有稀疏矩阵?
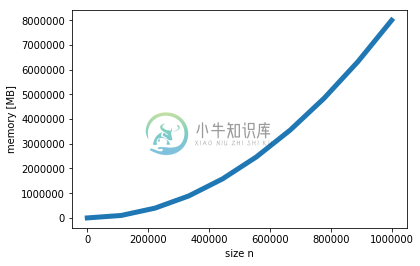
- 内存,增长是n**2
- 小例子(双精度矩阵):
In [2]:
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 1e6, 10)
plt.plot(x, 8.0 * (x**2) / 1e6, lw=5)
plt.xlabel('size n')
plt.ylabel('memory [MB]')
Out[2]:
<matplotlib.text.Text at 0x1122505c0>
2.5.1.2 稀疏矩阵 vs. 稀疏矩阵存储方案
- 稀疏矩阵是一个矩阵,绝大多数是空的
- 存储所有的0是浪费 -> 只存储非0项目
- 想一下压缩
- 有利: 巨大的内存节省
- 不利: 依赖实际的存储方案, (*) 通常并不能满足
2.5.1.3 典型应用
- 偏微分方程(PDES)的解
- 有限元素法
- 机械工程、电子、物理...
- 图论
- (i,j)不是0表示节点i与节点j是联接的
2.5.1.4 先决条件
最新版本的
numpyscipymatplotlib(可选)ipython(那些增强很方便)
2.5.1.5 稀疏结构可视化
- matplotlib中的
spy() - 样例绘图:
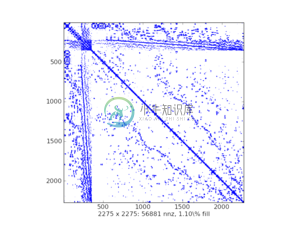

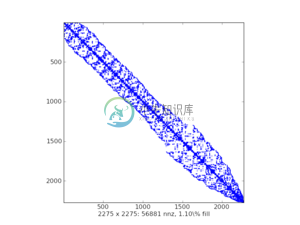
2.5.2 存储机制
- scipy.sparse中有七类稀疏矩阵:
- csc_matrix: 压缩列格式
- csr_matrix: 压缩行格式
- bsr_matrix: 块压缩行格式
- lil_matrix: 列表的列表格式
- dok_matrix: 值的字典格式
- coo_matrix: 座标格式 (即 IJV, 三维格式)
- dia_matrix: 对角线格式
- 每一个类型适用于一些任务
- 许多都利用了由Nathan Bell提供的稀疏工具 C++ 模块
- 假设导入了下列模块:
In [4]:
import numpy as np import scipy.sparse as sparse import matplotlib.pyplot as plt
- 给Numpy用户的warning:
- 使用'*'的乘是矩阵相乘 (点积)
- 并不是Numpy的一部分!
- 向Numpy函数传递一个稀疏矩阵希望一个ndarray/矩阵是没用的
2.5.2.1 通用方法
- 所有scipy.sparse类都是spmatrix的子类
- 算术操作的默认实现
- 通常转化为CSR
- 为了效率而子类覆盖
- 形状、数据类型设置/获取
- 非0索引
- 格式转化、与Numpy交互(toarray(), todense())
- ...
- 算术操作的默认实现
- 属性:
- mtx.A - 与mtx.toarray()相同
- mtx.T - 转置 (与mtx.transpose()相同)
- mtx.H - Hermitian (列举) 转置
- mtx.real - 复矩阵的真部
- mtx.imag - 复矩阵的虚部
- mtx.size - 非零数 (与self.getnnz()相同)
- mtx.shape - 行数和列数 (元组)
- 数据通常储存在Numpy数组中
2.5.2.2 稀疏矩阵类
2.5.2.2.1 对角线格式 (DIA)
- 非常简单的格式
- 形状 (n_diag, length) 的密集Numpy数组的对角线
- 固定长度 -> 当离主对角线比较远时会浪费空间
- _data_matrix的子类 (带数据属性的稀疏矩阵类)
- 每个对角线的偏移
- 0 是主对角线
- 负偏移 = 下面
- 正偏移 = 上面
- 快速矩阵 * 向量 (sparsetools)
- 快速方便的关于项目的操作
- 直接操作数据数组 (快速的NumPy机件)
- 构建器接受 :
- 密集矩阵 (数组)
- 稀疏矩阵
- 形状元组 (创建空矩阵)
- (数据, 偏移) 元组
- 没有切片、没有单个项目访问
- 用法 :
- 非常专业
- 通过有限微分解偏微分方程
- 有一个迭代求解器
2.5.2.2.1.1 示例
- 创建一些DIA矩阵 :
In [5]:
data = np.array([[1, 2, 3, 4]]).repeat(3, axis=0) data
Out[5]:
array([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])In [6]:
offsets = np.array([0, -1, 2]) mtx = sparse.dia_matrix((data, offsets), shape=(4, 4)) mtx
Out[6]:
<4x4 sparse matrix of type '<class 'numpy.int64'>' with 9 stored elements (3 diagonals) in DIAgonal format>
In [7]:
mtx.todense()
Out[7]:
matrix([[1, 0, 3, 0],
[1, 2, 0, 4],
[0, 2, 3, 0],
[0, 0, 3, 4]])In [8]:
data = np.arange(12).reshape((3, 4)) + 1 data
Out[8]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])In [9]:
mtx = sparse.dia_matrix((data, offsets), shape=(4, 4)) mtx.data
Out[9]:
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])In [10]:
mtx.offsets
Out[10]:
array([ 0, -1, 2], dtype=int32)
In [12]:
print(mtx)
(0, 0) 1 (1, 1) 2 (2, 2) 3 (3, 3) 4 (1, 0) 5 (2, 1) 6 (3, 2) 7 (0, 2) 11 (1, 3) 12
In [13]:
mtx.todense()
Out[13]:
matrix([[ 1, 0, 11, 0],
[ 5, 2, 0, 12],
[ 0, 6, 3, 0],
[ 0, 0, 7, 4]])- 机制的解释 :
偏移: 行
2: 9
1: --10------
0: 1 . 11 .
-1: 5 2 . 12
-2: . 6 3 .
-3: . . 7 4
---------8
- 矩阵-向量相乘
In [14]:
vec = np.ones((4, )) vec
Out[14]:
array([ 1., 1., 1., 1.])
In [15]:
mtx * vec
Out[15]:
array([ 12., 19., 9., 11.])
In [16]:
mtx.toarray() * vec
Out[16]:
array([[ 1., 0., 11., 0.],
[ 5., 2., 0., 12.],
[ 0., 6., 3., 0.],
[ 0., 0., 7., 4.]])2.5.2.2.2 列表的列表格式 (LIL)
- 基于行的联接列表
- 每一行是一个Python列表(排序的)非零元素的列索引
- 行存储在Numpy数组中 (dtype=np.object)
- 非零值也近似存储
- 高效增量构建稀疏矩阵
- 构建器接受 :
- 密集矩阵 (数组)
- 稀疏矩阵
- 形状元组 (创建一个空矩阵)
- 灵活切片、高效改变稀疏结构
- 由于是基于行的,算术和行切片慢
- 用途 :
- 当稀疏模式并不是已知的逻辑或改变
- 例子:从一个文本文件读取稀疏矩阵
2.5.2.2.2.1 示例
- 创建一个空的LIL矩阵 :
In [17]:
mtx = sparse.lil_matrix((4, 5))
- 准备随机数据:
In [18]:
from numpy.random import rand data = np.round(rand(2, 3)) data
Out[18]:
array([[ 1., 1., 1.],
[ 0., 1., 1.]])- 使用象征所以分配数据:
In [19]:
mtx[:2, [1, 2, 3]] = data mtx
Out[19]:
<4x5 sparse matrix of type '<class 'numpy.float64'>' with 5 stored elements in LInked List format>
In [21]:
print(mtx)
(0, 1) 1.0 (0, 2) 1.0 (0, 3) 1.0 (1, 2) 1.0 (1, 3) 1.0
In [22]:
mtx.todense()
Out[22]:
matrix([[ 0., 1., 1., 1., 0.],
[ 0., 0., 1., 1., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]])In [23]:
mtx.toarray()
Out[23]:
array([[ 0., 1., 1., 1., 0.],
[ 0., 0., 1., 1., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]])更多的切片和索引:
In [24]:
mtx = sparse.lil_matrix([[0, 1, 2, 0], [3, 0, 1, 0], [1, 0, 0, 1]]) mtx.todense()
Out[24]:
matrix([[0, 1, 2, 0],
[3, 0, 1, 0],
[1, 0, 0, 1]], dtype=int64)In [25]:
print(mtx)
(0, 1) 1 (0, 2) 2 (1, 0) 3 (1, 2) 1 (2, 0) 1 (2, 3) 1
In [26]:
mtx[:2, :]
Out[26]:
<2x4 sparse matrix of type '<class 'numpy.int64'>' with 4 stored elements in LInked List format>
In [27]:
mtx[:2, :].todense()
Out[27]:
matrix([[0, 1, 2, 0],
[3, 0, 1, 0]], dtype=int64)In [28]:
mtx[1:2, [0,2]].todense()
Out[28]:
matrix([[3, 1]], dtype=int64)
In [29]:
mtx.todense()
Out[29]:
matrix([[0, 1, 2, 0],
[3, 0, 1, 0],
[1, 0, 0, 1]], dtype=int64)2.5.2.2.3 值的字典格式 (DOK)
- Python字典的子类
- 键是 (行, 列) 索引元组 (不允许重复的条目)
- 值是对应的非零值
- 高效增量构建稀疏矩阵
- 构建器支持:
- 密集矩阵 (数组)
- 稀疏矩阵
- 形状元组 (创建空矩阵)
- 高效 O(1) 对单个元素的访问
- 灵活索引,改变稀疏结构是高效
- 一旦创建完成后可以被高效转换为coo_matrix
- 算术很慢 (循环用
dict.iteritems()) - 用法:
- 当稀疏模式是未知的假设或改变时
2.5.2.2.3.1 示例
- 逐个元素创建一个DOK矩阵:
In [30]:
mtx = sparse.dok_matrix((5, 5), dtype=np.float64) mtx
Out[30]:
<5x5 sparse matrix of type '<class 'numpy.float64'>' with 0 stored elements in Dictionary Of Keys format>
In [31]:
for ir in range(5):
for ic in range(5):
mtx[ir, ic] = 1.0 * (ir != ic)
mtx
Out[31]:
<5x5 sparse matrix of type '<class 'numpy.float64'>' with 20 stored elements in Dictionary Of Keys format>
In [32]:
mtx.todense()
Out[32]:
matrix([[ 0., 1., 1., 1., 1.],
[ 1., 0., 1., 1., 1.],
[ 1., 1., 0., 1., 1.],
[ 1., 1., 1., 0., 1.],
[ 1., 1., 1., 1., 0.]])- 切片与索引:
In [33]:
mtx[1, 1]
Out[33]:
0.0
In [34]:
mtx[1, 1:3]
Out[34]:
<1x2 sparse matrix of type '<class 'numpy.float64'>' with 1 stored elements in Dictionary Of Keys format>
In [35]:
mtx[1, 1:3].todense()
Out[35]:
matrix([[ 0., 1.]])
In [36]:
mtx[[2,1], 1:3].todense()
Out[36]:
matrix([[ 1., 0.],
[ 0., 1.]])2.5.2.2.4 座标格式 (COO)
- 也被称为 ‘ijv’ 或 ‘triplet’ 格式
- 三个NumPy数组: row, col, data
data[i]是在 (row[i], col[i]) 位置的值- 允许重复值
_data_matrix的子类 (带有data属性的稀疏矩阵类)- 构建稀疏矩阵的高速模式
- 构建器接受:
- 密集矩阵 (数组)
- 稀疏矩阵
- 形状元组 (创建空数组)
(data, ij)元组
- 与CSR/CSC格式非常快的互相转换
- 快速的矩阵 * 向量 (sparsetools)
- 快速而简便的逐项操作
- 直接操作数据数组 (快速NumPy机制)
- 没有切片,没有算术 (直接)
- 使用:
- 在各种稀疏格式间的灵活转换
- 当转化到其他形式 (通常是 CSR 或 CSC), 重复的条目被加总到一起
- 有限元素矩阵的快速高效创建
2.5.2.2.4.1 示例
- 创建空的COO矩阵:
In [37]:
mtx = sparse.coo_matrix((3, 4), dtype=np.int8) mtx.todense()
Out[37]:
matrix([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=int8)- 用 (data, ij) 元组创建:
In [38]:
row = np.array([0, 3, 1, 0]) col = np.array([0, 3, 1, 2]) data = np.array([4, 5, 7, 9]) mtx = sparse.coo_matrix((data, (row, col)), shape=(4, 4)) mtx
Out[38]:
<4x4 sparse matrix of type '<class 'numpy.int64'>' with 4 stored elements in COOrdinate format>
In [39]:
mtx.todense()
Out[39]:
matrix([[4, 0, 9, 0],
[0, 7, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 5]])2.5.2.2.5 压缩稀疏行格式 (CSR)
- 面向行
- 三个Numpy数组:
indices,indptr,dataindices是列索引的数组data是对应的非零值数组indptr指向行开始的所以和数据- 长度是
n_row + 1, 最后一个项目 = 值数量 =indices和data的长度 - i-th行的非零值是列索引为
indices[indptr[i]:indptr[i+1]]的data[indptr[i]:indptr[i+1]] - 项目 (i, j) 可以通过
data[indptr[i]+k], k是j在indices[indptr[i]:indptr[i+1]]的位置来访问
_cs_matrix(常规 CSR/CSC 功能) 的子类_data_matrix(带有data属性的稀疏矩阵类) 的子类
- 三个Numpy数组:
- 快速矩阵向量相乘和其他算术 (sparsetools)
- 构建器接受:
- 密集矩阵 (数组)
- 稀疏矩阵
- 形状元组 (创建空矩阵)
(data, ij)元组(data, indices, indptr)元组
- 高效行切片,面向行的操作
- 较慢的列切片,改变稀疏结构代价昂贵
- 用途:
- 实际计算 (大多数线性求解器都支持这个格式)
2.5.2.2.5.1 示例
- 创建空的CSR矩阵:
In [40]:
mtx = sparse.csr_matrix((3, 4), dtype=np.int8) mtx.todense()
Out[40]:
matrix([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=int8)- 用
(data, ij)元组创建:
In [41]:
row = np.array([0, 0, 1, 2, 2, 2]) col = np.array([0, 2, 2, 0, 1, 2]) data = np.array([1, 2, 3, 4, 5, 6]) mtx = sparse.csr_matrix((data, (row, col)), shape=(3, 3)) mtx
Out[41]:
<3x3 sparse matrix of type '<class 'numpy.int64'>' with 6 stored elements in Compressed Sparse Row format>
In [42]:
mtx.todense()
Out[42]:
matrix([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]], dtype=int64)In [43]:
mtx.data
Out[43]:
array([1, 2, 3, 4, 5, 6], dtype=int64)
In [44]:
mtx.indices
Out[44]:
array([0, 2, 2, 0, 1, 2], dtype=int32)
In [45]:
mtx.indptr
Out[45]:
array([0, 2, 3, 6], dtype=int32)
用(data, indices, indptr)元组创建:
In [46]:
data = np.array([1, 2, 3, 4, 5, 6]) indices = np.array([0, 2, 2, 0, 1, 2]) indptr = np.array([0, 2, 3, 6]) mtx = sparse.csr_matrix((data, indices, indptr), shape=(3, 3)) mtx.todense()
Out[46]:
matrix([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]])2.5.2.2.6 压缩稀疏列格式 (CSC)
- 面向列
- 三个Numpy数组:
indices、indptr、data indices是行索引的数组data是对应的非零值indptr指向indices和data开始的列- 长度是
n_col + 1, 最后一个条目 = 值数量 =indices和data的长度 - 第i列的非零值是行索引为
indices[indptr[i]:indptr[i+1]]的data[indptr[i]:indptr[i+1]] - 项目 (i, j) 可以作为
data[indptr[j]+k]访问, k是i在indices[indptr[j]:indptr[j+1]]的位置 _cs_matrix的子类 (通用的 CSR/CSC 功能性)_data_matrix的子类 (带有data属性的稀疏矩阵类)
- 三个Numpy数组:
- 快速的矩阵和向量相乘及其他数学 (sparsetools)
- 构建器接受:
- 密集矩阵 (数组)
- 稀疏矩阵
- 形状元组 (创建空矩阵)
(data, ij)元组(data, indices, indptr)元组
- 高效列切片、面向列的操作
- 较慢的行切片、改变稀疏结构代价昂贵
- 用途:
- 实际计算 (巨大多数线性求解器支持这个格式)
2.5.2.2.6.1 示例
- 创建空CSC矩阵:
In [47]:
mtx = sparse.csc_matrix((3, 4), dtype=np.int8) mtx.todense()
Out[47]:
matrix([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=int8)- 用
(data, ij)元组创建:
In [48]:
row = np.array([0, 0, 1, 2, 2, 2]) col = np.array([0, 2, 2, 0, 1, 2]) data = np.array([1, 2, 3, 4, 5, 6]) mtx = sparse.csc_matrix((data, (row, col)), shape=(3, 3)) mtx
Out[48]:
<3x3 sparse matrix of type '<class 'numpy.int64'>' with 6 stored elements in Compressed Sparse Column format>
In [49]:
mtx.todense()
Out[49]:
matrix([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]], dtype=int64)In [50]:
mtx.data
Out[50]:
array([1, 4, 5, 2, 3, 6], dtype=int64)
In [51]:
mtx.indices
Out[51]:
array([0, 2, 2, 0, 1, 2], dtype=int32)
In [52]:
mtx.indptr
Out[52]:
array([0, 2, 3, 6], dtype=int32)
- 用
(data, indices, indptr)元组创建:
In [53]:
data = np.array([1, 4, 5, 2, 3, 6]) indices = np.array([0, 2, 2, 0, 1, 2]) indptr = np.array([0, 2, 3, 6]) mtx = sparse.csc_matrix((data, indices, indptr), shape=(3, 3)) mtx.todense()
Out[53]:
matrix([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]])2.5.2.2.7 块压缩行格式 (BSR)
- 本质上,CSR带有密集的固定形状的子矩阵而不是纯量的项目
- 块大小
(R, C)必须可以整除矩阵的形状(M, N) - 三个Numpy数组:
indices、indptr、dataindices是每个块列索引的数组data是形状为(nnz, R, C)对应的非零值- ...
_cs_matrix的子类 (通用的CSR/CSC功能性)_data_matrix的子类 (带有data属性的稀疏矩阵类)
- 块大小
- 快速矩阵向量相乘和其他的算术 (sparsetools)
- 构建器接受:
- 密集矩阵 (数组)
- 稀疏矩阵
- 形状元组 (创建空的矩阵)
(data, ij)元组(data, indices, indptr)元组
- 许多对于带有密集子矩阵的稀疏矩阵算术操作比CSR更高效很多
- 用途:
- 类似CSR
- 有限元素向量值离散化
##### 2.5.2.2.7.1 示例
- 创建空的
(1, 1)块大小的(类似CSR...)的BSR矩阵:
In [54]:
mtx = sparse.bsr_matrix((3, 4), dtype=np.int8) mtx
Out[54]:
<3x4 sparse matrix of type '<class 'numpy.int8'>' with 0 stored elements (blocksize = 1x1) in Block Sparse Row format>
In [55]:
mtx.todense()
Out[55]:
matrix([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=int8)- 创建块大小
(3, 2)的空BSR矩阵:
In [59]:
mtx = sparse.bsr_matrix((3, 4), blocksize=(3, 2), dtype=np.int8) mtx
Out[59]:
<3x4 sparse matrix of type '<class 'numpy.int8'>' with 0 stored elements (blocksize = 3x2) in Block Sparse Row format>
- 一个bug?
- 用
(1, 1)块大小 (类似 CSR...)(data, ij)的元组创建:
In [60]:
row = np.array([0, 0, 1, 2, 2, 2]) col = np.array([0, 2, 2, 0, 1, 2]) data = np.array([1, 2, 3, 4, 5, 6]) mtx = sparse.bsr_matrix((data, (row, col)), shape=(3, 3)) mtx
Out[60]:
<3x3 sparse matrix of type '<class 'numpy.int64'>' with 6 stored elements (blocksize = 1x1) in Block Sparse Row format>
In [61]:
mtx.todense()
Out[61]:
matrix([[1, 0, 2],
[0, 0, 3],
[4, 5, 6]], dtype=int64)In [62]:
mtx.indices
Out[62]:
array([0, 2, 2, 0, 1, 2], dtype=int32)
In [63]:
mtx.indptr
Out[63]:
array([0, 2, 3, 6], dtype=int32)
- 用
(2, 1)块大小(data, indices, indptr)的元组创建:
In [64]:
indptr = np.array([0, 2, 3, 6]) indices = np.array([0, 2, 2, 0, 1, 2]) data = np.array([1, 2, 3, 4, 5, 6]).repeat(4).reshape(6, 2, 2) mtx = sparse.bsr_matrix((data, indices, indptr), shape=(6, 6)) mtx.todense()
Out[64]:
matrix([[1, 1, 0, 0, 2, 2],
[1, 1, 0, 0, 2, 2],
[0, 0, 0, 0, 3, 3],
[0, 0, 0, 0, 3, 3],
[4, 4, 5, 5, 6, 6],
[4, 4, 5, 5, 6, 6]])In [65]:
data
Out[65]:
array([[[1, 1],
[1, 1]],
[[2, 2],
[2, 2]],
[[3, 3],
[3, 3]],
[[4, 4],
[4, 4]],
[[5, 5],
[5, 5]],
[[6, 6],
[6, 6]]])2.5.2.3 总结
存储机制的总结
| 格式 | 矩阵 * 向量 | 提取项目 | 灵活提取 | 设置项目 | 灵活设置 | 求解器 | 备注 |
|---|---|---|---|---|---|---|---|
| DIA | sparsetools | . | . | . | . | 迭代 | 有数据数组,专门化 |
| LIL | 通过 CSR | 是 | 是 | 是 | 是 | 迭代 | 通过CSR的算术, 增量构建 |
| DOK | python | 是 | 只有一个轴 | 是 | 是 | 迭代 | O(1)条目访问, 增量构建 |
| COO | sparsetools | . | . | . | . | 迭代 | 有数据数组, 便利的快速转换 |
| CSR | sparsetools | 是 | 是 | 慢 | . | 任何 | 有数据数组, 快速以行为主的操作 |
| CSC | sparsetools | 是 | 是 | 慢 | . | 任何 | 有数据数组, 快速以列为主的操作 |
| BSR | sparsetools | . | . | . | . | 专门化 | 有数据数组,专门化 |

