C++稀疏矩阵的各种基本运算并实现加法乘法

代码：

#include <iostream>
#include<malloc.h>
#include<cstdio>
using namespace std;
#define M 4
#define N 4
#define MaxSize 100
typedef int ElemType;
typedef struct
{
  int r;
  int c;
  ElemType d;///元素值
} TupNode; ///三元组定义
typedef struct
{
  int rows;
  int cols;
  int nums;
  TupNode data[MaxSize];
} TSMatrix; ///三元组顺序表定义
void CreatMat(TSMatrix &t,ElemType A[M][N])
{
  t.rows=M;
  t.cols=N;
  t.nums=0;
  for(int i=0; i<M; i++)
    for(int j=0; j<N; j++)
      if(A[i][j]!=0)
      {
        t.data[t.nums].r=i;
        t.data[t.nums].c=j;
        t.data[t.nums].d=A[i][j];
        t.nums++;
      }
}
bool Value(TSMatrix &t,ElemType x,int i,int j)
{
  int k=0,k1;
  if(i>=t.rows||j>=t.cols)
    return false;
  while(k<t.nums&&i>t.data[k].r)k++;
  while(k<t.nums&&i==t.data[k].r&&j>t.data[k].c)k++;
  if(t.data[k].r==i&&t.data[k].c==j)
    t.data[k].d=x;
  else
  {
    for(k1=t.nums-1; k1>=k; k1--)
    {
      t.data[k1+1].r=t.data[k].r;
      t.data[k1+1].c=t.data[k].c;
      t.data[k1+1].d=t.data[k].d;
    }
    t.data[k].r=i;
    t.data[k].c=j;
    t.data[k].d=x;
    t.nums++;
  }
  return true;
}
bool Assign(TSMatrix t,ElemType &x,int i,int j)
{
  int k=0;
  if(i>=t.rows||j>=t.cols)
    return false;
  while(k<t.nums&&i>t.data[k].r)k++;
  while(k<t.nums&&i==t.data[k].r&&j>t.data[k].c)k++;
  if(t.data[k].r==i&&t.data[k].c==j)
    x=t.data[k].d;
  else
    x=0;
  return true;
}
void DispMat(TSMatrix t)
{
  if(t.nums<=0)
    return ;
  printf("\t%d\t%d\t%d\n",t.rows,t.cols,t.nums);
  printf("\t-----------------\n");
  for(int i=0; i<t.nums; i++)
    printf("\t%d\t%d\t%d\n",t.data[i].r,t.data[i].c,t.data[i].d);
}
void TranMat(TSMatrix t,TSMatrix &tb)
{
  int i,j,k=0;
  tb.rows=t.cols;
  tb.cols=t.rows;
  tb.nums=t.nums;
  if(t.nums!=0)
  {
    for(i=0; i<t.cols; i++)
      for(j=0; j<t.nums; j++)
        if(t.data[j].c==i)
        {
          tb.data[k].r=t.data[j].c;
          tb.data[k].c=t.data[j].r;
          tb.data[k].d=t.data[j].d;
          k++;
        }
  }
}
bool MatAdd(TSMatrix a,TSMatrix b,TSMatrix &c)
{
  int i=0,j=0,k=0;
  ElemType v;
  if(a.rows!=b.rows||a.cols!=b.cols)
    return false;
  c.rows=a.rows;
  c.cols=a.cols;
  while(i<a.nums&&j<b.nums)
  {
    if(a.data[i].r==b.data[j].r)///先控制行相等
    {
      if(a.data[i].c<b.data[j].c)
      {
        c.data[k].r=a.data[i].r;
        c.data[k].c=a.data[i].c;
        c.data[k].d=a.data[i].d;
        k++;
        i++;
      }
      else if(a.data[i].c>b.data[j].c)
      {
        c.data[k].r=b.data[j].r;
        c.data[k].c=b.data[j].c;
        c.data[k].d=b.data[j].d;
        k++;
        j++;
      }
      else
      {
        v=a.data[i].d+b.data[j].d;
        if(v!=0)
        {
          c.data[k].r=a.data[i].r;
          c.data[k].c=a.data[i].c;
          c.data[k].d=v;
          k++;
        }
        i++;
        j++;
      }
    }
    else if(a.data[i].r<b.data[j].r)
    {
      c.data[k].r=a.data[i].r;
      c.data[k].c=a.data[i].c;
      c.data[k].d=a.data[i].d;
      k++;
      i++;
    }
    else
    {
      c.data[k].r=b.data[j].r;
      c.data[k].c=b.data[j].c;
      c.data[k].d=b.data[j].d;
      k++;
      j++;
    }
    c.nums=k;
  }
  return true;
}
int getvalue(TSMatrix c,int i,int j)
{
  int k=0;
  while(k<c.nums&&(c.data[k].r!=i||c.data[k].c!=j))
    k++;
  if(k<c.nums)
    return (c.data[k].d);
  else
    return (0);
}
bool MatMul(TSMatrix a,TSMatrix b,TSMatrix &c)
{
  int i,j,k,p=0;
  ElemType s;
  if(a.cols!=b.rows)
    return false;
  for(i=0; i<a.rows; i++)
    for(j=0; j<b.cols; j++)
    {
      s=0;
      for(k=0; k<a.cols; k++)
        s+=getvalue(a,i,k)*getvalue(b,k,j);
      if(s!=0)
      {
        c.data[p].r=i;
        c.data[p].c=j;
        c.data[p].d=s;
        p++;
      }
    }
  c.rows=a.rows;
  c.cols=b.cols;
  c.nums=p;
  return true;
}
int main()
{
  ElemType a1[N][N]={{1,0,3,0},{0,1,0,0},{0,0,1,0},{0,0,1,1}};
  ElemType b1[M][M]={{3,0,0,0},{0,4,0,0},{0,0,1,0},{0,0,0,2}};
  TSMatrix a,b,c;
  CreatMat(a,a1);
  CreatMat(b,b1);
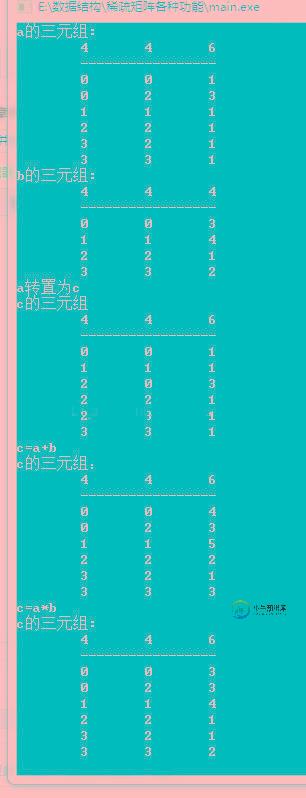
  printf("a的三元组:\n");
  DispMat(a);
  printf("b的三元组:\n");
  DispMat(b);
  printf("a转置为c\n");
  TranMat(a,c);
  printf("c的三元组\n");
  DispMat(c);
  printf("c=a+b\n");
  MatAdd(a,b,c);
  printf("c的三元组：\n");
  DispMat(c);
  printf("c=a*b\n");
  MatMul(a,b,c);
  printf("c的三元组:\n");
  DispMat(c);
  return 0;
}

总结

以上就是这篇文章的全部内容了，希望本文的内容对大家的学习或者工作具有一定的参考学习价值，谢谢大家对小牛知识库的支持。如果你想了解更多相关内容请查看下面相关链接