7.5 Verilog FFT 设计

精华

小牛编辑

220浏览

2023-03-14

FFT（Fast Fourier Transform），快速傅立叶变换，是一种 DFT（离散傅里叶变换）的高效算法。在以时频变换分析为基础的数字处理方法中，有着不可替代的作用。

FFT 原理

公式推导

DFT 的运算公式为：

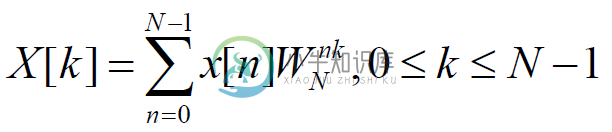
其中，

将离散傅里叶变换公式拆分成奇偶项，则前 N/2 个点可以表示为：

同理，后 N/2 个点可以表示为：

由此可知，后 N/2 个点的值完全可以通过计算前 N/2 个点时的中间过程值确定。对 A[k] 与 B[k] 继续进行奇偶分解，直至变成 2 点的 DFT，这样就可以避免很多的重复计算，实现了快速离散傅里叶变换（FFT）的过程。

算法结构

8 点 FFT 计算的结构示意图如下。

由图可知，只需要简单的计算几次乘法和加法，便可完成离散傅里叶变换过程，而不是对每个数据进行繁琐的相乘和累加。

重要特性

(1) 级的概念

每分割一次，称为一级运算。

设 FFT 运算点数为 N，共有 M 级运算，则它们满足：

每一级运算的标识为 m = 0, 1, 2, ..., M-1。

为了便于分割计算，FFT 点数 N 的取值经常为 2 的整数次幂。

(2) 蝶形单元

FFT 计算结构由若干个蝶形运算单元组成，每个运算单元示意图如下：

蝶形单元的输入输出满足：

其中，

每一个蝶形单元运算时，进行了一次乘法和两次加法。

每一级中，均有 N/2 个蝶形单元。

故完成一次 FFT 所需要的乘法次数和加法次数分别为：

(3) 组的概念

每一级 N/2 个蝶形单元可分为若干组，每一组有着相同的结构与因子分布。

例如 m=0 时，可以分为 N/2=4 组。

m=1 时，可以分为 N/4=2 组。

m=M-1 时，此时只能分为 1 组。

(4) 因子分布因子存在于 m 级，其中。

在 8 点 FFT 第二级运算中，即 m=1 ，蝶形运算因子可以化简为：

(5) 码位倒置

对于 N=8 点的 FFT 计算，X(0) ~ X(7) 位置对应的 2 进制码为：

X(000), X(001), X(010), X(011), X(100), X(101), X(110), X(111)

将其位置的 2 进制码进行翻转：

X(000), X(100), X(010), X(110), X(001), X(101), X(011), X(111)

此时位置对应的 10 进制为：

X(0), X(4), X(2), X(6), X(1), X(5), X(3), X(7)

恰好对应 FFT 第一级输入数据的顺序。

该特性有利于 FFT 的编程实现。

FFT 设计

设计说明

为了利用仿真简单的说明 FFT 的变换过程，数据点数取较小的值 8。

如果数据是串行输入，需要先进行缓存，所以设计时数据输入方式为并行。

数据输入分为实部和虚部共 2 部分，所以计算结果也分为实部和虚部。

设计采用流水结构，暂不考虑资源消耗的问题。

为了使设计结构更加简单，这里做一步妥协，乘法计算直接使用乘号。如果 FFT 设计应用于实际，一定要将乘法结构换成可以流水的乘法器，或使用官方提供的效率较高的乘法器 IP。

蝶形单元设计

蝶形单元为定点运算，需要对旋转因子进行定点量化。

借助 matlab 将旋转因子扩大 8192 倍（左移 13 位），可参考附录。

为了防止蝶形运算中的乘法和加法导致位宽逐级增大，每一级运算完成后，要对输出数据进行固定位宽的截位，也可去掉旋转因子倍数增大而带来的影响。代码如下：

实例

`timescale 1ns / 100ps
/**************** butter unit *************************
Xm(p) ------------------------> Xm+1(p)
- ->
- -
-
- -
- ->
Xm(q) ------------------------> Xm+1(q)
Wn -1
*/ /////////////////////////////////////////////////////
module butterfly
(
input clk ,
input rstn ,
input en ,
input signed [ 23 : 0 ] xp_real , // Xm(p)
input signed [ 23 : 0 ] xp_imag ,
input signed [ 23 : 0 ] xq_real , // Xm(q)
input signed [ 23 : 0 ] xq_imag ,
input signed [ 15 : 0 ] factor_real , // Wnr
input signed [ 15 : 0 ] factor_imag ,

output valid ,
output signed [ 23 : 0 ] yp_real , //Xm+1(p)
output signed [ 23 : 0 ] yp_imag ,
output signed [ 23 : 0 ] yq_real , //Xm+1(q)
output signed [ 23 : 0 ] yq_imag ) ;

reg [ 4 : 0 ] en_r ;
always @ ( posedge clk or negedge rstn ) begin
if ( !rstn ) begin
en_r <= 'b0 ;
end
else begin
en_r <= {en_r [ 3 : 0 ] , en } ;
end
end

//=====================================================//
//(1.0) Xm(q) mutiply and Xm(p) delay
reg signed [ 39 : 0 ] xq_wnr_real0 ;
reg signed [ 39 : 0 ] xq_wnr_real1 ;
reg signed [ 39 : 0 ] xq_wnr_imag0 ;
reg signed [ 39 : 0 ] xq_wnr_imag1 ;
reg signed [ 39 : 0 ] xp_real_d ;
reg signed [ 39 : 0 ] xp_imag_d ;
always @ ( posedge clk or negedge rstn ) begin
if ( !rstn ) begin
xp_real_d <= 'b0 ;
xp_imag_d <= 'b0 ;
xq_wnr_real0 <= 'b0 ;
xq_wnr_real1 <= 'b0 ;
xq_wnr_imag0 <= 'b0 ;
xq_wnr_imag1 <= 'b0 ;
end
else if (en ) begin
xq_wnr_real0 <= xq_real * factor_real ;
xq_wnr_real1 <= xq_imag * factor_imag ;
xq_wnr_imag0 <= xq_real * factor_imag ;
xq_wnr_imag1 <= xq_imag * factor_real ;
//expanding 8192 times as Wnr
xp_real_d <= { { 4 {xp_real [ 23 ] } } , xp_real [ 22 : 0 ] , 1 3'b0 } ;
xp_imag_d <= { { 4 {xp_imag [ 23 ] } } , xp_imag [ 22 : 0 ] , 1 3'b0 } ;
end
end

//(1.1) get Xm(q) mutiplied-results and Xm(p) delay again
reg signed [ 39 : 0 ] xp_real_d1 ;
reg signed [ 39 : 0 ] xp_imag_d1 ;
reg signed [ 39 : 0 ] xq_wnr_real ;
reg signed [ 39 : 0 ] xq_wnr_imag ;
always @ ( posedge clk or negedge rstn ) begin
if ( !rstn ) begin
xp_real_d1 <= 'b0 ;
xp_imag_d1 <= 'b0 ;
xq_wnr_real <= 'b0 ;
xq_wnr_imag <= 'b0 ;
end
else if (en_r [ 0 ] ) begin
xp_real_d1 <= xp_real_d ;
xp_imag_d1 <= xp_imag_d ;
//提前设置好位宽余量，防止数据溢出
xq_wnr_real <= xq_wnr_real0 - xq_wnr_real1 ;
xq_wnr_imag <= xq_wnr_imag0 + xq_wnr_imag1 ;
end
end

//======================================================//
//(2.0) butter results
reg signed [ 39 : 0 ] yp_real_r ;
reg signed [ 39 : 0 ] yp_imag_r ;
reg signed [ 39 : 0 ] yq_real_r ;
reg signed [ 39 : 0 ] yq_imag_r ;
always @ ( posedge clk or negedge rstn ) begin
if ( !rstn ) begin
yp_real_r <= 'b0 ;
yp_imag_r <= 'b0 ;
yq_real_r <= 'b0 ;
yq_imag_r <= 'b0 ;
end
else if (en_r [ 1 ] ) begin
yp_real_r <= xp_real_d1 + xq_wnr_real ;
yp_imag_r <= xp_imag_d1 + xq_wnr_imag ;
yq_real_r <= xp_real_d1 - xq_wnr_real ;
yq_imag_r <= xp_imag_d1 - xq_wnr_imag ;
end
end

//(3) discard the low 13bits because of Wnr
assign yp_real = {yp_real_r [ 39 ] , yp_real_r [ 13 + 23 : 13 ] } ;
assign yp_imag = {yp_imag_r [ 39 ] , yp_imag_r [ 13 + 23 : 13 ] } ;
assign yq_real = {yq_real_r [ 39 ] , yq_real_r [ 13 + 23 : 13 ] } ;
assign yq_imag = {yq_imag_r [ 39 ] , yq_imag_r [ 13 + 23 : 13 ] } ;
assign valid = en_r [ 2 ] ;

endmodule

顶层例化

根据 FFT 算法结构示意图，将蝶形单元例化，完成最后的 FFT 功能。

可根据每一级蝶形单元的输入输出对应关系，依次手动例化 12 次，也可利用 generate 进行例化，此时就需要非常熟悉 FFT 中"组"和"级"的特点：

(1) 8 点 FFT 设计，需要 3 级运算，每一级有 4 个蝶形单元，每一级的组数目分别是 4、2、1。
(2) 每一级的组内一个蝶形单元中两个输入端口的距离恒为（m 为级标号，对应左移运算 1<<m），组内两个蝶形单元的第一个输入端口间的距离为 1。
(3) 每一级相邻组间的第一个蝶形单元的第一个输入端口的距离为（对应左移运算 2<<m）。

例化代码如下。

其中，矩阵信号 xm_real（xm_imag）的一维、二维地址是代表级和组的标识。

在判断信号端口之间的连接关系时，使用了看似复杂的判断逻辑，而且还带有乘号，其实最终生成的电路和手动编写代码例化 12 个蝶形单元的方式是完全相同的。因为 generate 中的变量只是辅助生成实际的电路，相关值的计算判断都已经在编译时完成。这些变量更不会生成实际的电路，只是为更快速的模块例化提供了一种方法。

实例

timescale 1ns / 100ps
module fft8 (
input clk ,
input rstn ,
input en ,

input signed [ 23 : 0 ] x0_real ,
input signed [ 23 : 0 ] x0_imag ,
input signed [ 23 : 0 ] x1_real ,
input signed [ 23 : 0 ] x1_imag ,
input signed [ 23 : 0 ] x2_real ,
input signed [ 23 : 0 ] x2_imag ,
input signed [ 23 : 0 ] x3_real ,
input signed [ 23 : 0 ] x3_imag ,
input signed [ 23 : 0 ] x4_real ,
input signed [ 23 : 0 ] x4_imag ,
input signed [ 23 : 0 ] x5_real ,
input signed [ 23 : 0 ] x5_imag ,
input signed [ 23 : 0 ] x6_real ,
input signed [ 23 : 0 ] x6_imag ,
input signed [ 23 : 0 ] x7_real ,
input signed [ 23 : 0 ] x7_imag ,

output valid ,
output signed [ 23 : 0 ] y0_real ,
output signed [ 23 : 0 ] y0_imag ,
output signed [ 23 : 0 ] y1_real ,
output signed [ 23 : 0 ] y1_imag ,
output signed [ 23 : 0 ] y2_real ,
output signed [ 23 : 0 ] y2_imag ,
output signed [ 23 : 0 ] y3_real ,
output signed [ 23 : 0 ] y3_imag ,
output signed [ 23 : 0 ] y4_real ,
output signed [ 23 : 0 ] y4_imag ,
output signed [ 23 : 0 ] y5_real ,
output signed [ 23 : 0 ] y5_imag ,
output signed [ 23 : 0 ] y6_real ,
output signed [ 23 : 0 ] y6_imag ,
output signed [ 23 : 0 ] y7_real ,
output signed [ 23 : 0 ] y7_imag
) ;

//operating data
wire signed [ 23 : 0 ] xm_real [ 3 : 0 ] [ 7 : 0 ] ;
wire signed [ 23 : 0 ] xm_imag [ 3 : 0 ] [ 7 : 0 ] ;
wire en_connect [ 15 : 0 ] ;
assign en_connect [ 0 ] = en ;
assign en_connect [ 1 ] = en ;
assign en_connect [ 2 ] = en ;
assign en_connect [ 3 ] = en ;

//factor, multiplied by 0x2000
wire signed [ 15 : 0 ] factor_real [ 3 : 0 ] ;
wire signed [ 15 : 0 ] factor_imag [ 3 : 0 ] ;
assign factor_real [ 0 ] = 1 6'h2000 ; //1
assign factor_imag [ 0 ] = 1 6'h0000 ; //0
assign factor_real [ 1 ] = 1 6'h16a0 ; //sqrt(2)/2
assign factor_imag [ 1 ] = 1 6'he95f ; //-sqrt(2)/2
assign factor_real [ 2 ] = 1 6'h0000 ; //0
assign factor_imag [ 2 ] = 1 6'he000 ; //-1
assign factor_real [ 3 ] = 1 6'he95f ; //-sqrt(2)/2
assign factor_imag [ 3 ] = 1 6'he95f ; //-sqrt(2)/2

//输入初始化，和码位有关倒置
assign xm_real [ 0 ] [ 0 ] = x0_real ;
assign xm_real [ 0 ] [ 1 ] = x4_real ;
assign xm_real [ 0 ] [ 2 ] = x2_real ;
assign xm_real [ 0 ] [ 3 ] = x6_real ;
assign xm_real [ 0 ] [ 4 ] = x1_real ;
assign xm_real [ 0 ] [ 5 ] = x5_real ;
assign xm_real [ 0 ] [ 6 ] = x3_real ;
assign xm_real [ 0 ] [ 7 ] = x7_real ;
assign xm_imag [ 0 ] [ 0 ] = x0_imag ;
assign xm_imag [ 0 ] [ 1 ] = x4_imag ;
assign xm_imag [ 0 ] [ 2 ] = x2_imag ;
assign xm_imag [ 0 ] [ 3 ] = x6_imag ;
assign xm_imag [ 0 ] [ 4 ] = x1_imag ;
assign xm_imag [ 0 ] [ 5 ] = x5_imag ;
assign xm_imag [ 0 ] [ 6 ] = x3_imag ;
assign xm_imag [ 0 ] [ 7 ] = x7_imag ;

//butter instantiaiton
//integer index[11:0] ;
genvar m , k ;
generate
//3 stage
for (m = 0 ; m <= 2 ; m =m + 1 ) begin : stage
for (k = 0 ; k <= 3 ; k =k + 1 ) begin : unit

butterfly u_butter (
.clk (clk ) ,
.rstn (rstn ) ,
.en (en_connect [m * 4 + k ] ) ,
//是否再组内？组编号+组内编号：下组编号+新组内编号
.xp_real (xm_real [ m ] [k [m : 0 ] < ( 1 <<m ) ?
(k [ 3 :m ] << (m + 1 ) ) + k [m : 0 ] :
(k [ 3 :m ] << (m + 1 ) ) + (k [m : 0 ] - ( 1 <<m ) ) ] ) ,
.xp_imag (xm_imag [ m ] [k [m : 0 ] < ( 1 <<m ) ?
(k [ 3 :m ] << (m + 1 ) ) + k [m : 0 ] :
(k [ 3 :m ] << (m + 1 ) ) + (k [m : 0 ] - ( 1 <<m ) ) ] ) ,
.xq_real (xm_real [ m ] [ (k [m : 0 ] < ( 1 <<m ) ?
(k [ 3 :m ] << (m + 1 ) ) + k [m : 0 ] :
(k [ 3 :m ] << (m + 1 ) ) + (k [m : 0 ] - ( 1 <<m ) ) ) + ( 1 <<m ) ] ) , //增加蝶形单元两个输入端口间距离
.xq_imag (xm_imag [ m ] [ (k [m : 0 ] < ( 1 <<m ) ?
(k [ 3 :m ] << (m + 1 ) ) + k [m : 0 ] :
(k [ 3 :m ] << (m + 1 ) ) + (k [m : 0 ] - ( 1 <<m ) ) ) + ( 1 <<m ) ] ) ,

.factor_real (factor_real [k [m : 0 ] < ( 1 <<m ) ?
k [m : 0 ] : k [m : 0 ] - ( 1 <<m ) ] ) ,
.factor_imag (factor_imag [k [m : 0 ] < ( 1 <<m ) ?
k [m : 0 ] : k [m : 0 ] - ( 1 <<m ) ] ) ,

//output data
.valid (en_connect [ (m + 1 ) * 4 + k ] ) ,
.yp_real (xm_real [ m + 1 ] [k [m : 0 ] < ( 1 <<m ) ?
(k [ 3 :m ] << (m + 1 ) ) + k [m : 0 ] :
(k [ 3 :m ] << (m + 1 ) ) + (k [m : 0 ] - ( 1 <<m ) ) ] ) ,
.yp_imag (xm_imag [ m + 1 ] [ (k [m : 0 ] ) < ( 1 <<m ) ?
(k [ 3 :m ] << (m + 1 ) ) + k [m : 0 ] :
(k [ 3 :m ] << (m + 1 ) ) + (k [m : 0 ] - ( 1 <<m ) ) ] ) ,
.yq_real (xm_real [ m + 1 ] [ (k [m : 0 ] < ( 1 <<m ) ?
(k [ 3 :m ] << (m + 1 ) ) + k [m : 0 ] :
(k [ 3 :m ] << (m + 1 ) ) + (k [m : 0 ] - ( 1 <<m ) ) ) + ( 1 <<m ) ] ) ,
.yq_imag (xm_imag [ m + 1 ] [ ( (k [m : 0 ] ) < ( 1 <<m ) ?
(k [ 3 :m ] << (m + 1 ) ) + k [m : 0 ] :
(k [ 3 :m ] << (m + 1 ) ) + (k [m : 0 ] - ( 1 <<m ) ) ) + ( 1 <<m ) ] )
) ;
end
end
endgenerate

assign valid = en_connect [ 12 ] ;
assign y0_real = xm_real [ 3 ] [ 0 ] ;
assign y0_imag = xm_imag [ 3 ] [ 0 ] ;
assign y1_real = xm_real [ 3 ] [ 1 ] ;
assign y1_imag = xm_imag [ 3 ] [ 1 ] ;
assign y2_real = xm_real [ 3 ] [ 2 ] ;
assign y2_imag = xm_imag [ 3 ] [ 2 ] ;
assign y3_real = xm_real [ 3 ] [ 3 ] ;
assign y3_imag = xm_imag [ 3 ] [ 3 ] ;
assign y4_real = xm_real [ 3 ] [ 4 ] ;
assign y4_imag = xm_imag [ 3 ] [ 4 ] ;
assign y5_real = xm_real [ 3 ] [ 5 ] ;
assign y5_imag = xm_imag [ 3 ] [ 5 ] ;
assign y6_real = xm_real [ 3 ] [ 6 ] ;
assign y6_imag = xm_imag [ 3 ] [ 6 ] ;
assign y7_real = xm_real [ 3 ] [ 7 ] ;
assign y7_imag = xm_imag [ 3 ] [ 7 ] ;

endmodule

testbench

testbench 编写如下，主要用于 16 路实、复数据的连续输入。因为每次 FFT 只有 8 点数据，所以送入的数据比较随意，并不是正弦波等规则的数据。

实例

`timescale 1ns / 100ps
module test ;
reg clk ;
reg rstn ;
reg en ;

reg signed [ 23 : 0 ] x0_real ;
reg signed [ 23 : 0 ] x0_imag ;
reg signed [ 23 : 0 ] x1_real ;
reg signed [ 23 : 0 ] x1_imag ;
reg signed [ 23 : 0 ] x2_real ;
reg signed [ 23 : 0 ] x2_imag ;
reg signed [ 23 : 0 ] x3_real ;
reg signed [ 23 : 0 ] x3_imag ;
reg signed [ 23 : 0 ] x4_real ;
reg signed [ 23 : 0 ] x4_imag ;
reg signed [ 23 : 0 ] x5_real ;
reg signed [ 23 : 0 ] x5_imag ;
reg signed [ 23 : 0 ] x6_real ;
reg signed [ 23 : 0 ] x6_imag ;
reg signed [ 23 : 0 ] x7_real ;
reg signed [ 23 : 0 ] x7_imag ;

wire valid ;
wire signed [ 23 : 0 ] y0_real ;
wire signed [ 23 : 0 ] y0_imag ;
wire signed [ 23 : 0 ] y1_real ;
wire signed [ 23 : 0 ] y1_imag ;
wire signed [ 23 : 0 ] y2_real ;
wire signed [ 23 : 0 ] y2_imag ;
wire signed [ 23 : 0 ] y3_real ;
wire signed [ 23 : 0 ] y3_imag ;
wire signed [ 23 : 0 ] y4_real ;
wire signed [ 23 : 0 ] y4_imag ;
wire signed [ 23 : 0 ] y5_real ;
wire signed [ 23 : 0 ] y5_imag ;
wire signed [ 23 : 0 ] y6_real ;
wire signed [ 23 : 0 ] y6_imag ;
wire signed [ 23 : 0 ] y7_real ;
wire signed [ 23 : 0 ] y7_imag ;

initial begin
clk = 0 ; //50MHz
rstn = 0 ;
# 10 rstn = 1 ;
forever begin
# 10 clk = ~clk ; //50MHz
end
end

fft8 u_fft (
.clk (clk ) ,
.rstn (rstn ) ,
.en (en ) ,
.x0_real (x0_real ) ,
.x0_imag (x0_imag ) ,
.x1_real (x1_real ) ,
.x1_imag (x1_imag ) ,
.x2_real (x2_real ) ,
.x2_imag (x2_imag ) ,
.x3_real (x3_real ) ,
.x3_imag (x3_imag ) ,
.x4_real (x4_real ) ,
.x4_imag (x4_imag ) ,
.x5_real (x5_real ) ,
.x5_imag (x5_imag ) ,
.x6_real (x6_real ) ,
.x6_imag (x6_imag ) ,
.x7_real (x7_real ) ,
.x7_imag (x7_imag ) ,

.valid (valid ) ,
.y0_real (y0_real ) ,
.y0_imag (y0_imag ) ,
.y1_real (y1_real ) ,
.y1_imag (y1_imag ) ,
.y2_real (y2_real ) ,
.y2_imag (y2_imag ) ,
.y3_real (y3_real ) ,
.y3_imag (y3_imag ) ,
.y4_real (y4_real ) ,
.y4_imag (y4_imag ) ,
.y5_real (y5_real ) ,
.y5_imag (y5_imag ) ,
.y6_real (y6_real ) ,
.y6_imag (y6_imag ) ,
.y7_real (y7_real ) ,
.y7_imag (y7_imag ) ) ;

//data input
initial begin
en = 0 ;
x0_real = 2 4'd10 ;
x1_real = 2 4'd20 ;
x2_real = 2 4'd30 ;
x3_real = 2 4'd40 ;
x4_real = 2 4'd10 ;
x5_real = 2 4'd20 ;
x6_real = 2 4'd30 ;
x7_real = 2 4'd40 ;

x0_imag = 2 4'd0 ;
x1_imag = 2 4'd0 ;
x2_imag = 2 4'd0 ;
x3_imag = 2 4'd0 ;
x4_imag = 2 4'd0 ;
x5_imag = 2 4'd0 ;
x6_imag = 2 4'd0 ;
x7_imag = 2 4'd0 ;
@ ( negedge clk ) ;
en = 1 ;
forever begin
@ ( negedge clk ) ;
x0_real = (x0_real > 2 2'h3F_ffff ) ? 'b0 : x0_real + 1 ;
x1_real = (x1_real > 2 2'h3F_ffff ) ? 'b0 : x1_real + 1 ;
x2_real = (x2_real > 2 2'h3F_ffff ) ? 'b0 : x2_real + 31 ;
x3_real = (x3_real > 2 2'h3F_ffff ) ? 'b0 : x3_real + 1 ;
x4_real = (x4_real > 2 2'h3F_ffff ) ? 'b0 : x4_real + 23 ;
x5_real = (x5_real > 2 2'h3F_ffff ) ? 'b0 : x5_real + 1 ;
x6_real = (x6_real > 2 2'h3F_ffff ) ? 'b0 : x6_real + 6 ;
x7_real = (x7_real > 2 2'h3F_ffff ) ? 'b0 : x7_real + 1 ;

x0_imag = (x0_imag > 2 2'h3F_ffff ) ? 'b0 : x0_imag + 2 ;
x1_imag = (x1_imag > 2 2'h3F_ffff ) ? 'b0 : x1_imag + 5 ;
x2_imag = (x2_imag > 2 2'h3F_ffff ) ? 'b0 : x2_imag + 3 ;
x3_imag = (x3_imag > 2 2'h3F_ffff ) ? 'b0 : x3_imag + 6 ;
x4_imag = (x4_imag > 2 2'h3F_ffff ) ? 'b0 : x4_imag + 4 ;
x5_imag = (x5_imag > 2 2'h3F_ffff ) ? 'b0 : x5_imag + 8 ;
x6_imag = (x6_imag > 2 2'h3F_ffff ) ? 'b0 : x6_imag + 11 ;
x7_imag = (x7_imag > 2 2'h3F_ffff ) ? 'b0 : x7_imag + 7 ;
end
end

//finish simulation
initial # 1000 $finish ;
endmodule

仿真结果

大致可以看出，FFT 结果可以流水输出。

用 matlab 自带的 FFT 函数对相同数据进行运算，前 2 组数据 FFT 结果如下。

可以看出，第一次输入的数据信号只有实部有效时，FFT 结果是完全一样的。

但是第二次输入的数据复部也有信号，此时两者之间的结果开始有误差，有时误差还很大。

用 matlab 对 Verilog 实现的 FFT 过程进行模拟，发现此过程的 FFT 结果和 Verilog 实现的 FFT 结果基本一致。

将有误差的两种 FFT 结果取绝对值进行比较，图示如下。

可以看出，FFT 结果的趋势大致相同，但在个别点有肉眼可见的误差。

设计总结：

就如设计蝶形单元时所说，旋转因子量化时，位宽的选择就会引入误差。

而且每个蝶形单元的运算结果都会进行截取，也会引入误差。

matlab 计算 FFT 时不用考虑精度问题，以其最高精度对数据进行 FFT 计算。

以上所述，都会导致最后两种 FFT 计算方式结果的差异。

感兴趣的学者，可以将旋转因子和输入数据位宽再进行一定的增加，FFT 点数也可以增加，然后再进行仿真对比，相对误差应该会减小。

附录：matlab 使用

生成旋转因子

8 点 FFT 只需要用到 4 个旋转因子。旋转因子扩大倍数为 8192。

实例

clear all ;close all ;clc ;
%=======================================================
% Wnr calcuting
%=======================================================
for r = 0 : 3
Wnr_factor = cos (pi / 4 *r ) - j *sin (pi / 4 *r ) ;
Wnr_integer = floor (Wnr_factor * 2 ^ 13 ) ;

if ( real (Wnr_integer ) < 0 )
Wnr_real = real (Wnr_integer ) + 2 ^ 16 ; %负数的补码
else
Wnr_real = real (Wnr_integer ) ;
end
if (imag (Wnr_integer ) < 0 )
Wnr_imag = imag (Wnr_integer ) + 2 ^ 16 ;
else
Wnr_imag = imag (Wnr_integer ) ;
end

Wnr ( 2 *r + 1 ,: ) = dec2hex (Wnr_real ) %实部
Wnr ( 2 *r + 2 ,: ) = dec2hex (Wnr_imag ) %虚部
end

FFT 结果对比

matlab 模拟 Verilog 实现 FFT 的过程如下，也包括 2 种 FFT 结果的对比。

实例

clear all ;close all ;clc ;
%=======================================================
% 8dots fft
%=======================================================
for r = 0 : 3
Wnr (r + 1 ) = cos (pi / 4 *r ) - j *sin (pi / 4 *r ) ;
end
x = [ 10 , 20 , 30 , 40 , 10 , 20 , 30 , 40 ] ;
step = [ 1 +2j , 1 +5j , 31 +3j , 1 +6j , 23 +4j , 1 +8j , 6 +11j , 1 +7j ] ;
x2 = x + step ;
xm0 = [x2 ( 0 + 1 ) , x2 ( 4 + 1 ) , x2 ( 2 + 1 ) , x2 ( 6 + 1 ) , x2 ( 1 + 1 ) , x2 ( 5 + 1 ) , x2 ( 3 + 1 ) , x2 ( 7 + 1 ) ] ;

%% stage1
xm1 ( 1 ) = xm0 ( 1 ) + xm0 ( 2 ) *Wnr ( 1 ) ;
xm1 ( 2 ) = xm0 ( 1 ) - xm0 ( 2 ) *Wnr ( 1 ) ;
xm1 ( 3 ) = xm0 ( 3 ) + xm0 ( 4 ) *Wnr ( 1 ) ;
xm1 ( 4 ) = xm0 ( 3 ) - xm0 ( 4 ) *Wnr ( 1 ) ;
xm1 ( 5 ) = xm0 ( 5 ) + xm0 ( 6 ) *Wnr ( 1 ) ;
xm1 ( 6 ) = xm0 ( 5 ) - xm0 ( 6 ) *Wnr ( 1 ) ;
xm1 ( 7 ) = xm0 ( 7 ) + xm0 ( 8 ) *Wnr ( 1 ) ;
xm1 ( 8 ) = xm0 ( 7 ) - xm0 ( 8 ) *Wnr ( 1 ) ;
floor (xm1 ( : ) )

%% stage2
xm2 ( 1 ) = xm1 ( 1 ) + xm1 ( 3 ) *Wnr ( 1 ) ;
xm2 ( 3 ) = xm1 ( 1 ) - xm1 ( 3 ) *Wnr ( 1 ) ;
xm2 ( 2 ) = xm1 ( 2 ) + xm1 ( 4 ) *Wnr ( 2 ) ;
xm2 ( 4 ) = xm1 ( 2 ) - xm1 ( 4 ) *Wnr ( 2 ) ;
xm2 ( 5 ) = xm1 ( 5 ) + xm1 ( 7 ) *Wnr ( 1 ) ;
xm2 ( 7 ) = xm1 ( 5 ) - xm1 ( 7 ) *Wnr ( 1 ) ;
xm2 ( 6 ) = xm1 ( 6 ) + xm1 ( 8 ) *Wnr ( 2 ) ;
xm2 ( 8 ) = xm1 ( 6 ) - xm1 ( 8 ) *Wnr ( 2 ) ;
floor (xm2 ( : ) )

%% stage3
xm3 ( 1 ) = xm2 ( 1 ) + xm2 ( 5 ) *Wnr ( 1 ) ;
xm3 ( 5 ) = xm2 ( 1 ) - xm2 ( 5 ) *Wnr ( 1 ) ;
xm3 ( 2 ) = xm2 ( 2 ) + xm2 ( 6 ) *Wnr ( 2 ) ;
xm3 ( 6 ) = xm2 ( 2 ) - xm2 ( 6 ) *Wnr ( 2 ) ;
xm3 ( 3 ) = xm2 ( 3 ) + xm2 ( 7 ) *Wnr ( 3 ) ;
xm3 ( 7 ) = xm2 ( 3 ) - xm2 ( 7 ) *Wnr ( 3 ) ;
xm3 ( 4 ) = xm2 ( 4 ) + xm2 ( 8 ) *Wnr ( 4 ) ;
xm3 ( 8 ) = xm2 ( 4 ) - xm2 ( 8 ) *Wnr ( 4 ) ;
floor (xm3 ( : ) )

%% fft
fft1 = fft (x )
fft2 = fft (x2 )
plot ( 1 : 8 , abs (fft2 ) )
hold on
plot ( 1 : 8 , abs (xm3 ) , 'r' )

源码下载

Download