TensorFlow数学基础

在TensorFlow中创建基本应用程序之前，了解TensorFlow所需的数学概念非常重要。数学是任何机器学习算法的核心。在数学核心概念的帮助下，定义了特定机器学习算法的解决方案。

向量

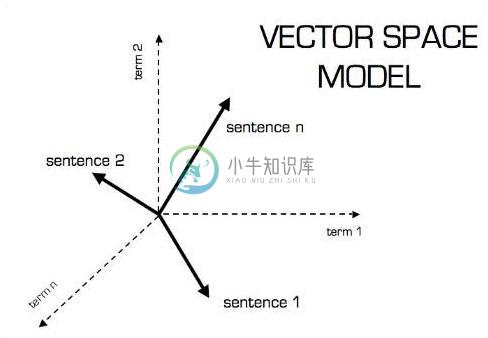
将数字数组(连续或离散)定义为向量。机器学习算法处理固定长度向量以产生更好的输出。

机器学习算法处理多维数据，因此向量起着至关重要的作用。

矢量模型的图形表示如下所示 -

标量

标量可以定义为一维向量。标量是那些仅包括大小而没有方向的标量。对于标量，我们只关注幅度。

标量的示例：儿童的体重和身高参数。

矩阵

矩阵可以定义为多维数组，以行和列的格式排列。矩阵的大小由行长度和列长度定义。下图显示了任何指定矩阵的表示。

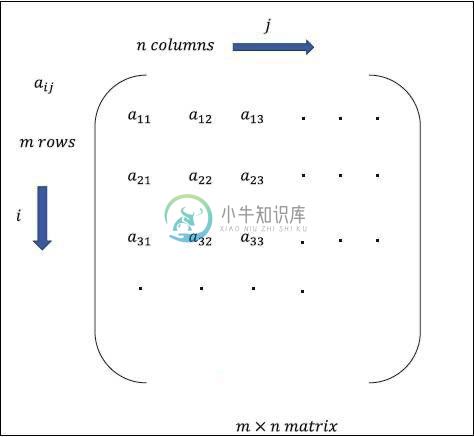
考虑如上所述的具有“m”行和“n”列的矩阵，矩阵表示将指定为“m * n矩阵”，其也定义了矩阵的长度。

数学计算

在本节中，我们将了解TensorFlow中的数学计算。

矩阵相加
如果矩阵具有相同的尺寸，则可以相加两个或更多个矩阵。相加表示根据给定位置添加每个元素。

请考虑以下示例以了解矩阵的相加方式是如何工作的 -

矩阵减法
矩阵的减法以类似于添加两个矩阵的方式操作。如果尺寸相等，用户可以减去两个矩阵。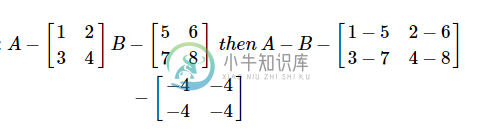

矩阵乘法
对于两个矩阵A m * n和B p * q是可乘的，n应该等于p。得到的矩阵是 -

矩阵的转置
矩阵A，m * n的转置通常由AT(转置)n * m表示，并且通过将列向量转置为行向量而获得。

矢量的点积
尺寸n的任何矢量可以表示为矩阵v = R ^ n * 1。

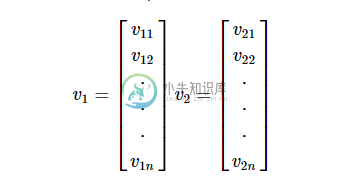
两个向量的点积是相应组件的乘积之和 - 沿相同维度的组件，可以表示为：

矢量点积的例子如下 -