《红黑树》专题
-
在二叉搜索树中查找数据点的深度
这是家庭作业。不要只发布代码。 我需要在二进制搜索树中找到给定数据点的深度。我实现了一个<code>depth()</code>方法和一个helper方法<code>countNodes()</code>,它递归地对节点进行计数。 如果我们要搜索的数据不在树中,我需要返回< code>-1。根据我的递归,我看不出这怎么可能。
-
删除二进制搜索树
我试着删除二叉查找树的节点,当我打印出来的时候,我得到的结果实际上不是这个删除,实际上可以删除二叉树本身的任何键。 我是二进制搜索树的新手。有人能帮我写代码吗?我们将感谢您的帮助。 谢谢 完整代码
-
打印有深度的二叉查找树
我需要打印一个具有深度和从高到低的二叉搜索树,根据深度,在打印节点之前增加破折号的数量。树根用0破折号,她的树梢用1破折号……我可以打印没有破折号的树,但我不知道如何用破折号打印。我用的是C.对不起我的英语不好
-
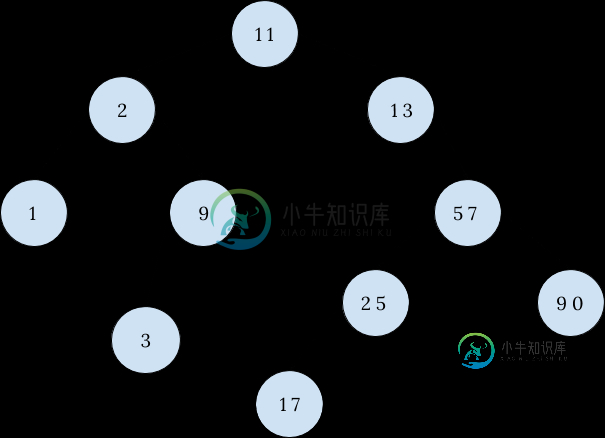 使用 C 查找搜索二叉树中的最长路径
使用 C 查找搜索二叉树中的最长路径我很难找到使用递归函数查找搜索二叉树的最长路径的代码。 bst_node是搜索二叉树的节点。 退出递归的条件非常简单: 在进行递归之前,打印节点的值: 如果假设深度x处的节点只有一个左子节点,那么最长路径穿过节点的左子节点,通过使用递归,我们可以这样写: 如果深度x处的节点只有右子节点,则最长路径穿过节点的右子节点,通过使用递归,我们可以像这样编写它 但是,如果节点同时具有左子项和右子项怎么办?我
-
树视图项中的绑定错误(水平和垂直内容对齐)
我得到这些错误。我读了几个帖子,我的TreeViewItem确实定义了Horizontal和VerticalContentAlignment。有趣的是。NET 4.0让这个错误消失了(我使用3.5 -否则我会遭受这个https://connect . Microsoft . com/visual studio/feedback/details/588343/changed-behavior-fro
-
修改二进制搜索树
我正在尝试为二叉搜索树类编写一种方法来修改平衡的普通树,这使得树仅在一侧具有节点。 从元素在不平衡树中出现的顺序来看,依序遍历(左、中、右)之间似乎存在某种关系。
-
二进制搜索树-实现“搜索”功能
我正在尝试实现一个二叉查找树,但是“搜索”函数对于除了根之外的每个条目都返回了错误的值。 该函数应返回其值与键参数匹配的节点的地址,如果节点不存在,则返回 NULL。 当我运行代码时,我得到以下内容: 我知道每个节点的“左”和“右”指针链接正确,因为“delAll”函数成功删除了所有节点。 将“cout”语句添加到“search”函数表明该函数似乎返回了正确的地址。为什么从主主调用时会打印错误的地
-
查找二叉查找树中小于给定值的所有值的算法
让一个整数的二进制搜索树创建一个包含所有小于给定整数x值的整数的链表。 我试过什么? 1)粗暴的解决方案(效率低下) BST 的顺序访问,我在列表中为每个整数 int the BST 插入一个节点,然后我从 x 开始释放列表中的每个节点 2)效率更高但错误 我进行了一次搜索,当我找到x时,我创建了一个列表,其中有序地访问了我找到x的节点的左边的子节点。 这显然是错误的,例如考虑到以下BST: 对于
-
二叉树:最小值和最大值之间所有节点的总和
我有一个任务,给我一个随机生成的BST的根。我得到了随机生成的测试用例。 分配说明如下: 您将得到二叉搜索树的根节点T和两个整数:min和max。确定存储在T中大于或等于min且小于或等于max的所有键的总和。递归地实现算法 我不允许使用全局变量或创建辅助函数 我当前的代码是: 我的问题是,如果在递归过程中的任何时候,节点都会触发基本情况,并导致我的函数无法正确完成。我相信我的命令可能是罪魁祸首。
-
二进制搜索树节点大小
我对如何在二叉查找树中排列节点的顺序有点困惑。左边的二叉查找树中的子树节点能比根节点大吗? 例如,以下内容会是二叉搜索树吗? 上面让我困惑的是1(3)的右子树是否可以大于原始根节点(2)。
-
考试:删除二叉搜索树的节点
当删除具有两个子节点的节点时,如果指示使用标准的二叉搜索树节点删除算法,我们应该将其替换为右子树的最小节点还是左子树的最大节点?
-
从二叉搜索树中删除元素
我在做作业,实现自己的二叉查找树。问题是,我们有自己的节点实现,它的父节点是不可直接访问的。 我一直在寻找答案,但我不想完全照搬解决方案,尽管如此,我似乎仍然没有得到正确的答案。我错过了一些元素没有被删除的情况。 你能帮帮我吗?我做错了什么? 这是删除方法: 节点使用通用接口 只有比较的方法。它看起来像这样 我在remove中使用了另一种方法,它设置节点的父节点的子节点,具体取决于它的左子节点还是
-
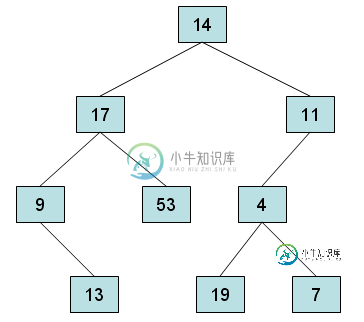 二进制搜索树节点删除未删除替换Java
二进制搜索树节点删除未删除替换Java我正在尝试从二叉查找树中删除节点。我可以成功地删除树上的任何其他节点,除了一个特殊的情况。如果目标节点有两个子节点,左边的子节点有右边的子树,我可以定位正确的替换节点,并将值切换到目标节点,但替换节点永远不会被删除。 看看上面的图片,如果我尝试删除17,程序将正确地导航到13,并用13替换17,但它不会像预期的那样删除原来的13。 我附加了我的remove方法和其中引用的方法。 这是我的Node类
-
使用递归删除二进制搜索树
从二叉查找树中删除节点时,您可以将节点替换为左侧的最大子节点或右侧的最小子节点。 我很难理解以下实现执行删除操作的方式。 上面的代码包括以下步骤: < li >查找替换节点。 < li >让替换节点引用已删除节点的左右子节点。 < li >让已删除节点的左右子节点将替换节点作为父节点。 < li >让替换节点引用已删除节点的父节点作为自己的父节点。 < li >清理。 我有困难的部分特别是递归。据
-
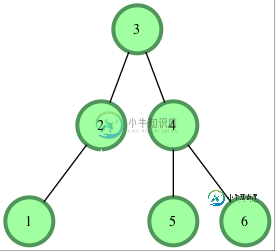 二叉树验证
二叉树验证一直在研究一些黑客等级破解编码面试问题,最近才发现这一个:二叉树问题。 在问题描述中,作者介绍了被认为是有效的二叉树的内容。 “节点左侧子树中每个节点的值都小于该节点的数据值。 然而他们提到这棵树 是有效的。但根据他们对有效二叉搜索树的描述,这棵树不是无效的吗,因为节点4有一个节点5的左子节点,后者更大。还是我误解了什么是有效的BST?
