《红黑树》专题
-
“ MVN依赖项：树”-是否有等效项可用于“详细”输出？
问题内容： 我有一个用例，我们希望了解每个Maven项目从每个依赖树获取的所有版本，即使它们被省略。 每个 maven-dependency-plugin 文档中，“ verbose”选项已停止使用，因为依赖目标的Maven 3和“ tree” Mojo不能更有效地显示省略的依赖。 我正在使用Maven 3.5.0，并尝试使用Maven 2.x的其他安装，但是这会产生与Java 8应用程序的兼容性
-
Java树数据结构？
问题内容： 是否有一个良好的可用（标准Java）数据结构来表示Java中的树？ 具体来说，我需要代表以下内容： 任何节点上的树都可以有任意数量的子代 每个节点（在根之后）只是一个字符串（其子代也是字符串） 我需要能够获得代表给定节点的输入字符串的所有子代（某种形式的列表或字符串数组） 是否有可用的结构或者我需要创建自己的结构（如果这样的话，实施建议会很好）。 问题答案： 这里： 那是可用于或任
-
bs4。FeatureNotFound:找不到具有您请求的功能的树生成器：lxml。您需要安装解析器库吗？
以上输出在我的终端上。我使用的是MacOS10.7。x、 我有Python 2.7。1，并按照本教程获得Beautiful Soup和lxml，它们都已成功安装，并可使用位于此处的单独测试文件工作。在导致此错误的Python脚本中，我包含了这一行：，在pageCrawler文件中，我包含了以下两行： 如果您能帮助我们找出问题所在以及如何解决问题，我们将不胜感激。
-
DBMS B+树主要内容：B+树的结构,在B+树中搜索记录,B+树插入,B+树删除B+树 是一个平衡的二叉搜索树，它遵循多级索引格式。 在B+树中，叶节点表示实际的数据指针，B+树确保所有叶节点保持在相同的高度。 在B+树中，叶节点使用链表链接，因此，B+树可以支持随机访问以及顺序访问。 B+树的结构 在B+树中，每个叶节点与根节点的距离相等。B+树的顺序为，其中对于每个树是固定的。 它包含内部节点和叶节点。 内部节点 B+树的内部节点可以包含除根节点之外的至少 n/2 个记录
-
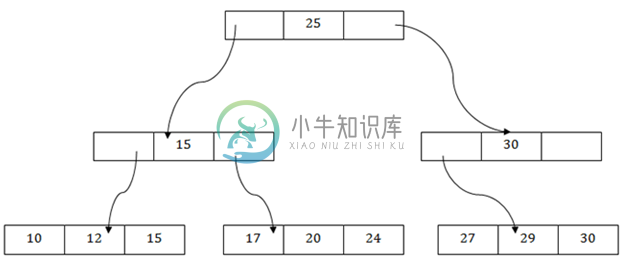
DBMS B+树文件组织B+树文件组织是索引顺序访问方法的高级方法，它使用树状结构在文件中存储记录。 它使用与概念相同，其中主键用于对记录进行排序。 对于每个主键，将生成索引的值并与记录一起映射。 B+树类似于二叉搜索树(BST)，但它可以有两个以上的子节点。 在此方法中，所有记录仅存储在叶节点处，中间节点充当指向叶节点的指针，它们不包含任何记录。 上面 B+树 的描述： 树有一个根节点，即25。 存在具有节点的中间层。
-
XML DOM节点树在本章中，我们将学习XML DOM节点树。 在XML文档中，信息以层次结构组织和维护; 这种分层结构称为节点树。 此层次结构允许开发人员在树周围导航以查找特定信息，从而允许节点访问。 然后可以更新这些节点的内容。 节点树的结构以根元素开始，并扩展到子元素，直到最低级别。 示例 下面的示例演示了一个简单的XML文档，结构树的结构如下图所示 - 从以上示例中可以看出，用图形表示(DOM)如下所示 -
-
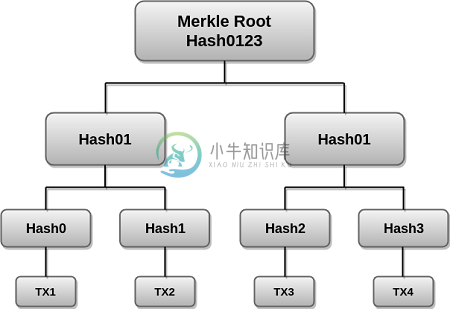
区块链Merkle树Merkle树是区块链技术的基本组成部分。它是由不同数据块的散列组成的数学数据结构，用作块中所有交易的摘要。它还允许对大量数据中的内容进行有效和安全的验证。此结构有助于验证数据的一致性和内容。比特币和以太坊都使用Merkle树结构。Merkle树也被称为哈希树。 Merkle树的概念以1979年为该概念申请专利的Ralph Merkle命名。从根本上说，Merkle树是数据结构树，其中每个叶节点都
-
树型结构目录在树结构的目录系统中，任何目录条目都可以是文件或子目录。 树结构的目录系统克服了两级目录系统的缺点。 现在可以将类似的文件分组到一个目录中。 每个用户都有自己的目录，并且不能进入其他用户的目录。 但是，用户有权读取根数据，但他不能写入或修改此数据。 只有系统管理员才能完全访问根目录。 在这个目录结构中搜索更有效率。 使用当前工作目录的概念。 一个文件可以通过两种类型的路径访问，无论是相对的还是绝对
-
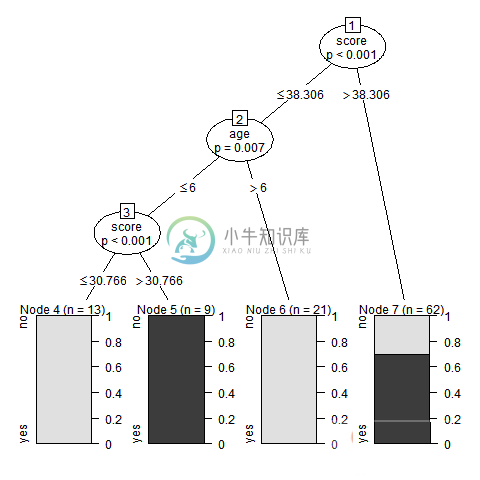
R语言决策树主要内容：安装R包,语法,输入数据,例子决策树是以树的形式表示选择及其结果的图形。图中的节点表示事件或选择，并且图形的边缘表示决策规则或条件。它主要用于使用R的机器学习和数据挖掘应用程序。 使用决策的例子是 - 将接收的邮件预测是否为垃圾邮件，根据这些信息中的因素，预测肿瘤是癌症或预测贷款作为良好或不良的信用风险。 通常，使用观察数据也称为训练数据创建模型。 然后使用一组验证数据来验证和改进模型。 R具有用于创建和可视化决策树的包。 对
-
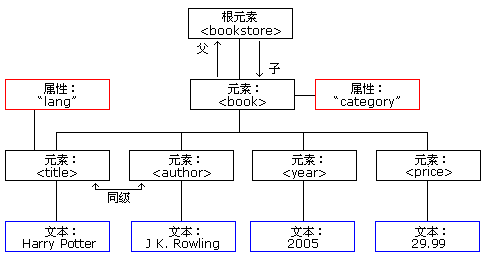
XML 树结构主要内容：一个 XML 文档实例,XML 文档形成一种树结构,实例：,XML 文档实例XML 文档形成了一种树结构，它从"根部"开始，然后扩展到"枝叶"。 一个 XML 文档实例 XML 文档使用简单的具有自我描述性的语法： <?xml version="1.0" encoding="UTF-8"?> <note> <to>Tove</to> <from>Jani</from> <heading>Reminder</heading> <body>Don't forget me th
-
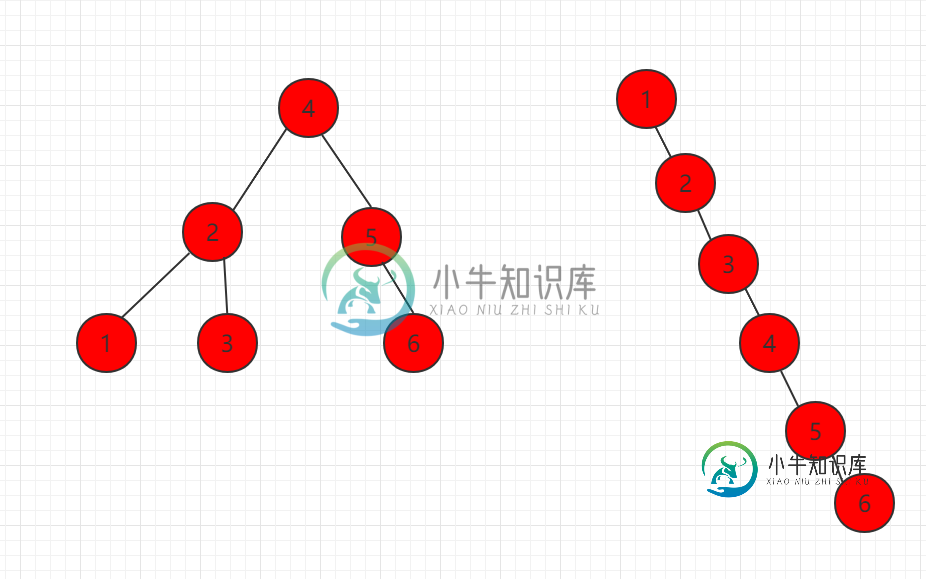二分搜索树的特性一、顺序性 二分搜索树可以当做查找表的一种实现。 我们使用二分搜索树的目的是通过查找 key 马上得到 value。minimum、maximum、successor（后继）、predecessor（前驱）、floor（地板）、ceil（天花板、rank（排名第几的元素）、select（排名第n的元素是谁）这些都是二分搜索树顺序性的表现。 二、局限性 二分搜索树在时间性能上是具有局限性的。 如下图
-
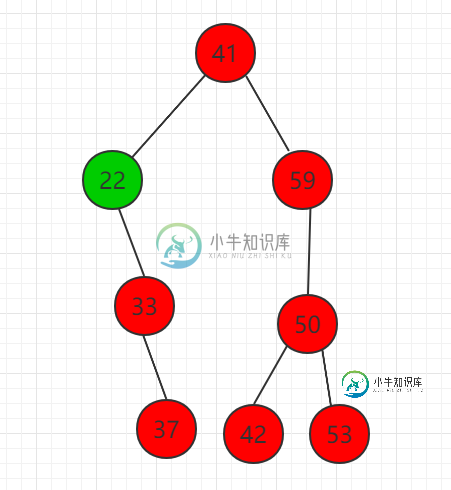二分搜索树节点删除主要内容：src/runoob/binary/BSTRemove.java 文件代码：本小节介绍二分搜索树节点的删除之前，先介绍如何查找最小值和最大值，以及删除最小值和最大值。 以最小值为例（最大值同理）： 查找最小 key 值代码逻辑，往左子节点递归查找下去： ... // 返回以node为根的二分搜索树的最小键值所在的节点 private Node minimum (Node node ) { if ( node. left == null ) retu
-
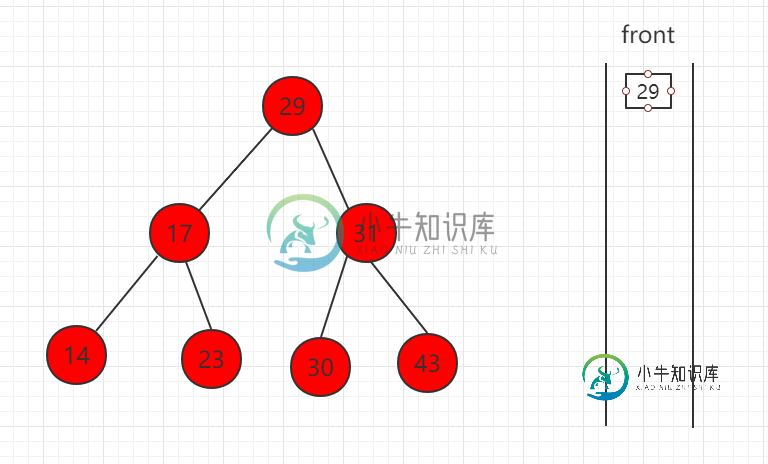二分搜索树层序遍历主要内容：src/runoob/binary/LevelTraverse.java 文件代码：二分搜索树的层序遍历，即逐层进行遍历，即将每层的节点存在队列当中，然后进行出队（取出节点）和入队（存入下一层的节点）的操作，以此达到遍历的目的。 通过引入一个队列来支撑层序遍历： 如果根节点为空，无可遍历； 如果根节点不为空： 先将根节点入队； 只要队列不为空： 出队队首节点，并遍历； 如果队首节点有左孩子，将左孩子入队； 如果队首节点有右孩子，将右孩子入队； 下面依次演示如下步骤： （1）先取出
-
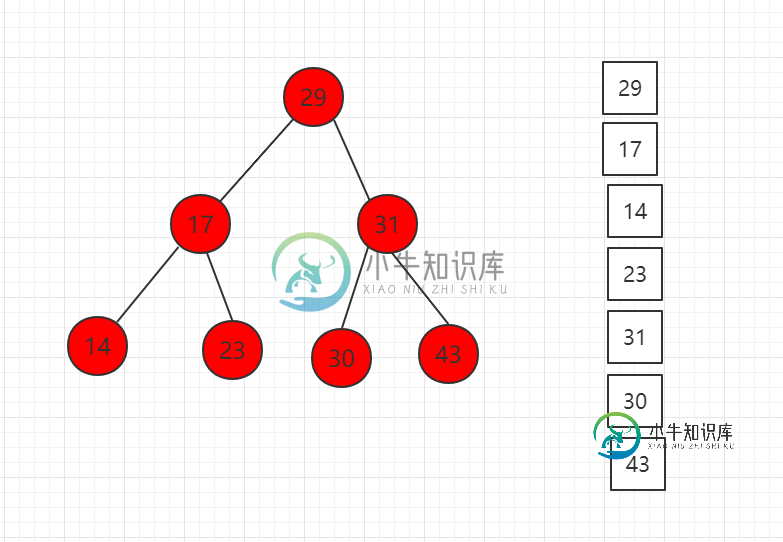二分搜索树深度优先遍历主要内容：src/runoob/binary/Traverse.java 文件代码：二分搜索树遍历分为两大类，深度优先遍历和层序遍历。 深度优先遍历分为三种：先序遍历（preorder tree walk）、中序遍历（inorder tree walk）、后序遍历（postorder tree walk），分别为： 1、前序遍历：先访问当前节点，再依次递归访问左右子树。 2、中序遍历：先递归访问左子树，再访问自身，再递归访问右子树。 3、后序遍历：先递归访问左右子树，再访问自身节
-
二分搜索树节点的查找主要内容：src/runoob/binary/BinarySearchTreeSearch.java 文件代码：二分搜索树没有下标, 所以针对二分搜索树的查找操作, 这里定义一个 contain 方法, 判断二分搜索树是否包含某个元素, 返回一个布尔型变量, 这个查找的操作一样是一个递归的过程, 具体代码实现如下: ... // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法 private boolean contain (Node node, Key key )