《红黑树》专题
-
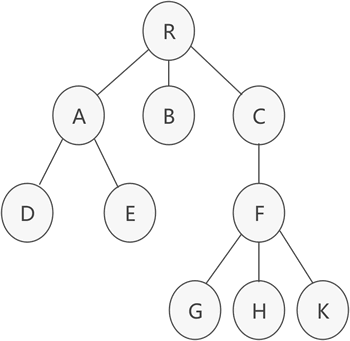 树的孩子兄弟表示法
树的孩子兄弟表示法前面讲解了存储普通树的双亲表示法和孩子表示法,本节来讲解最后一种常用方法—— 孩子兄弟表示法。 图 1 普通树示意图 树结构中,位于同一层的节点之间互为兄弟节点。例如,图 1 的普通树中,节点 A、B 和 C 互为兄弟节点,而节点 D、E 和 F 也互为兄弟节点。 孩子兄弟表示法,采用的是链式存储结构,其存储树的实现思想是:从树的根节点开始,依次用链表存储各个节点的孩子节点和兄弟节点。 因此,该
-
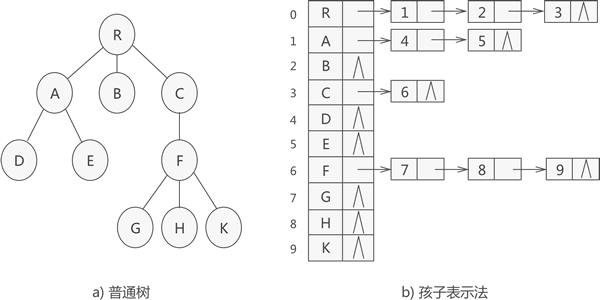 树的孩子表示法
树的孩子表示法前面学习了如何用双亲表示法存储普通树,本节再学习一种存储普通树的方法—— 孩子表示法。 孩子表示法存储普通树采用的是 " 顺序表+ 链表" 的组合结构,其存储过程是:从树的根节点开始,使用顺序表依次存储树中各个节点,需要注意的是,与双亲表示法不同,孩子表示法会给各个节点配备一个链表,用于存储各节点的孩子节点位于顺序表中的位置。 如果节点没有孩子节点(叶子节点),则该节点的链表为空链表。 例如,使用
-
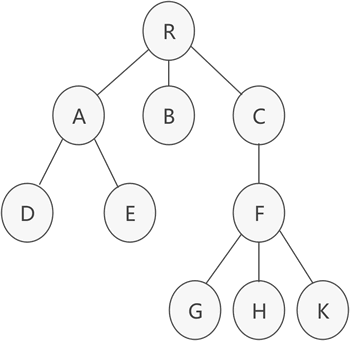 树的双亲表示法
树的双亲表示法前面讲了 二叉树的顺序存储和链式存储,本节来学习如何存储具有普通树结构的数据。 图 1 普通树存储结构 如图 1 所示,这是一棵普通的树,该如何存储呢?通常,存储具有普通树结构数据的方法有 3 种: 双亲表示法; 孩子表示法; 孩子兄弟表示法; 本节先来学习 双亲表示法。 双亲表示法采用顺序表(也就是数组)存储普通树,其实现的核心思想是:顺序存储各个节点的同时,给各节点附加一个记录其父节点位置的变
-
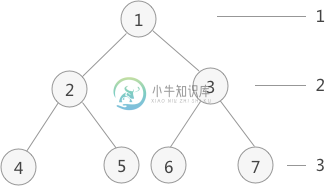 二叉树层次遍历
二叉树层次遍历主要内容:层次遍历的实现过程,实现代码前边介绍了 二叉树的先序、中序和后序的遍历算法,运用了 栈的 数据结构,主要思想就是按照先左子树后右子树的顺序依次遍历树中各个结点。 本节介绍另外一种遍历方式:按照二叉树中的层次从左到右依次遍历每层中的结点。具体的实现思路是:通过使用 队列的数据结构,从树的根结点开始,依次将其左孩子和右孩子入队。而后每次队列中一个结点出队,都将其左孩子和右孩子入队,直到树中所有结点都出队,出队结点的先后顺序就是层
-
 二叉树后序遍历(递归与非递归)
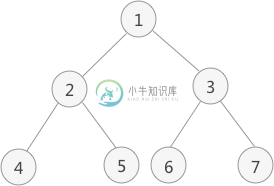
二叉树后序遍历(递归与非递归)主要内容:递归实现,非递归实现二叉树后序遍历的实现思想是:从根节点出发,依次遍历各节点的左右子树,直到当前节点左右子树遍历完成后,才访问该节点元素。 图 1 二叉树 如图 1 中,对此二叉树进行后序遍历的操作过程为: 从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点); 遍历节点 2 的左子树(以节点 4 为根节点); 由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍
-
 二叉树中序遍历(递归和非递归)
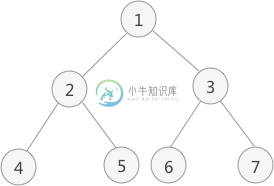
二叉树中序遍历(递归和非递归)主要内容:递归实现,非递归实现二叉树中序遍历的实现思想是: 访问当前节点的左子树; 访问根节点; 访问当前节点的右子树; 图 1 二叉树 以图 1 为例,采用中序遍历的思想遍历该二叉树的过程为: 访问该二叉树的根节点,找到 1; 遍历节点 1 的左子树,找到节点 2; 遍历节点 2 的左子树,找到节点 4; 由于节点 4 无左孩子,因此找到节点 4,并遍历节点 4 的右子树; 由于节点 4 无右子树,因此节点 2 的左子
-
 二叉树先序遍历(递归与非递归)
二叉树先序遍历(递归与非递归)主要内容:递归实现,非递归实现二叉树先序遍历的实现思想是: 访问根节点; 访问当前节点的左子树; 若当前节点无左子树,则访问当前节点的右子树; 图 1 二叉树 以图 1 为例,采用先序遍历的思想遍历该二叉树的过程为: 访问该二叉树的根节点,找到 1; 访问节点 1 的左子树,找到节点 2; 访问节点 2 的左子树,找到节点 4; 由于访问节点 4 左子树失败,且也没有右子树,因此以节点 4 为根节点的子树遍历完成。但节点
-
 二叉树的链式存储结构
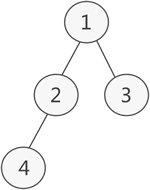
二叉树的链式存储结构上一节讲了 二叉树的顺序存储,通过学习你会发现,其实二叉树并不适合用数组存储,因为并不是每个二叉树都是完全二叉树,普通二叉树使用 顺序表存储或多或多会存在空间浪费的现象。 本节我们学习二叉树的 链式存储结构。 图 1 普通二叉树示意图 如图 1 所示,此为一棵普通的二叉树,若将其采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用 链表存储即可。因此,图 1 对应的链式存储结构如图 2
-
 二叉树的顺序存储结构
二叉树的顺序存储结构二叉树的存储结构有两种,分别为顺序存储和链式存储。本节先介绍 二叉树的顺序存储结构。 二叉树的顺序存储,指的是使用 顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。 因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。 有读者会说,满二叉树也可以使用顺序存储。要知道,满二叉树也是完全二叉树,因为它满足完全二叉树
-
 什么是二叉树
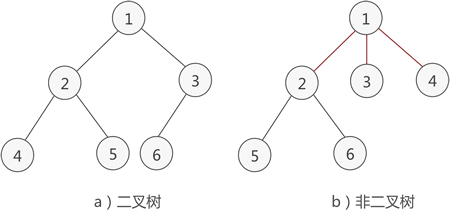
什么是二叉树主要内容:二叉树的性质,满二叉树,完全二叉树,总结通过《 树的存储结构》一节的学习,我们了解了一些树存储结构的基本知识。本节将给大家介绍一类具体的树结构—— 二叉树。 简单地理解,满足以下两个条件的树就是二叉树: 本身是有序树; 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2; 例如,图 1a) 就是一棵二叉树,而图 1b) 则不是。 图 1 二叉树示意图 二叉树的性质 经过前人的总结,二叉树具有以下几个性质: 二叉树中,第 i
-
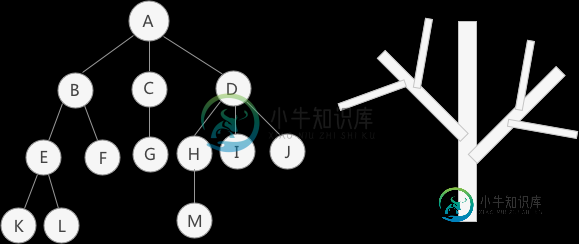 数据结构的树存储结构
数据结构的树存储结构主要内容:树的结点,子树和空树,结点的度和层次,有序树和无序树,森林,树的表示方法,总结之前介绍的所有的 数据结构都是 线性存储结构。本章所介绍的树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合。 (A)
-
Linux查看进程树(pstree命令)
pstree 命令是以树形结构显示程序和进程之间的关系,此命令的基本格式如下: [root@localhost ~]# pstree [选项] [PID或用户名] 表 1 罗列出了 pstree 命令常用选项以及各自的含义。 表 1 pstree命令常用选项及含义 选项 含义 -a 显示启动每个进程对应的完整指令,包括启动进程的路径、参数等。 -c 不使用精简法显示进程信息,即显示的进程中包含子进
-
声纳“测量过滤器作为树状图”颜色显示灰色框而不是绿色框
分析、api、re、web、功能测试、oasisengine、核心 分析sonar.sources=src/main analysis.sonar.tests=src/test analysis.sonar.binaries=target/classes analysis.sonar.junit.reportspath=target/surefire-reports analysis.sonar.
-
使用jsTree检查所有节点后折叠树
我正在使用jsTree显示一个树。我想选择树中可以使用的所有节点。这工作得很好。 但是,这将展开所有节点,并且拥有一个大树将把其余的内容一直往下推。 我想在检查所有节点后折叠树,但使用不起作用。 有人有办法解决吗?
-
jstree记住打开/关闭的树节点
我正在使用jstree来显示/管理一个类别树。我正在使用Ajax调用获取树,并返回以下响应: 我正在使用选项来呈现jstree: 我想记住用户所做的每个操作(打开或关闭任何树节点),因此我绑定了和操作。我遇到的问题是事件没有关于刚刚单击的节点的信息: 我想我错过了,但是jstree docs是相当糟糕的imho和大多数选项甚至没有提到...
