使用 C 查找搜索二叉树中的最长路径

Question

我很难找到使用递归函数查找搜索二叉树的最长路径的代码。

void maxDepth(bst_node *node)
{            ....
}

bst_node是搜索二叉树的节点。

退出递归的条件非常简单：

if(node->leftChild==NULL&&node->rightChild==NULL)
{
return;
}

在进行递归之前，打印节点的值：

printf("%d ",node->value);

如果假设深度x处的节点只有一个左子节点，那么最长路径穿过节点的左子节点，通过使用递归，我们可以这样写：

if(node->rightChld==NULL)
{     
maxDepth(node->leftChild);
}

如果深度x处的节点只有右子节点，则最长路径穿过节点的右子节点，通过使用递归，我们可以像这样编写它

if(node->leftChild==NULL)
{
maxDepth(node->rightChild);

}

但是，如果节点同时具有左子项和右子项怎么办？我不明白我怎么能做到这一点。

例如，对于此二进制搜索树，输出应为：

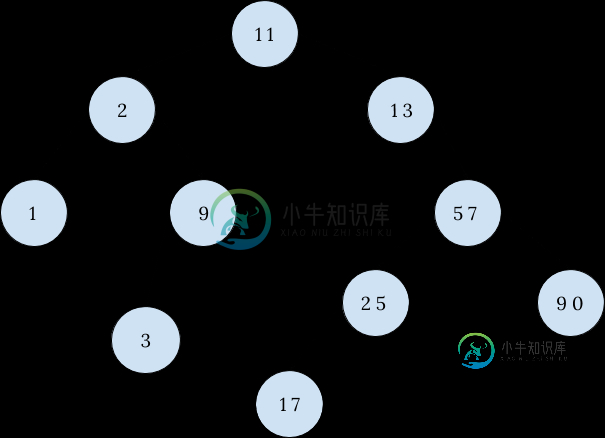
"11 13 57 25 17"

感谢帮助。

Answer 1

#define max(a, b) a > b ? a : b

int maxDepth(bst_node *node) {
    if (node == NULL) {
        return 0;
    }
    int max_left = maxDepth(node->leftChild);
    int max_right = maxDepth(node->rightChild);
    return max(max_left, max_right) + 1;
}

Answer 2

诀窍是仔细考虑每个可能的情况。要么是基本情况，要么您需要将其分解为可以通过递归调用解决的较小问题。

int max(int a, int b) { return a > b ? a : b; }

int maxDepth(bst_node *node)
{
  // If the tree is empty, the depth is zero.
  if (!node) return 0;

  // Otherwise it's this node plus the max of the children.
  return 1 + max(maxDepth(node->leftChild), maxDepth(node->rightChild));
}