是否二叉树也是二叉搜索树的问题检查

Question

我正试图解决这个问题,但我遇到了一些麻烦：

在二进制搜索树(BST)中：

• 节点左子树中每个节点的数据值小于该节点的数据值。
• 节点右侧子树中每个节点的数据值大于该节点的数据值。

class Node {
    int data;
    Node left;
    Node right;
}

boolean check(Node root) {   

    //node doesn't have any children
    if (root.left == null && root.right == null) {
        return true;
    }

    boolean leftIsBst = true;
    boolean rightIsBst = true;

    if (root.left != null) {
        leftIsBst = (root.left.data < root.data) && check(root.left);
    }

    if (root.right != null) {
        rightIsBst = (root.right.data > root.data) && check(root.right);
    }

    return leftIsBst && rightIsBst;
}

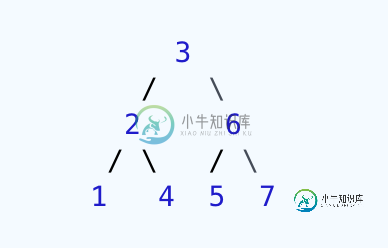
如您所见，节点（4）位于节点（3）的左侧子树中，尽管4大于3，因此方法应该返回false。但是，我的代码返回true。

我怎么能控制这个案子？如何检查左/右子树中的所有值都低于/大于根（不仅是直接子树）？

Answer 1

您的定义是正确的（尽管您不一定需要坚持所有键都是不同的），但是您的代码并没有实现定义中的所有条件。具体地说，您不强制每个子树中的最小值和最大值。

下面是一个实现定义的高效递归解决方案：

boolean check(Node root) {
    return check(root, INT_MIN, INT_MAX);
}
boolean check(Node n, int minval, int maxval) {
    if (n == null) {
        return true;
    }
    return (
        n.data >= minval && n.data <= maxval &&
        check(n.left, minval, n.data-1) &&
        check(n.right, n.data+1, maxval)
    );
}

请注意，我没有在n.data-1和n.data+1中检查溢出，这是您在实际生活中必须做的。如果您希望允许重复键，只需将这些更改为n.data，您就不必担心了。