线性代数

优质

小牛编辑

118浏览

2023-12-01

简单的说，矩阵和数列这两个术语是经常可以替换使用的。更准确地说，矩阵是一个表示线性变换的二维数字数组。矩阵定义下的数学运算是线性代数的主题。

杜勒的魔方

A =
    16     3     2    13
     5    10    11     8
     9     6     7    12
     4    15    14     1

提供了几个例子，给出了MATLAB矩阵运算的一点味道。你已经看到了矩阵转置A'，加一个矩阵到它的转置得到一个对称矩阵。

A + A'

ans =
    32     8    11    17
     8    20    17    23
    11    17    14    26
    17    23    26     2

乘号*表示包括行与列的内积矩阵的乘法。用矩阵去乘它的转置也能得到对称矩阵。

A'*A

ans =
   378   212   206   360
   212   370   368   206
   206   368   370   212
   360   206   212   378

这矩阵的行列式为0，表示该矩阵是奇异阵。

d = det(A)

d =
     0

A的简化行阶梯型不是单位矩阵。

R = rref(A)

R =
     1     0     0     1
     0     1     0    -3
     0     0     1     3
     0     0     0     0

由于矩阵是奇异的，因而它没有逆矩阵。如果你试图计算它的逆：

X = inv(A)

你会得到警告信息：

Warning: Matrix is close to singular or badly scaled.
         Results may be inaccurate. RCOND = 1.175530e-017.

四舍五入的误差从精确奇异性的探测中阻止了矩阵转置的算法。但是rcond的值（表示倒数条件估计）是和eps即浮点相对精度同阶数的，因此计算得的逆不太可能有用。

魔方的特征值很有趣。

e = eig(A)

e =
   34.0000
    8.0000
    0.0000
   -8.0000

特征值之中有一个为零。这是奇异性的另一个结论。最大的特征值为34，为幻和。那是因为元素全为1的向量是特征向量。

v = ones(4,1)

v =
     1
     1
     1
     1

A*v

ans =
    34
    34
    34
    34

当魔方按照它的幻和为比例分配时,

P = A/34

结果是双重随机矩阵，其行与列之和全是1。

P =
    0.4706    0.0882    0.0588    0.3824
    0.1471    0.2941    0.3235    0.2353
    0.2647    0.1765    0.2059    0.3529
    0.1176    0.4412    0.4118    0.0294

这样的矩阵表示转换的概率是一个马尔科夫(Markov)过程。矩阵重复的幂次表示过程重复的步骤。对于我们的例子，第5次方

P^5

是

    0.2507    0.2495    0.2494    0.2504
    0.2497    0.2501    0.2502    0.2500
    0.2500    0.2498    0.2499    0.2503
    0.2496    0.2506    0.2505    0.2493

这表示当k趋于无穷大时，所有元素的k次方P^k趋于1/4。

最后，特征多项式中的系数

poly(A)

是

     1   -34   -64  2176     0

这表明特征多项式

det( A - 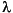I )

是

⁴ - 34³ - 64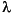² + 2176

常数项是零，因为矩阵是奇异的，立方项系数是-34，因为矩阵是魔方！