隐式评价和基于物品的过滤算法 - Slope One算法
还有一种比较流行的基于物品的协同过滤算法,名为Slope One,它最大的优势是简单,因此易于实现。
Slope One算法是在一篇名为《Slope One:基于在线评分系统的协同过滤算法》的论文中提出的,由Lemire和Machlachlan合著。这篇论文非常值得一读。
我们用一个简单的例子来了解这个算法。假设Amy给PSY打了3分,Whitney Houston打了4分;Ben给PSY打了4分。我们要预测Ben会给Whitney Houston打几分。
用表格来描述这个问题即:
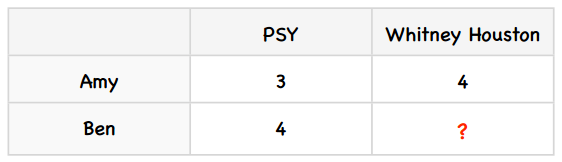
我们可以用以下逻辑来预测Ben对Whitney Houston的评分:由于Amy给Whitney Houston打的分数要比PSY的高一分,所以我们预测Ben也会给高一分,即给到5分。
其实还有其他形式的Slope One算法,比如加权的Slope One。
我们说过Slope One的优势之一是简单,下面说的加权的Slope One看起来会有一些复杂,但是只要耐心地看下去,事情就会变得很清晰了。
你可以将Slope One分为两个步骤:
首先需要计算出两两物品之间的差值(可以在夜间批量计算)。在上文的例子中,这个步骤就是得出Whitney Houston要比PSY高一分。
第二步则是进行预测,比如一个新用户Ben来到了我们网站,他从未听过Whitney Houston的歌曲,我们想要预测他是否喜欢这位歌手。
通过利用他评价过的歌手以及我们计算好的歌手之间的评分差值,就可以进行预测了。
第一步:计算差值
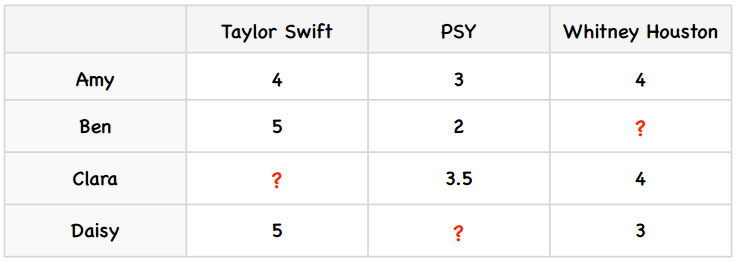
我们先为上述例子增加一些数据:
计算物品之间差异的公式是:
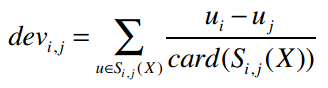
其中,card(S)表示S中有多少个元素;X表示所有评分值的集合;card(Sj,i(X))则表示同时评价过物品j和i的用户数。
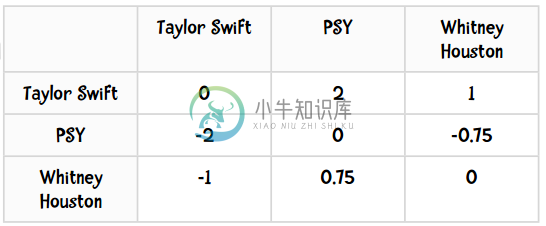
我们来考察PSY和Taylor Swift之间的差值,card(Sj,i(X))的值是2——因为有两个用户(Amy和Ben)同时对PSY和Taylor Swift打过分。
分子uj-ui表示用户对j的评分减去对i的评分,代入公式得:
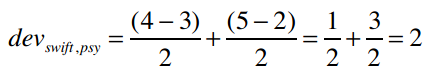
所以PSY和Taylor Swift的差异是2,即用户们给Taylor Swift的评分比PSY要平均高出两分。那Taylor Swift和PSY的差异呢?
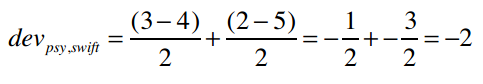
作业:计算其他物品之间的差值
头脑风暴
试想我们的音乐站点有100万个用户对20万个歌手做评价。如果有一个新进的用户对10个歌手做了评价,我们是否需要重新计算20万×20万的差异数据,或是有其他更简单的方法?

答案是你不需要计算整个数据集,这正是Slope One的美妙之处。对于两个物品,我们只需记录同时评价过这对物品的用户数就可以了。
比如说Taylor Swift和PSY的差值是2,是根据9位用户的评价计算的。当有一个新用户对Taylor Swift打了5分,PSY打了1分时,更新后的差值为:
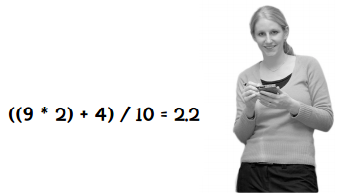
第二步:使用加权的Slope One算法进行预测
好,现在我们有了物品之间的差异值,下面就用它来进行预测。这里我们将使用加权的Slope One算法来进行预测,用PWS1来表示,公式为:
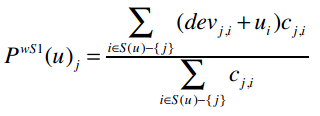
其中:
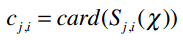
PWS1(u)j表示我们将预测用户u对物品i的评分。比如PWS1(Ben)Whitney Houston表示Ben对Whitney Houston的预测评分。下面就让我们来求解这个问题。
首先来看分子:
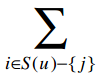
表示遍历Ben评价过的所有歌手,除了Whitney Houston以外(也就是-{j}的意思)。
整个分子的意思是:对于Ben评价过的所有歌手(Whitney Houston除外),找出Whitney Houston和这些歌手之间的差值,并将差值加上Ben对这个歌手的评分。
同时,我们要将这个结果乘以同时评价过两位歌手的用户数。
让我们分解开来看,先将Ben的评分情况和两两歌手之间的差异值展示如下:
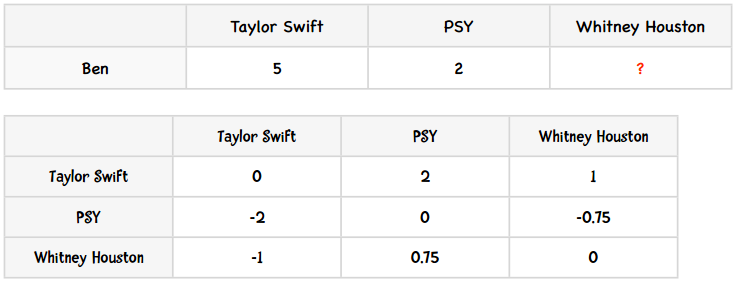
- Ben对Taylor Swift打了5分,也就是ui
- Whitney Houston和Taylor Swift的差异是-1,即devj,i
- devj,i + ui = 4
- 共有两个用户(Amy和Daisy)同时对Taylor Swift和Whitney Houston做了评价,即cj,i = 2
- 那么(devj,i + ui) cj,i = 4 × 2 = 8
- Ben对PSY打了2分
- Whitney Houston和PSY的差异是0.75
- devj,i + ui = 2.75
- 有两个用户同时评价了这两位歌手,因此(devj,i + ui) cj,i = 2.75 × 2 = 5.5
- 分子:8 + 5.5 = 13.5
- 分母:2 + 2 = 4
- 预测评分:13.5 ÷ 4 = 3.375


