《算法优化》专题
-
 基数排序算法
基数排序算法主要内容:基数排序算法的实现细节,基数排序算法的代码实现在学会 计数排序算法的基础上,本节我们再学习一种排序算法,称为 基数排序算法。 基数排序算法适用于对多个整数或者多个字符串进行升序或降序排序,例如: 121, 432, 564, 23, 1, 45, 788 "zhangsan"、"lisi"、"wangwu" 一个整数由多个数字组成,例如 123 由 1、2、3 这 3 个数字组成;一个字符串由多个字符组成,例如 "lisi" 由 "l"、"i
-
 计数排序算法
计数排序算法主要内容:计数排序算法的实现思路,计数排序算法的具体实现通过统计序列中各个元素出现的次数,完成对整个序列的升序或降序排序,这样的排序算法称为 计数排序算法。 接下来,我们为您系统地讲解计数排序算法。 计数排序算法的实现思路 假设待排序序列为 {4, 2, 2, 8, 3, 3, 1},使用计数排序算法完成升序排序的过程为: 1) 找到序列中的最大值(用 max 表示)。对于 {4, 2, 2, 8, 3, 3, 1} 序列来说,最大值是 8。 2) 创
-
 快速排序算法
快速排序算法主要内容:快速排序算法的实现提到排序算法,多数人最先想到的就是快速排序算法。快速排序算法是在分治算法基础上设计出来的一种排序算法,和其它排序算法相比,快速排序算法具有效率高、耗费资源少、容易实现等优点。 快速排序算法的实现思路是: 从待排序序列中任选一个元素(假设为 pivot)作为中间元素,将所有比 pivot 小的元素移动到它的左边,所有比 pivot 大的元素移动到它的右边; pivot 左右两边的子序列看作是两个待排
-
 归并排序算法
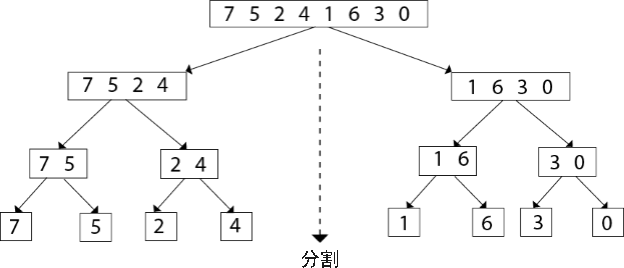
归并排序算法主要内容:归并排序算法的具体实现归并排序算法是在 分治算法基础上设计出来的一种排序算法,它可以对指定序列完成升序(由小到大)或降序(由大到小)排序,对应的时间复杂度为 。 归并排序算法实现排序的思路是: 将整个待排序序列划分成多个不可再分的子序列,每个子序列中仅有 1 个元素; 所有的子序列进行两两合并,合并过程中完成排序操作,最终合并得到的新序列就是有序序列。 举个简单的例子,使用归并排序算法对 {7, 5, 2, 4, 1,
-
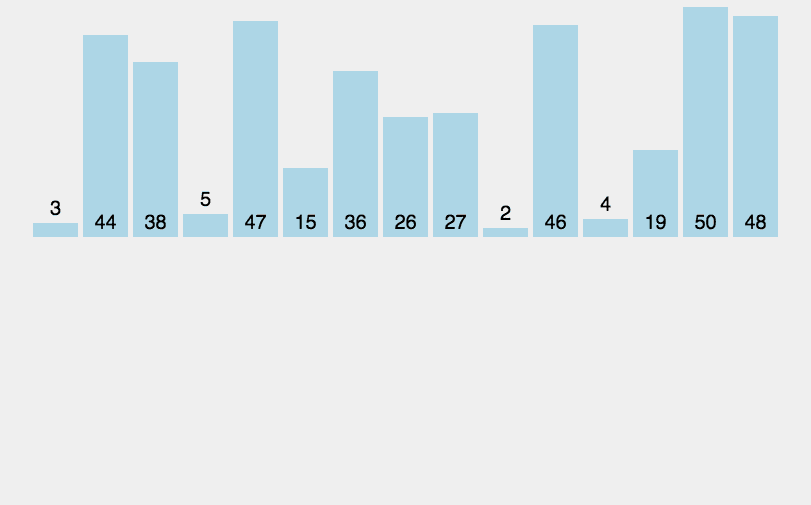 希尔排序算法
希尔排序算法主要内容:序列的划分方法,希尔排序算法的具体实现前面给大家介绍了 插入排序算法,通过将待排序序列中的元素逐个插入到有序的子序列中,最终使整个序列变得有序。下图所示的动画演示了插入排序的整个过程: 图 1 插入排序算法 观察动画不难发现,插入排序算法是通过比较元素大小和交换元素存储位置实现排序的,比较大小和移动元素的次数越多,算法的效率就越差。 希尔排序算法又叫 缩小增量排序算法,是一种更高效的插入排序算法。和普通的插入排序算法相比,希尔排序算法
-
 选择排序算法
选择排序算法主要内容:选择排序算法的具体实现对数据量较少的序列实现升序或降序排序,可以考虑使用 选择排序算法,它对应的时间复杂度为 。 排序排序算法对含有 n 个元素的序列实现排序的思路是:每次从待排序序列中找出最大值或最小值,查找过程重复 n-1 次。对于每次找到的最大值或最小值,通过交换元素位置的方式将它们放置到适当的位置,最终使整个序列变成有序序列。 举个例子,我们使用选择排序算法对 {14, 33, 27, 10, 35, 19,
-
 插入排序算法
插入排序算法主要内容:插入排序算法的具体实现插入排序算法可以对指定序列完成升序(从小到大)或者降序(从大到小)排序,对应的时间复杂度为 。 插入排序算法的实现思路是:初始状态下,将待排序序列中的第一个元素看作是有序的子序列。从第二个元素开始,在不破坏子序列有序的前提下,将后续的每个元素插入到子序列中的适当位置。 举个简单的例子,用插入排序算法对 {14, 33, 27, 10, 35, 19, 42, 44} 实现升序排序的过程如下: 1)
-
 冒泡排序算法
冒泡排序算法主要内容:冒泡排序算法的具体实现冒泡排序是所有排序算法中最简单、最易实现的算法,有时也称为起泡排序算法。 使用冒泡排序算法对 n 个数据进行排序,实现思路是:从待排序序列中找出一个最大值或最小值,这样的操作执行 n-1 次,最终就可以得到一个有序序列。 举个例子,对 {14, 33, 27, 35, 10} 序列进行升序排序(由小到大排序),冒泡排序算法的实现过程是: 从 {14, 33, 27, 35, 10} 中找到最大值
-
动态规划算法
主要内容:动态规划算法的实际应用动态规划算法解决问题的过程和分治算法类似,也是先将问题拆分成多个简单的小问题,通过逐一解决这些小问题找到整个问题的答案。不同之处在于,分治算法拆分出的小问题之间是相互独立的,而动态规划算法拆分出的小问题之间相互关联,例如要想解决问题 A,必须先解决问题 B 和 C。 《贪心算法》一节中,给大家举过一个例子,假设有 1、7、10 这 3 种面值的纸币,每种纸币使用的数量不限,要求用尽可能少的纸币拼凑
-
 顺序查找算法
顺序查找算法主要内容:顺序查找的实现,顺序查找的性能分析,总结通过前面对静态 查找表的介绍,静态查找表即为只做查找操作的查找表。 静态查找表既可以使用顺序表表示,也可以使用链表结构表示。虽然一个是数组、一个链表,但两者在做查找操作时,基本上大同小异。 本节以静态查找表的顺序存储结构为例做详细的介绍。 顺序查找的实现 静态查找表用顺序存储结构表示时,顺序查找的查找过程为:从表中的最后一个数据元素开始,逐个同记录的关键字做比较,如果匹配成功,则查找成功;反之,如
-
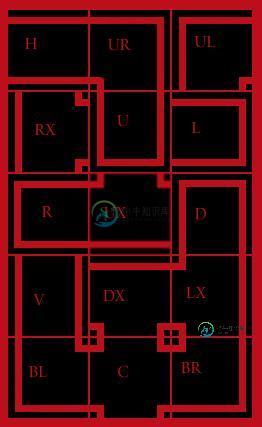 PCG伪马泽算法?
PCG伪马泽算法?我使用photoshop创建了一组瓷砖: 我正在寻找一种方法来填充这些80x80瓷砖的屏幕,其中大多数区域是相连的。这是一个吃豆人风格游戏的游戏板,而不是一个有入口和出口的迷宫。 我唯一的目标是永远不要有一个面向墙壁的开口。 我目前通过从基于上一个瓷砖的子集中随机选择下一个瓷砖来实现这一点,因此如果最后一个瓷砖左侧有墙,那么下一个砖就不能左侧有开口。我还将拐角限制为较小的子集。这只适用于第一行。
-
浮点整数算法
我的问题是,是否有一种方法可以在不通过堆栈的情况下完成所有这些操作。x86_64是否有将xmm0的内容复制到eax或其他通用寄存器的内插? 编辑:问题本身在讨论过程中发生了变化。最后有两个备注,在这两个备注中,我都引用了Intel C++复杂参考的相应部分。 > 可以使用intrinsics在通用Regiter和XMM寄存器之间移动数据(“Steaming SIMD Extensions->流式S
-
log4j2新压缩算法
我希望使用log4j2 RollingFileAppender和定制的压缩算法(ZStd)。 目前为止支持的压缩算法似乎是FileExtension枚举(zip,gz,bz2,...)中的压缩算法,请参见https://github.com/apache/logging-log4j2/blob/efa64bfad3f67c5b5fed6b25d65ef5ca2212011b/log4j-core/
-
7.21.Dijkstra 算法分析
最后,让我们看看 Dijkstra 算法的运行时间。我们首先注意到,构建优先级队列需要 $$O(V)$$ 时间,因为我们最初将图中的每个顶点添加到优先级队列。 一旦构造了队列,则对于每个顶点执行一次 while 循环,因为顶点都在开始处添加,并且在那之后才被移除。 在该循环中每次调用 delMin,需要 $$O(logV)$$时间。 将该部分循环和对 delMin 的调用取为 $$O(Vlog(V
-
08-JavaScrpit-算法应用
基本排序算法
