《变换》专题
-
 OpenCV拉普拉斯变换
OpenCV拉普拉斯变换拉普拉斯(Laplacian)操作也是一个派生的操作,用来找出图像中的边缘。 这是一个二阶导数掩模。 在这个隐藏中,我们有两个进一步的分类,一个是正拉普拉斯操作,另一个是负拉普拉斯操作。 与其他算子不同,拉普拉斯并没有在任何特定方向上取出边缘,而是在后续分类中取出边缘。 向内边缘 向外边缘 可以使用类的方法对图像执行拉普拉斯变换操作,以下是此方法的语法。 该方法接受以下参数 - src - 表示源
-
用变量替换文本
问题内容: 我怎样才能做到这一点? 它将替换为文本。但是我想用变量的内容替换它。 我尝试过 它也不起作用。 问题答案: 您需要使用双引号: 您的单引号可防止将shell变量替换为其内容。
-
第 18 章: Monad变换器
动机: 避免样板代码 Monad提供了一种强大途径以构建带效果的计算。虽然各个标准monad皆专一于其特定的任务,但在实际代码中,我们常常想同时使用多种效果。 比如,回忆在第十章中开发的 Parse 类型。在介绍monad之时,我们提到这个类型其实是乔装过的 State monad。事实上我们的monad比标准的 State monad 更加复杂:它同时也使用了 Either 类型来表达解析过程中
-
3D矩阵透视变换
问题内容: 我正在使用阴影中的形状生成使用安装在移动平台上的相机拍摄的图像的数字地形模型(DTM)。用Python编写的算法似乎运行得很好,但是输出是倾斜的并且有点球形,所以我怀疑我需要从DTM中消除透视失真和桶形。 如果有人对此感兴趣,可以在这里获得数据。 摄像机以41度倾斜安装,并具有以下摄像机和失真矩阵: 如何应用透视变换并从此矩阵中消除桶形失真以获得平坦的DTM? 我已经尝试过使用Open
-
对数极坐标变换
我正在尝试对图像执行对数极坐标变换,以便进行图像配准。换句话说,我正在努力实现这一点:输入图像- 我需要用Java从头开始编写代码,因为我将使用OpenCL Java绑定在GPU端完成这项工作,而不能使用库。这方面有多个线程,但没有一个能真正帮助我,主要是因为它们都使用内置的MATLAB函数,我无法复制。 为了让它发挥作用,我一直在尝试Polar Transform而不是Log-Polar Tra
-
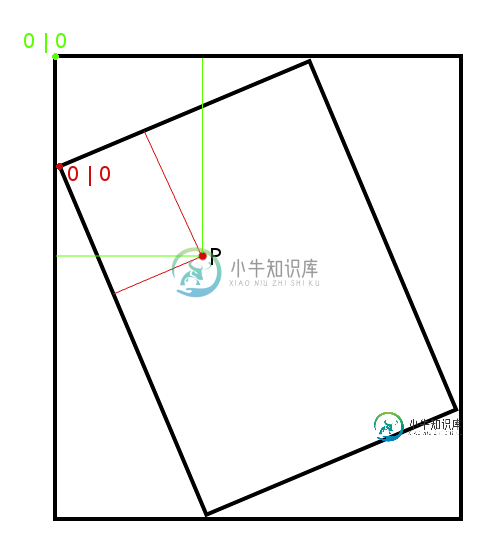 Java:坐标变换 - 旋转
Java:坐标变换 - 旋转给定的是一个旋转的矩形,该矩形内接到另一个矩形中<两个矩形都有自己的坐标系 在该区域中 我对变换矩阵的尝试(setRotate() 如何计算P点相对于外矩形的位置? 提前感谢!
-
互斥JSON的Jolt变换
-
Json阵列变换与Jolt
我正在尝试使用 Jolt 从一个 JSON 数组转换为另一个数组。它由一个没有键的嵌套 JSON 数组组成。 这是我的意见: 我想得到以下输出: 我能够使用此规范文件为单个嵌套数组元素添加键: 但我不知道如何将此应用于外部JSON数组。
-
颠簸变换 JSON 数组
我需要Jolt转换的帮助。我有数组,由许多json对象组成。(https://jolt-demo.appspot.com/) Jolt需要进行哪些转换才能获得以下结果? 现在我有了下一个Jolt构造: 但以下结果不正确:
-
液基生成变换器
难道没有任何工具或命令行可以自动创建changelog文件吗?我使用的JHipster可以正确地为新实体创建changelogs,但正如这里所说的,JHipster不会为更新的实体生成新的changelogs,所以我想知道它们是否是生成额外changelogs的工具?实际上,我是通过手工编写xml文件来创建changelogs,这似乎并不是非常高效。 谢谢你的阅读。
-
docx4j用html替换变量
有没有办法做到这一点?
-
2.2.2 坐标系和变换
在文档 场景编辑器 和 节点和组件 中,我们介绍了可以通过 变换工具 和编辑 属性检查器 中节点的属性来变更节点的显示行为。这篇文档我们将会深入了解节点所在场景空间的坐标系,以及节点的 位置(Position)、旋转(Rotation)、缩放(Scale)、尺寸(Size) 四大变换属性的工作原理。而 3D 节点相比 2D 节点,在变换属性的 API 用法上做了一些改动,具体内容可参考 3D 节点
-
4.12 霍夫直线变换
目标 我们将理解霍夫变换的概念。 我们将看到如何使用它来检测图像中的线条。 我们将看到以下函数:cv2.HoughLines(),cv2.HoughLinesP() 理论基础 霍夫变换是一种用来检测形状的流行的技术,如果你能以数学形式来表示这种形状的话。它可以检测到形状,即使它被破坏或扭曲了一点。我们将看到它是如何检测出一条线。 一条线可以表示为 $y = mx+c$,或以参数方程表示,$\rho
-
第八课 缩放变换
缩放矩阵也很简单!它的作用是放大或缩小物体的尺寸!在很多情况下,你可能想对某些对象做这些处理,例如,当你想用同一模型产生一些差异(大树和小树本质上是一样的),亦或你想将物体的尺寸与其现实世界的尺寸联系起来!对于上面的例子,你可能想使点的三个坐标分量进行相同的缩放。然而,有时候你可能只想缩放两个坐标轴上的分量,导致模型变“厚”或“薄”。 计算变换矩阵是非常复杂的!我们从单位矩阵开始,记住它与向量相乘
-
第七课 旋转变换
接下来的变换是旋转变换,就是说给定一个角度和点,我们将点绕着一个坐标轴旋转。在旋转过程中发生变化的总是x,y,z三个坐标里面的其中两个,而不让第三个坐标值变化。这意味着,旋转路径总在三个坐标轴平面中的一个之中:绕 Z 轴的是 xy 面、绕 X 轴的是 yz 面、绕 Y 轴的是 xy 面。还有许多复杂的旋转变换可以让你绕任意一个向量旋转,但是眼下我们并不需要讨论这些。 让我们概括地定义这个问题这个问
