Algorithms

机器学习算法可大致分为两种类型 - Supervised和非Unsupervised 。 本章将详细讨论它们。

监督学习

该算法由目标或结果或因变量组成，该变量是从给定的一组预测变量或自变量预测的。 使用这些变量集，我们生成一个将输入变量映射到所需输出变量的函数。 训练过程一直持续到模型在训练数据上达到所需的准确度。

监督学习的例子 - 回归，决策树，随机森林，KNN，Logistic回归等。

无监督学习

在该算法中，没有目标或结果或因变量来预测或估计。 它用于将给定数据集聚类到不同的组中，广泛用于将客户划分为不同的组以进行特定干预。 Apriori算法和K-means是无监督学习的一些例子。

强化学习

使用该算法，机器经过训练以做出具体决定。 在这里，算法通过使用试错法和反馈方法不断训练自己。 该机器从过去的经验中学习，并尝试捕获最佳可能的知识，以做出准确的业务决策。

马尔可夫决策过程是强化学习的一个例子。

常用机器学习算法列表

以下是几乎可用于任何数据问题的常用机器学习算法列表 -

• 线性回归
• Logistic Regression
• 决策树
• SVM
• 朴素贝叶斯
• KNN
• K-Means
• 随机森林
• 降维算法
• Gradient Boosting算法，如GBM，XGBoost，LightGBM和CatBoost

本节详细讨论了每一个 -

线性回归

线性回归用于基于连续变量估计真实世界值，例如房屋成本，呼叫数量，总销售额等。 在这里，我们通过拟合最佳线来建立依赖变量和自变量之间的关系。 这条最佳拟合线称为regression line ，由线性方程Y= a *X + b 。

在这个等式中 -

Y - 因变量

a - 坡度

X - 自变量

b - 拦截

这些系数a和b是基于最小化数据点和回归线之间的距离的平方差的总和而导出的。

例子 (Example)

理解线性回归的最佳方法是考虑一个例子。 假设我们被要求按照其权重的递增顺序安排学生上课。 通过观察学生并在视觉上分析他们的高度和构建，我们可以根据需要使用这些参数（高度和构建）的组合来安排它们。 这是现实世界的线性回归示例。 我们已经发现高度和构造通过关系与权重相关，这看起来类似于上面的等式。

线性回归的类型

线性回归主要有两种类型 - Simple Linear Regression和Multiple Linear Regression 。 简单线性回归的特征在于一个独立变量，而多元线性回归的特征在于多个独立变量。 在找到最佳拟合线时，您可以拟合多项式或曲线回归。 您可以使用以下代码来实现此目的。

import matplotlib.pyplot as plt
plt.scatter(X, Y)
yfit = [a + b * xi for xi in X]
plt.plot(X, yfit)

构建线性回归器

回归是估计输入数据和连续值输出数据之间关系的过程。 这些数据通常采用实数形式，我们的目标是估计控制从输入到输出的映射的基础函数。

考虑输入和输出之间的映射，如图所示 -

1 --> 2
3 --> 6
4.3 --> 8.6
7.1 --> 14.2

通过分析模式，您可以轻松估计输入和输出之间的关系。 我们可以观察到输出是每种情况下输入值的两倍，因此转换将是 - f(x) = 2x

线性回归是指使用输入变量的线性组合来估计相关函数。 前面的示例是一个由一个输入变量和一个输出变量组成的示例。

线性回归的目标是提取将输入变量与输出变量相关联的相关线性模型。 这旨在使用线性函数最小化实际输出和预测输出之间的差的平方和。 这种方法称为Ordinary Least Squares 。 您可以假设那里的弯曲线更适合这些点，但线性回归不允许这样做。 线性回归的主要优点是它并不复杂。 您也可以在非线性回归中找到更准确的模型，但它们会更慢。 这里，模型尝试使用直线近似输入数据点。

让我们了解如何在Python中构建线性回归模型。

请考虑为您提供了一个名为data_singlevar.txt的数据文件。 它包含以逗号分隔的行，其中第一个元素是输入值，第二个元素是与此输入值对应的输出值。 你应该使用它作为输入参数 -

假设最适合一组积分的线是 -

y = a + b * x

其中b =（sum（xi * yi） - n * xbar * ybar）/ sum（（xi - xbar）^ 2）

a = ybar - b * xbar

为此目的使用以下代码 -

# sample points
X = [0, 6, 11, 14, 22]
Y = [1, 7, 12, 15, 21]
# solve for a and b
def best_fit(X, Y):
   xbar = sum(X)/len(X)
   ybar = sum(Y)/len(Y)
   n = len(X) # or len(Y)
   numer = sum([xi*yi for xi,yi in zip(X, Y)]) - n * xbar * ybar
   denum = sum([xi**2 for xi in X]) - n * xbar**2
   b = numer/denum
   a = ybar - b * xbar
   print('best fit line:\ny = {:.2f} + {:.2f}x'.format(a, b))
   return a, b
# solution
a, b = best_fit(X, Y)
#best fit line:
#y = 0.80 + 0.92x
# plot points and fit line
import matplotlib.pyplot as plt
plt.scatter(X, Y)
yfit = [a + b * xi for xi in X]
plt.plot(X, yfit)
plt.show()
best fit line:
y = 1.48 + 0.92x

如果运行上面的代码，您可以观察输出图形，如图所示 -

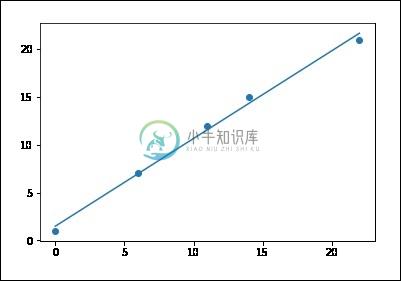
请注意，此示例仅使用糖尿病数据集的第一个特征，以说明此回归技术的二维图。 在图中可以看到直线，显示线性回归如何尝试绘制直线，这将最好地最小化数据集中观察到的响应之间的残差平方和线性近似预测的响应。

您可以使用下面显示的程序代码计算系数，残差平方和方差分数 -

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the diabetes dataset
diabetes = datasets.load_diabetes()
# Use only one feature
diabetes_X = diabetes.data[:, np.newaxis, 2]
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-30]
diabetes_X_test = diabetes_X[-30:]
# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-30]
diabetes_y_test = diabetes.target[-30:]
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean squared error
print("Mean squared error: %.2f" 
      % mean_squared_error(diabetes_y_test, diabetes_y_pred))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color = 'black')
plt.plot(diabetes_X_test, diabetes_y_pred, color = 'blue', linewidth = 3)
plt.xticks(())
plt.yticks(())
plt.show()

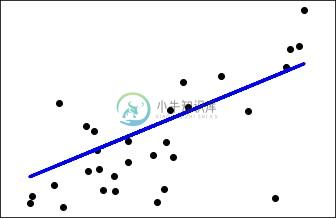
执行上面给出的代码后，您可以观察到以下输出 -

Automatically created module for IPython interactive environment
('Coefficients: \n', array([ 941.43097333]))
Mean squared error: 3035.06
Variance score: 0.41

Logistic回归

逻辑回归是机器学习从统计学中借用的另一种技术。 它是二进制分类问题的首选方法，即两个类值的问题。

它是一种分类算法，而不是名称所示的回归算法。 它用于根据给定的自变量集估计离散值或值，如0/1，Y/N，T/F. 它通过将数据拟合到logit函数来预测事件发生的概率。 因此，它也被称为logit regression 。 因为，它预测概率，其输出值介于0和1之间。

例子 (Example)

让我们通过一个简单的例子来理解这个算法。

假设有一个难题要解决，只有2个结果场景 - 要么有解决方案要么没有解决方案。 现在假设，我们有各种各样的谜题来测试一个人擅长哪些科目。 结果可能是这样的 - 如果给出三角拼图，一个人可能有80％的可能解决它。 另一方面，如果给出地理谜题，那么该人可能只有20％可能解决它。 这是Logistic回归有助于解决的问题。 根据数学，结果的对数几率表示为预测变量的线性组合。

odds = p/ (1-p) = probability of event occurrence/probability of not event occurrence
ln(odds) = ln(p/(1-p)) ; ln is the logarithm to the base ‘e’.
logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk

注意，在上面的p是存在感兴趣特征的概率。 它选择的参数最大化观察样本值的可能性，而不是最小化误差平方和（如普通回归）。

请注意，记录日志是复制步进函数的最佳数学方法之一。

在进行逻辑回归时，以下几点值得注意 -

• 它与回归类似，其目的是找到权衡每个输入变量的系数的值。

• 与线性回归不同，使用称为逻辑函数的非线性函数找到输出的预测。

• 逻辑函数看起来像一个大'S'并且会将任何值更改为0到1的范围。这很有用，因为我们可以将规则应用于逻辑函数的输出，以将值分配给0和1并预测类值。

• 学习逻辑回归模型的方式，由它做出的预测也可以用作属于0级或1级的给定数据实例的概率。这对于需要为预测提供更多推理的问题非常有用。 。

• 与线性回归一样，当删除输出变量的不相关属性并删除类似属性时，逻辑回归效果更好。

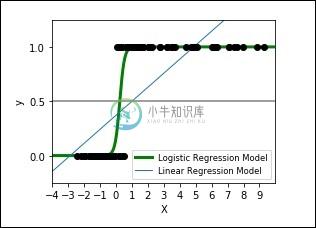
以下代码显示了如何使用逻辑曲线开发逻辑表达式的绘图，其中合成数据集被分类为值0或1，即一类或二类。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# This is the test set, it's a straight line with some Gaussian noise
xmin, xmax = -10, 10
n_samples = 100
np.random.seed(0)
X = np.random.normal(size = n_samples)
y = (X > 0).astype(np.float)
X[X > 0] *= 4
X += .3 * np.random.normal(size = n_samples)
X = X[:, np.newaxis]
# run the classifier
clf = linear_model.LogisticRegression(C=1e5)
clf.fit(X, y)
# and plot the result
plt.figure(1, figsize = (4, 3))
plt.clf()
plt.scatter(X.ravel(), y, color='black', zorder=20)
X_test = np.linspace(-10, 10, 300)
def model(x):
return 1/(1 + np.exp(-x))
loss = model(X_test * clf.coef_ + clf.intercept_).ravel()
plt.plot(X_test, loss, color='blue', linewidth=3)
ols = linear_model.LinearRegression()
ols.fit(X, y)
plt.plot(X_test, ols.coef_ * X_test + ols.intercept_, linewidth=1)
plt.axhline(.5, color='.5')
plt.ylabel('y')
plt.xlabel('X')
plt.xticks(range(-10, 10))
plt.yticks([0, 0.5, 1])
plt.ylim(-.25, 1.25)
plt.xlim(-4, 10)
plt.legend(('Logistic Regression Model', 'Linear Regression Model'),
loc="lower right", fontsize='small')
plt.show()

输出图如下所示 -

决策树算法

它是一种监督学习算法，主要用于分类问题。 它适用于离散和连续因变量。 在该算法中，我们将总体分成两个或更多个同类集。 这是基于最重要的属性来完成的，以尽可能地作为不同的组。

决策树广泛用于机器学习，包括分类和回归。 在决策分析中，决策树用于在视觉上和明确地表示决策和决策。 它使用树状的决策模型。

绘制决策树，其根部位于顶部，分支位于底部。 在图像中，粗体文本表示条件/内部节点，树基于该节点/内部节点分割成分支/边缘。 不再分裂的分支端是决策/叶子。

例子 (Example)

考虑使用泰坦尼克数据集来预测乘客是否能够存活的示例。 下面的模型使用数据集中的3个特征/属性/列，即性别，年龄和sibsp（没有配偶/子女）。 在这种情况下，乘客是否死亡或幸存，分别表示为红色和绿色文本。

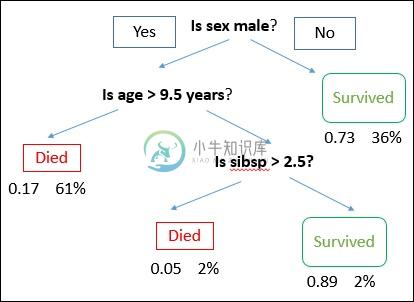
在一些示例中，我们看到基于多个属性将群体分类到不同的群组中以识别“他们是否做某事”。 为了将人口分成不同的异构群体，它使用各种技术，如基尼，信息增益，卡方，熵等。

理解决策树如何工作的最好方法是玩Jezzball--一款来自微软的经典游戏。 基本上，在这个游戏中，你有一个移动墙壁的房间，你需要创建墙壁，以便在没有球的情况下清除最大区域。

因此，每次你用墙隔开房间时，你都试图在同一个房间里创造2个不同的人口。 决策树以非常类似的方式工作，通过将人口分成尽可能不同的群体。

观察下面给出的代码及其输出 -

#Starting implementation
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
%matplotlib inline
from sklearn import tree
df = pd.read_csv("iris_df.csv")
df.columns = ["X1", "X2", "X3","X4", "Y"]
df.head()
#implementation
from sklearn.cross_validation import train_test_split
decision = tree.DecisionTreeClassifier(criterion="gini")
X = df.values[:, 0:4]
Y = df.values[:, 4]
trainX, testX, trainY, testY = train_test_split( X, Y, test_size = 0.3)
decision.fit(trainX, trainY)
print("Accuracy: \n", decision.score(testX, testY))
#Visualisation
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus as pydot
dot_data = StringIO()
tree.export_graphviz(decision, out_file=dot_data)
graph = pydot.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())

Output

Accuracy:
0.955555555556

例子 (Example)

在这里，我们使用钞票认证数据集来了解准确性。

# Using the Bank Note dataset
from random import seed
from random import randrange
from csv import reader
# Loading a CSV file
filename ='data_banknote_authentication.csv'
def load_csv(filename):
   file = open(filename, "rb")
   lines = reader(file)
   dataset = list(lines)
   return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
   for row in dataset:
      row[column] = float(row[column].strip())
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
   dataset_split = list()
   dataset_copy = list(dataset)
   fold_size = int(len(dataset)/n_folds)
   for i in range(n_folds):
      fold = list()
      while len(fold) < fold_size:
         index = randrange(len(dataset_copy))
         fold.append(dataset_copy.pop(index))
      dataset_split.append(fold)
   return dataset_split
# Calculating accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct/float(len(actual)) * 100.0
# Evaluating an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
   folds = cross_validation_split(dataset, n_folds)
   scores = list()
   for fold in folds:
      train_set = list(folds)
      train_set.remove(fold)
      train_set = sum(train_set, [])
      test_set = list()
      for row in fold:
         row_copy = list(row)
         test_set.append(row_copy)
         row_copy[-1] = None
      predicted = algorithm(train_set, test_set, *args)
      actual = [row[-1] for row in fold]
      accuracy = accuracy_metric(actual, predicted)
      scores.append(accuracy)
   return scores
# Splitting a dataset based on an attribute and an attribute value
def test_split(index, value, dataset):
   left, right = list(), list()
   for row in dataset:
      if row[index] < value:
         left.append(row)
      else:
         right.append(row)
   return left, right
# Calculating the Gini index for a split dataset
def gini_index(groups, classes):
   # count all samples at split point
   n_instances = float(sum([len(group) for group in groups]))
   # sum weighted Gini index for each group
   gini = 0.0
   for group in groups:
      size = float(len(group))
      # avoid divide by zero
      if size == 0:
         continue
      score = 0.0
      # score the group based on the score for each class
      for class_val in classes:
         p = [row[-1] for row in group].count(class_val)/size
      score += p * p
      # weight the group score by its relative size
      gini += (1.0 - score) * (size/n_instances)
return gini
# Selecting the best split point for a dataset
def get_split(dataset):
   class_values = list(set(row[-1] for row in dataset))
   b_index, b_value, b_score, b_groups = 999, 999, 999, None
   for index in range(len(dataset[0])-1):
      for row in dataset:
         groups = test_split(index, row[index], dataset)
         gini = gini_index(groups, class_values)
         if gini < b_score:
            b_index, b_value, b_score, b_groups = index, 
row[index], gini, groups
   return {'index':b_index, 'value':b_value, 'groups':b_groups}
# Creating a terminal node value
def to_terminal(group):
outcomes = [row[-1] for row in group]
return max(set(outcomes), key=outcomes.count)
# Creating child splits for a node or make terminal
def split(node, max_depth, min_size, depth):
   left, right = node['groups']
   del(node['groups'])
   # check for a no split
   if not left or not right:
      node['left'] = node['right'] = to_terminal(left + right)
      return
   # check for max depth
   if depth >= max_depth:
      node['left'], node['right'] = to_terminal(left), to_terminal(right)
      return
   # process left child
   if len(left) <= min_size:
      node['left'] = to_terminal(left)
   else:
      node['left'] = get_split(left)
      split(node['left'], max_depth, min_size, depth+1)
   # process right child
   if len(right) <= min_size:
      node['right'] = to_terminal(right)
   else:
      node['right'] = get_split(right)
      split(node['right'], max_depth, min_size, depth+1)
# Building a decision tree
def build_tree(train, max_depth, min_size):
   root = get_split(train)
   split(root, max_depth, min_size, 1)
   return root
# Making a prediction with a decision tree
   def predict(node, row):
   if row[node['index']] < node['value']:
      if isinstance(node['left'], dict):
         return predict(node['left'], row)
      else:
         return node['left']
   else:
      if isinstance(node['right'], dict):
         return predict(node['right'], row)
      else:
         return node['right']
# Classification and Regression Tree Algorithm
def decision_tree(train, test, max_depth, min_size):
   tree = build_tree(train, max_depth, min_size)
   predictions = list()
   for row in test:
      prediction = predict(tree, row)
      predictions.append(prediction)
   return(predictions)
# Testing the Bank Note dataset
seed(1)
# load and prepare data
filename = 'data_banknote_authentication.csv'
dataset = load_csv(filename)
# convert string attributes to integers
for i in range(len(dataset[0])):
   str_column_to_float(dataset, i)
# evaluate algorithm
n_folds = 5
max_depth = 5
min_size = 10
scores = evaluate_algorithm(dataset, decision_tree, n_folds, max_depth, min_size)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))

当您执行上面给出的代码时，您可以按如下方式观察输出 -

Scores: [95.62043795620438, 97.8102189781022, 97.8102189781022, 
94.52554744525547, 98.90510948905109]
Mean Accuracy: 96.934%

Support Vector Machines (SVM)

支持向量机，也称为SVM，是众所周知的监督分类算法，用于分离不同类别的数据。

通过优化线来对这些矢量进行分类，使得每个组中的最近点将彼此最远。

此向量默认为线性，并且通常也可视为线性。 但是，如果内核类型从默认类型“高斯”或线性变化，则矢量也可以采用非线性形式。

它是一种分类方法，其中我们将每个数据项绘制为n维空间中的点（其中n是要素的数量），每个要素的值是特定坐标的值。

例如，如果我们只有两个特征，如个体的Height和Hair length ，我们应该首先在二维空间中绘制这两个变量，其中每个点有两个坐标称为支持向量。 请注意以下图表以便更好地理解 -

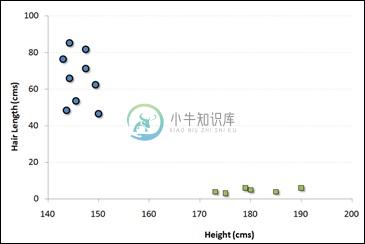
现在，找到一些在两个不同分类的数据组之间分割数据的行。 这将是这样的线，使得距离两组中的每一组中的最近点的距离将最远。

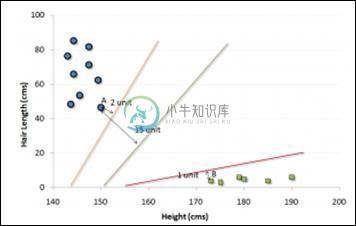
在上面示出的示例中，将数据分成两个不同分类的组的线是黑线，因为两个最接近的点距离线最远。 这一行是我们的分类器。 然后，根据测试数据在线路两侧的位置，我们可以对新数据进行分类。

from sklearn import svm
df = pd.read_csv('iris_df.csv')
df.columns = ['X4', 'X3', 'X1', 'X2', 'Y']
df = df.drop(['X4', 'X3'], 1)
df.head()
from sklearn.cross_validation import train_test_split
support = svm.SVC()
X = df.values[:, 0:2]
Y = df.values[:, 2]
trainX, testX, trainY, testY = train_test_split( X, Y, test_size = 0.3)
sns.set_context('notebook', font_scale=1.1)
sns.set_style('ticks')
sns.lmplot('X1','X2', scatter=True, fit_reg=False, data=df, hue='Y')
plt.ylabel('X2')
plt.xlabel('X1')

运行上面显示的代码时，您会注意到以下输出和绘图 -

Text(0.5,27.256,'X1')

朴素贝叶斯算法

它是一种基于贝叶斯定理的分类技术，假设预测变量是独立的。 简单来说，朴素贝叶斯分类器假定类中特定特征的存在与任何其他特征的存在无关。

例如，如果果实是橙色，圆形，直径约3英寸，则可以认为果实是橙色。 即使这些特征彼此依赖或依赖于其他特征的存在，一个朴素的贝叶斯分类器会认为所有这些特征独立地促成了这种果实是橙色的概率。

朴素贝叶斯模型很容易制作，特别适用于非常大的数据集。 除了简单之外，Naive Bayes的表现甚至超过了先进的分类方法。

贝叶斯定理提供了一种从P（c），P（x）和P（x | c）计算后验概率P（c | x）的方法。 观察这里提供的等式: P(c/x) = P(x/c)P(c)/P(x)

Where,

P（c | x）是给定预测器（属性）的类（目标）的后验概率。

P（c）是先验概率。

P（x | c）是给定类别的预测概率的似然性。

P（x）是预测器的先验概率。

考虑下面给出的示例以便更好地理解 -

假设Weather训练数据集和相应的目标变量Play 。 现在，我们需要根据天气情况对玩家是否玩游戏进行分类。 为此，您必须采取以下步骤 -

Step 1 - 将数据集转换为频率表。

Step 2 - 通过找到阴天概率= 0.29和播放概率为0.64的概率来创建似然表。

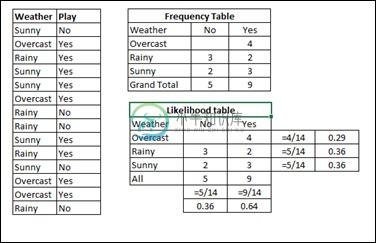
Step 3 - 现在，使用朴素贝叶斯方程计算每个类的后验概率。 具有最高后验概率的类是预测的结果。

Problem - 如果天气晴朗，玩家会玩，这个说法是否正确？

Solution - 我们可以使用上面讨论的方法解决它，所以P（是| Sunny）= P( Sunny | Yes) * P(Yes)/P (Sunny)

我们有，P（晴天|是）= 3/9 = 0.33，P（晴天）= 5/14 = 0.36，P（是）= 9/14 = 0.64

现在，P（是| Sunny）= 0.33 * 0.64/0.36 = 0.60，具有更高的概率。

Naive Bayes使用类似的方法根据各种属性预测不同类别的概率。 该算法主要用于文本分类，并且具有多个类的问题。

以下代码显示了朴素贝叶斯实现的示例 -

import csv
import random
import math
def loadCsv(filename):
   lines = csv.reader(open(filename, "rb"))
   dataset = list(lines)
   for i in range(len(dataset)):
      dataset[i] = [float(x) for x in dataset[i]]
   return dataset
def splitDataset(dataset, splitRatio):
   trainSize = int(len(dataset) * splitRatio)
   trainSet = []
   copy = list(dataset)
   while len(trainSet) < trainSize:
      index = random.randrange(len(copy))
      trainSet.append(copy.pop(index))
   return [trainSet, copy]
def separateByClass(dataset):
   separated = {}
   for i in range(len(dataset)):
      vector = dataset[i]
      if (vector[-1] not in separated):
         separated[vector[-1]] = []
      separated[vector[-1]].append(vector)
return separated
def mean(numbers):
return sum(numbers)/float(len(numbers))
def stdev(numbers):
   avg = mean(numbers)
   variance = sum([pow(x-avg,2) for x in numbers])/float(len(numbers)-1)
   return math.sqrt(variance)
def summarize(dataset):
   summaries = [(mean(attribute), stdev(attribute)) for attribute in zip(*dataset)]
def summarizeByClass(dataset):
   separated = separateByClass(dataset)
   summaries = {}
   for classValue, instances in separated.iteritems():
      summaries[classValue] = summarize(instances)
   return summaries
def calculateProbability(x, mean, stdev):
   exponent = math.exp(-(math.pow(x-mean,2)/(2*math.pow(stdev,2))))
   return (1/(math.sqrt(2*math.pi) * stdev)) * exponent
def calculateClassProbabilities(summaries, inputVector):
   probabilities = {}
   for classValue, classSummaries in summaries.iteritems():
      probabilities[classValue] = 1
      for i in range(len(classSummaries)):
      mean, stdev = classSummaries[i]
      x = inputVector[i]
      probabilities[classValue] *= calculateProbability(x, mean,stdev)
   return probabilities
def predict(summaries, inputVector):
   probabilities = calculateClassProbabilities(summaries, inputVector)
   bestLabel, bestProb = None, -1
   for classValue, probability in probabilities.iteritems():
      if bestLabel is None or probability > bestProb:
         bestProb = probability
         bestLabel = classValue
   return bestLabel
def getPredictions(summaries, testSet):
   predictions = []
   for i in range(len(testSet)):
      result = predict(summaries, testSet[i])
      predictions.append(result)
   return predictions
def getAccuracy(testSet, predictions):
   correct = 0
   for i in range(len(testSet)):
      if testSet[i][-1] == predictions[i]:
         correct += 1
   return (correct/float(len(testSet))) * 100.0
def main():
   filename = 'pima-indians-diabetes.data.csv'
   splitRatio = 0.67
   dataset = loadCsv(filename)
   trainingSet, testSet = splitDataset(dataset, splitRatio)
   print('Split {0} rows into train = {1} and test = {2} rows').format(len(dataset), len(trainingSet), len(testSet))
   # prepare model
   summaries = summarizeByClass(trainingSet)
   # test model
   predictions = getPredictions(summaries, testSet)
   accuracy = getAccuracy(testSet, predictions)
   print('Accuracy: {0}%').format(accuracy)
main()

当您运行上面给出的代码时，您可以观察以下输出 -

Split 1372 rows into train = 919 and test = 453 rows
Accuracy: 83.6644591611%

KNN (K-Nearest Neighbours)

K-Nearest Neighbors，简称KNN，是一种专门用于分类的监督学习算法。 这是一种简单的算法，可以存储所有可用的案例，并通过其k个邻居的多数投票对新案例进行分类。 分配给该类的情况是由距离函数测量的其K个最近邻居中最常见的情况。 这些距离函数可以是欧几里德，曼哈顿，闵可夫斯基和汉明距离。 前三个函数用于连续函数，第四个函数用于分类变量（汉明）。 如果K = 1，则将该情况简单地分配给其最近邻居的类。 有时，在执行KNN建模时，选择K结果是一个挑战。

该算法查看不同的质心并使用某种函数（通常是欧几里得）比较距离，然后分析这些结果并将每个点分配给该组，以便优化它以放置所有最接近的点。

您可以将KNN用于分类和回归问题。 然而，它更广泛地用于工业中的分类问题。 KNN很容易映射到我们的现实生活中。

在选择KNN之前，您必须注意以下几点 -

• KNN在计算上很昂贵。

• 变量应该归一化，否则更高范围的变量会偏向它。

• 在进行KNN之前更多的是在预处理阶段工作，例如异常值，噪声消除

请仔细阅读以下代码以更好地了解KNN -

#Importing Libraries
from sklearn.neighbors import KNeighborsClassifier
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create KNeighbors classifier object model
KNeighborsClassifier(n_neighbors=6) # default value for n_neighbors is 5
# Train the model using the training sets and check score
model.fit(X, y)
#Predict Output
predicted= model.predict(x_test)
from sklearn.neighbors import KNeighborsClassifier
df = pd.read_csv('iris_df.csv')
df.columns = ['X1', 'X2', 'X3', 'X4', 'Y']
df = df.drop(['X4', 'X3'], 1)
df.head()
sns.set_context('notebook', font_scale=1.1)
sns.set_style('ticks')
sns.lmplot('X1','X2', scatter=True, fit_reg=False, data=df, hue='Y')
plt.ylabel('X2')
plt.xlabel('X1')
from sklearn.cross_validation import train_test_split
neighbors = KNeighborsClassifier(n_neighbors=5)
X = df.values[:, 0:2]
Y = df.values[:, 2]
trainX, testX, trainY, testY = train_test_split( X, Y, test_size = 0.3)
neighbors.fit(trainX, trainY)
print('Accuracy: \n', neighbors.score(testX, testY))
pred = neighbors.predict(testX)

上面给出的代码将产生以下输出 -

('Accuracy: \n', 0.75555555555555554)

K-Means

它是一种处理聚类问题的无监督算法。 它的过程遵循一种简单易行的方法，通过一定数量的簇（假设k簇）对给定数据集进行分类。 集群内的数据点是同构的，并且与对等组是异构的。

K-means如何形成集群

K-means在以下步骤中形成集群 -

• K-means为称为质心的每个簇选择k个点。

• 每个数据点形成具有最近质心的簇，即k簇。

• 根据现有集群成员查找每个集群的质心。 在这里，我们有新的质心。

当我们有新的质心时，重复步骤2和3.找到每个数据点与新质心的最近距离，并与新的k-簇相关联。 重复此过程直到收敛发生，直到质心不变。

K的值的确定

在K-means中，我们有集群，每个集群都有自己的质心。 质心与簇内数据点之间的差的平方和构成该簇的平方值之和。 此外，当添加所有聚类的平方值之和时，它在聚类解的平方值之和内变为总和。

我们知道随着聚类数量的增加，这个值会继续下降，但是如果你绘制结果，你可能会看到平方距离之和急剧下降到某个k值，然后慢得多。 在这里，我们可以找到最佳的簇数。

请注意以下代码 -

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.cluster import KMeans
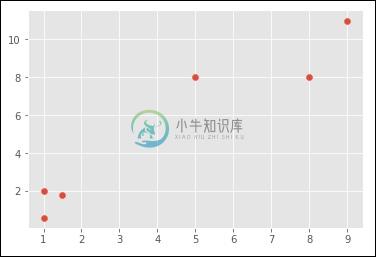
x = [1, 5, 1.5, 8, 1, 9]
y = [2, 8, 1.8, 8, 0.6, 11]
plt.scatter(x,y)
plt.show()
X = np.array([ [1, 2],
               [5, 8],
               [1.5, 1.8],
               [8, 8],
               [1, 0.6],
               [9, 11]])
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
centroids = kmeans.cluster_centers_
labels = kmeans.labels_
print(centroids)
print(labels)
colors = ["g.","r.","c.","y."]
for i in range(len(X)):
   print("coordinate:",X[i], "label:", labels[i])
   plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 10)
plt.scatter(centroids[:, 0],centroids[:, 1], marker = "x", s=150, linewidths = 5, zorder = 10)
plt.show()

当您运行上面给出的代码时，您可以看到以下输出 -

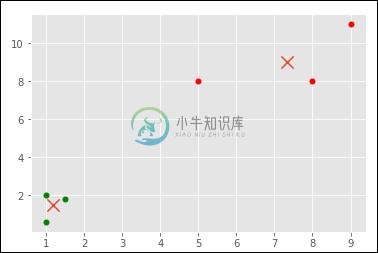
[ [ 1.16666667 1.46666667] [ 7.33333333 9. ] ]
[0 1 0 1 0 1]
('coordinate:', array([ 1., 2.]), 'label:', 0)
('coordinate:', array([ 5., 8.]), 'label:', 1)
('coordinate:', array([ 1.5, 1.8]), 'label:', 0)
('coordinate:', array([ 8., 8.]), 'label:', 1)
('coordinate:', array([ 1. , 0.6]), 'label:', 0)
('coordinate:', array([ 9., 11.]), 'label:', 1)

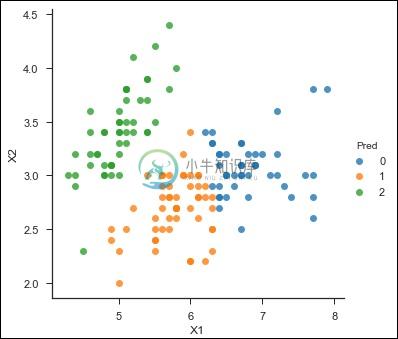
这是您理解的另一个代码 -

from sklearn.cluster import KMeans
df = pd.read_csv('iris_df.csv')
df.columns = ['X1', 'X2', 'X3', 'X4', 'Y']
df = df.drop(['X4', 'X3'], 1)
df.head()
from sklearn.cross_validation import train_test_split
kmeans = KMeans(n_clusters = 3)
X = df.values[:, 0:2]
kmeans.fit(X)
df['Pred'] = kmeans.predict(X)
df.head()
sns.set_context('notebook', font_scale = 1.1)
sns.set_style('ticks')
sns.lmplot('X1','X2', scatter = True, fit_reg = False, data = df, hue = 'Pred')

以下是上述代码的输出 -

<seaborn.axisgrid.FacetGrid at 0x107ad6a0>

随机森林

随机森林是一种流行的监督集成学习算法。 “合奏”意味着它需要一堆“弱学习者”，让他们共同努力，形成一个强有力的预测者。 在这种情况下，弱学习者都是随机实施的决策树，这些决策树汇集在一起​​形成强预测器 - 随机森林。

请注意以下代码 -

from sklearn.ensemble import RandomForestClassifier
df = pd.read_csv('iris_df.csv')
df.columns = ['X1', 'X2', 'X3', 'X4', 'Y']
df.head()
from sklearn.cross_validation import train_test_split
forest = RandomForestClassifier()
X = df.values[:, 0:4]
Y = df.values[:, 4]
trainX, testX, trainY, testY = train_test_split( X, Y, test_size = 0.3)
forest.fit(trainX, trainY)
print('Accuracy: \n', forest.score(testX, testY))
pred = forest.predict(testX)

上面给出的代码的输出是 -

('Accuracy: \n', 1.0)

集合方法的目标是结合使用给定学习算法构建的几个基本估计器的预测，以便改善单个估计器的可普遍性/鲁棒性。

sklearn.ensemble模块包括两个基于随机决策树的平均算法 - the RandomForest algorithm和Extra-Trees method 。 两种算法都是专为树木设计的扰动和组合技术[B1998]。 这意味着通过在分类器构造中引入随机性来创建多种分类器。 集合的预测作为各个分类器的平均预测给出。

森林分类器必须配备两个阵列 - 一个大小为[n_samples，n_features]的稀疏或密集阵列X，用于保存训练样本;一个大小为[n_samples]的阵列Y，用于保存训练样本的目标值（类标签），如下面的代码所示 -

>>> from sklearn.ensemble import RandomForestClassifier
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = RandomForestClassifier(n_estimators = 10)
>>> clf = clf.fit(X, Y)

与决策树一样，树木的森林也会扩展到多输出问题（如果Y是一个大小为[n_samples，n_outputs]的数组）。

与原始出版物[B2001]相反， scikit-learn实现通过平均其概率预测来组合分类器，而不是让每个分类器对单个类别进行投票。

随机森林是决策树集合的商标用语。 在随机森林中，我们有一组决策树，称为“森林”。 为了根据属性对新对象进行分类，每个树都给出一个分类，我们说该树为该类“投票”。 森林选择得票最多的分类（在森林中的所有树木上）。

每棵树的种植和种植如下 -

• 如果训练集中的病例数是N，那么N个病例的样本是随机抽取的，但需要替换。 此示例将是用于种植树的训练集。

• 如果存在M个输入变量，则指定数量m << M，使得在每个节点处，从M中随机选择m个变量，并且使用这些m上的最佳分割来分割节点。 在森林生长期间，m的值保持不变。

• 每棵树都尽可能地生长。 没有修剪。

维数减少算法

维度降低是另一种常见的无监督学习任务。 一些问题可能包含数万甚至数百万的输入或解释变量，这些工作和计算可能代价高昂。 此外，如果某些输入变量捕获噪声或与基础关系无关，则程序的泛化能力可能会降低。

维度减少是查找输出变量的过程，这些变量负责输出或响应变量的最大变化。 降维有时也用于可视化数据。 很容易想象回归问题，例如从其大小预测属性的价格，可以沿着图的x轴绘制属性的大小，并且可以沿y轴绘制属性的价格。 类似地，当添加第二解释变量时，很容易可视化房产价格回归问题。 例如，可以在z轴上绘制房产中的房间数量。 然而，数千个输入变量的问题变得不可能可视化。

降维，将一组非常大的解释变量输入减少到一组较小的输入变量，以保留尽可能多的信息。

PCA是一种降维算法，可以为数据分析做有用的事情。 最重要的是，它可以在处理数百或数千个不同的输入变量时显着减少模型中涉及的计算次数。 由于这是一项无监督的学习任务，用户仍然需要分析结果并确保它们保持原始数据集行为的95％左右。

请注意以下代码以便更好地理解 -

from sklearn import decomposition
df = pd.read_csv('iris_df.csv')
df.columns = ['X1', 'X2', 'X3', 'X4', 'Y']
df.head()
from sklearn import decomposition
pca = decomposition.PCA()
fa = decomposition.FactorAnalysis()
X = df.values[:, 0:4]
Y = df.values[:, 4]
train, test = train_test_split(X,test_size = 0.3)
train_reduced = pca.fit_transform(train)
test_reduced = pca.transform(test)
pca.n_components_

您可以看到上面给出的代码的以下输出 -

4L

在过去的5年中，每个可能的水平和点都有数据捕获量呈指数增长。 政府机构/研究机构/企业不仅提供新的数据来源，而且还在几个点和阶段捕获非常详细的数据。

例如，电子商务公司正在捕获有关客户的更多详细信息，例如他们的人口统计，浏览历史，他们的喜欢或不喜欢，购买历史，反馈和其他一些细节，以给他们定制的关注。 现在可用的数据可能具有数千个功能，并且在保留尽可能多的信息的同时减少这些功能是一项挑战。 在这种情况下，降维有很大帮助。

提升算法

术语“提升”是指将弱学习者转变为强学习者的一系列算法。 让我们通过解决垃圾邮件识别问题来理解这个定义，如下所示 -

将电子邮件分类为垃圾邮件应该遵循什么程序？ 在最初的方法中，我们会使用以下标准识别“垃圾邮件”和“非垃圾邮件”电子邮件，如果 -

• 电子邮件只有一个图像文件（广告图像），它是一个垃圾邮件

• 电子邮件只有链接，这是垃圾邮件

• 电子邮件正文包含“你赢得了$ xxxxxx奖金”之类的句子，这是一个垃圾邮件

• 来自我们官方域名“xnip.cn”的电子邮件，而不是垃圾邮件

• 来自已知来源的电子邮件，而不是垃圾邮件

上面，我们已经定义了几个规则来将电子邮件分类为“垃圾邮件”或“非垃圾邮件”。 但是，这些规则个别不足以成功将电子邮件分类为“垃圾邮件”或“非垃圾邮件”。 因此，这些规则被称为weak learner 。

为了将弱学习者转变为强学习者，我们使用以下方法将每个弱学习者的预测结合起来 -

• 使用平均/加权平均值
• 考虑到投票率较高的预测

例如，假设我们已经定义了7个弱学习者。 在这7个中，有5个被评为“垃圾邮件”，2个投票为“非垃圾邮件”。 在这种情况下，默认情况下，我们会将电子邮件视为垃圾邮件，因为我们对“垃圾邮件”的投票率较高（5）。

它是如何工作的 (How It Works)

提升将弱学习者或基础学习者结合起来形成一个强有力的规则。 本节将向您解释增强功能如何识别弱规则。

为了找到弱规则，我们应用具有不同分布的基础学习（ML）算法。 每次应用基础学习算法时，它都会生成一个新的弱预测规则。 这几次使用迭代过程。 在多次迭代之后，增强算法将这些弱规则组合成单个强预测规则。

要为每轮选择正确的分布，请按照给定的步骤 -

Step 1 - 基础学习者获取所有分布并为每个分配赋予相同的权重。

Step 2 - 如果存在由第一基础学习算法引起的任何预测误差，则我们对具有预测误差的观测值支付更高的权重。 然后，我们应用下一个基础学习算法。

我们迭代步骤2，直到达到基本学习算法的极限或达到更高的精度。

最后，它结合了弱学习者的输出，并形成了一个强大的学习者，最终提高了模型的预测能力。 提升更多地关注由于规则较弱而被错误分类或具有较高错误的示例。

Boosting算法的类型

有几种类型的引擎用于提升算法 - 决策残余，边际最大化分类算法等。 这里列出了不同的增强算法 -

• AdaBoost（自适应提升）
• 渐变树提升
• XGBoost

本节重点介绍AdaBoost和Gradient Boosting，然后是各自的Boosting算法。

AdaBoost

请注意下图解释Ada-boost算法。

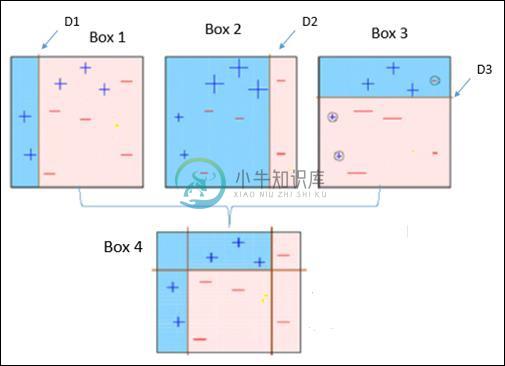
它解释如下 -

Box 1 - 您可以看到我们为每个数据点分配了相同的权重，并应用了决策树桩将它们分类为+（ plus ）或 - （ minus ）。 决策树桩（D1）在左侧创建了一条垂直线来对数据点进行分类。 此垂直线错误地预测三个+（加号）为 - （减号）。 因此，我们将为这三个+（加号）分配更高的权重，并应用另一个决策树桩。

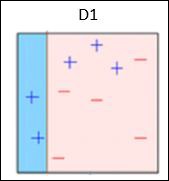
Box 2 - 在这里，可以看出，与其他数据点相比，三个（错误预测的）+（ plus ）数据点的大小更大。 在这种情况下，第二个决策树桩（D2）将尝试正确预测它们。 现在，此框右侧的垂直线（D2）已正确分类三个错误分类+（ plus ）。 但同样，它也犯了错误的分类错误。 这次有三个（ minus ）数据点。 同样，我们将为三个（ minus ）数据点分配更高的权重，并应用另一个决策树桩。

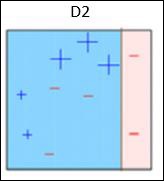
Box 3 - 这里，三（ - minus ）数据点的权重更高。 应用决策残端（D3）来正确预测这些错误分类的观察结果。 这次生成水平线以基于错误分类的观察的较高权重对+（ plus ）和 - （ minus ）数据点进行分类。

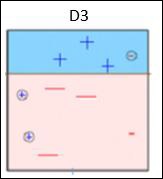
Box 4 - 在这里，我们加入了D1，D2和D3，形成了一个强有力的预测，与单个弱学习者相比，具有复杂的规则。 可以看出，与任何个体弱学习者相比，该算法对这些观察结果进行了很好的分类。

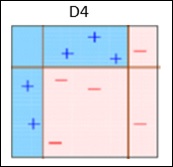
AdaBoost or Adaptive Boosting - 它的工作方式与上面讨论的类似。 它适合不同加权训练数据的弱学习者序列。 它首先预测原始数据集，并给予每次观察相同的权重。 如果使用第一个学习者进行预测不正确，那么它对不正确预测的观察结果给予更高的权重。 作为一个迭代过程，它继续添加学习者，直到达到模型数量或准确度的限制。

大多数情况下，我们使用AdaBoost决策标记。 但是，如果它接受训练数据集的权重，我们可以使用任何机器学习算法作为基础学习器。 我们可以将AdaBoost算法用于分类和回归问题。

您可以使用以下Python代码来实现此目的 -

#for classification
from sklearn.ensemble import AdaBoostClassifier
#for regression
from sklearn.ensemble import AdaBoostRegressor
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier()
clf = AdaBoostClassifier(n_estimators=100, base_estimator=dt,learning_rate=1)
#Here we have used decision tree as a base estimator; Any ML learner can be used as base #estimator if it accepts sample weight
clf.fit(x_train,y_train)

调整参数

可以调整参数以优化算法的性能。调整的关键参数是 -

n_estimators - 它们控制弱学习者的数量。

learning_rate - 它控制弱学习者在最终组合中的贡献。 在learning_rate和n_estimators之间进行权衡。

base_estimators - 这些有助于指定不同的ML算法。

还可以调整基础学习者的参数以优化其性能。

渐变提升

在梯度增强中，许多模型被顺序训练。 每个新模型使用梯度下降法逐渐最小化整个系统的损失函数（y = ax + b + e，其中'e'是误差项）。 学习方法连续适合新模型，以更准确地估计响应变量。

该算法背后的主要思想是构建新的基础学习器，其可以与损失函数的负梯度最佳地相关，与整个集合相关。

在Python Sklearn库中，我们使用Gradient Tree Boosting或GBRT，这是对任意可微分损失函数的推广的推广。 它可以用于回归和分类问题。

您可以使用以下代码来实现此目的 -

#for classification
from sklearn.ensemble import GradientBoostingClassifier
#for regression
from sklearn.ensemble import GradientBoostingRegressor
clf = GradientBoostingClassifier(n_estimators = 100, learning_rate = 1.0, max_depth = 1)
clf.fit(X_train, y_train)

以下是上述代码中使用的术语 -

n_estimators - 它们控制弱学习者的数量。

learning_rate - 它控制弱学习者在最终组合中的贡献。 在learning_rate和n_estimators之间进行权衡。

max_depth - 这是限制树中节点数的各个回归估计器的最大深度。 调整此参数以获得最佳性能，最佳值取决于输入变量的交互。

可以调整损耗函数以获得更好的性能。