Neural Networks
神经网络是并行计算设备,其试图建立大脑的计算机模型。 其背后的主要目标是开发一个系统,以比传统系统更快地执行各种计算任务。 这些任务包括模式识别和分类,近似,优化和数据聚类。
什么是人工神经网络(ANN)
人工神经网络(ANN)是一种高效的计算系统,其中心主题借鉴了生物神经网络的类比。 人工神经网络也被称为人工神经系统,并行分布式处理系统和连接系统。 ANN收集了大量的单元,这些单元以某种模式互连,以便在它们之间进行通信。 这些单元,也称为nodes或neurons ,是并行操作的简单处理器。
每个神经元通过connection link与其他神经元connection link 。 每个连接链路与具有关于输入信号的信息的权重相关联。 这是神经元解决特定问题的最有用信息,因为weight通常会激发或抑制正在传递的信号。 每个神经元都具有其内部状态,称为activation signal 。 在组合输入信号和激活规则之后产生的输出信号可以被发送到其他单元。
如果您想详细研究神经网络,那么您可以按照链接 - Artificial Neural Network 。
安装有用的包
为了在Python中创建神经网络,我们可以使用一个名为NeuroLab神经网络的强大包。 它是一个基本的神经网络算法库,具有灵活的网络配置和Python学习算法。 您可以在命令提示符下使用以下命令安装此软件包 -
pip install NeuroLab
如果您使用的是Anaconda环境,请使用以下命令安装NeuroLab -
conda install -c labfabulous neurolab
构建神经网络
在本节中,让我们使用NeuroLab包在Python中构建一些神经网络。
基于感知器的分类器
感知器是人工神经网络的基石。 如果您想了解更多关于Perceptron的信息,可以点击链接 - artificial_neural_network
以下是逐步执行Python代码,用于构建基于简单神经网络感知器的分类器 -
如图所示导入必要的包 -
import matplotlib.pyplot as plt
import neurolab as nl
输入输入值。 请注意,这是监督学习的一个例子,因此您也必须提供目标值。
input = [[0, 0], [0, 1], [1, 0], [1, 1]]
target = [[0], [0], [0], [1]]
使用2个输入和1个神经元创建网络 -
net = nl.net.newp([[0, 1],[0, 1]], 1)
现在,训练网络。 在这里,我们使用Delta规则进行培训。
error_progress = net.train(input, target, epochs=100, show=10, lr=0.1)
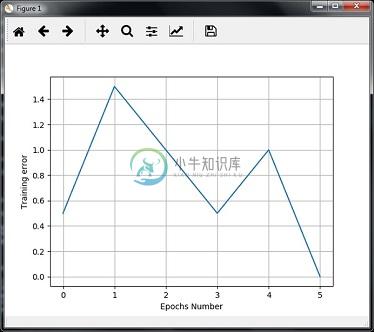
现在,可视化输出并绘制图形 -
plt.figure()
plt.plot(error_progress)
plt.xlabel('Number of epochs')
plt.ylabel('Training error')
plt.grid()
plt.show()
您可以使用错误指标查看以下显示培训进度的图表 -
单层神经网络
在这个例子中,我们创建了一个单层神经网络,它由作用于输入数据的独立神经元组成,以产生输出。 请注意,我们使用名为neural_simple.txt的文本文件作为输入。
导入有用的包如图所示 -
import numpy as np
import matplotlib.pyplot as plt
import neurolab as nl
加载数据集如下 -
input_data = np.loadtxt(“/Users/admin/neural_simple.txt')
以下是我们将要使用的数据。 请注意,在此数据中,前两列是要素,后两列是标签。
array([[2. , 4. , 0. , 0. ],
[1.5, 3.9, 0. , 0. ],
[2.2, 4.1, 0. , 0. ],
[1.9, 4.7, 0. , 0. ],
[5.4, 2.2, 0. , 1. ],
[4.3, 7.1, 0. , 1. ],
[5.8, 4.9, 0. , 1. ],
[6.5, 3.2, 0. , 1. ],
[3. , 2. , 1. , 0. ],
[2.5, 0.5, 1. , 0. ],
[3.5, 2.1, 1. , 0. ],
[2.9, 0.3, 1. , 0. ],
[6.5, 8.3, 1. , 1. ],
[3.2, 6.2, 1. , 1. ],
[4.9, 7.8, 1. , 1. ],
[2.1, 4.8, 1. , 1. ]])
现在,将这四列分成2个数据列和2个标签 -
data = input_data[:, 0:2]
labels = input_data[:, 2:]
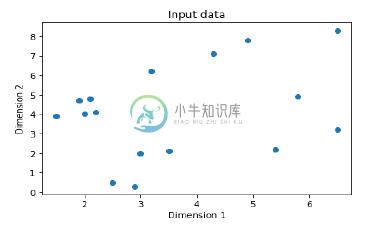
使用以下命令绘制输入数据 -
plt.figure()
plt.scatter(data[:,0], data[:,1])
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.title('Input data')
现在,定义每个维度的最小值和最大值,如下所示 -
dim1_min, dim1_max = data[:,0].min(), data[:,0].max()
dim2_min, dim2_max = data[:,1].min(), data[:,1].max()
接下来,定义输出层中的神经元数量,如下所示 -
nn_output_layer = labels.shape[1]
现在,定义一个单层神经网络 -
dim1 = [dim1_min, dim1_max]
dim2 = [dim2_min, dim2_max]
neural_net = nl.net.newp([dim1, dim2], nn_output_layer)
如图所示,训练具有历元数和学习率的神经网络 -
error = neural_net.train(data, labels, epochs = 200, show = 20, lr = 0.01)
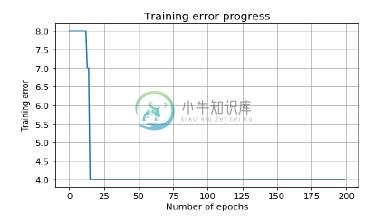
现在,使用以下命令可视化并绘制训练进度 -
plt.figure()
plt.plot(error)
plt.xlabel('Number of epochs')
plt.ylabel('Training error')
plt.title('Training error progress')
plt.grid()
plt.show()
现在,使用上面分类器中的测试数据点 -
print('\nTest Results:')
data_test = [[1.5, 3.2], [3.6, 1.7], [3.6, 5.7],[1.6, 3.9]] for item in data_test:
print(item, '-->', neural_net.sim([item])[0])
您可以在此处找到测试结果 -
[1.5, 3.2] --> [1. 0.]
[3.6, 1.7] --> [1. 0.]
[3.6, 5.7] --> [1. 1.]
[1.6, 3.9] --> [1. 0.]
您可以看到以下图表作为到目前为止讨论的代码的输出 -
多层神经网络
在这个例子中,我们创建了一个多层神经网络,它由多个层组成,以提取训练数据中的底层模式。 这种多层神经网络将像回归器一样工作。 我们将基于以下等式生成一些数据点:y = 2x 2 +8。
如图所示导入必要的包 -
import numpy as np
import matplotlib.pyplot as plt
import neurolab as nl
基于上述等式生成一些数据点 -
min_val = -30
max_val = 30
num_points = 160
x = np.linspace(min_val, max_val, num_points)
y = 2 * np.square(x) + 8
y /= np.linalg.norm(y)
现在,重塑此数据集如下 -
data = x.reshape(num_points, 1)
labels = y.reshape(num_points, 1)
使用以下命令可视化和绘制输入数据集 -
plt.figure()
plt.scatter(data, labels)
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
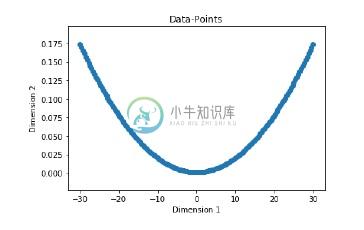
plt.title('Data-points')
现在,构建具有两个隐藏层的神经网络,其中神经元在第一个隐藏层中具有ten神经元,在第二个隐藏层中具有six神经元,在输出层中具有一个神经元。
neural_net = nl.net.newff([[min_val, max_val]], [10, 6, 1])
现在使用渐变训练算法 -
neural_net.trainf = nl.train.train_gd
现在训练网络的目的是学习上面生成的数据 -
error = neural_net.train(data, labels, epochs = 1000, show = 100, goal = 0.01)
现在,在训练数据点上运行神经网络 -
output = neural_net.sim(data)
y_pred = output.reshape(num_points)
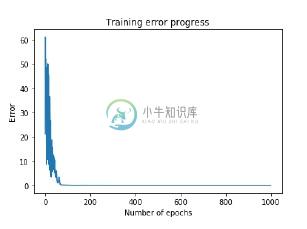
现在绘图和可视化任务 -
plt.figure()
plt.plot(error)
plt.xlabel('Number of epochs')
plt.ylabel('Error')
plt.title('Training error progress')
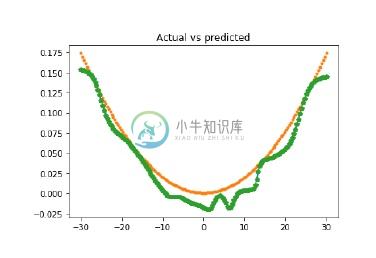
现在我们将绘制实际与预测的输出 -
x_dense = np.linspace(min_val, max_val, num_points * 2)
y_dense_pred = neural_net.sim(x_dense.reshape(x_dense.size,1)).reshape(x_dense.size)
plt.figure()
plt.plot(x_dense, y_dense_pred, '-', x, y, '.', x, y_pred, 'p')
plt.title('Actual vs predicted')
plt.show()
作为上述命令的结果,您可以观察如下所示的图形 -