分析时间序列数据（Analyzing Time Series Data）

优质

小牛编辑

123浏览

2023-12-01

预测给定输入序列中的下一个是机器学习中的另一个重要概念。本章为您提供有关分析时间序列数据的详细说明。

介绍 (Introduction)

时间序列数据表示一系列特定时间间隔内的数据。如果我们想在机器学习中构建序列预测，那么我们必须处理顺序数据和时间。系列数据是顺序数据的摘要。数据排序是顺序数据的重要特征。

序列分析或时间序列分析的基本概念

序列分析或时间序列分析是基于先前观察到的预测给定输入序列中的下一个。预测可以是接下来可能出现的任何事情:符号，数字，次日天气，下一个语音等。序列分析在诸如股票市场分析，天气预报和产品推荐等应用中非常方便。

Example

请考虑以下示例以了解序列预测。这里A,B,C,D是给定值，您必须使用序列预测模型预测值E

安装有用的包

对于使用Python的时间序列数据分析，我们需要安装以下包 -

Pandas

Pandas是一个开源的BSD许可库，为Python提供高性能，易于使用的数据结构和数据分析工具。您可以借助以下命令安装Pandas -

pip install pandas

如果您正在使用Anaconda并希望使用conda软件包管理器进行安装，那么您可以使用以下命令 -

conda install -c anaconda pandas

hmmlearn

它是一个开源的BSD许可库，由简单的算法和模型组成，用于学习Python中的隐马尔可夫模型（HMM）。您可以借助以下命令安装它 -

pip install hmmlearn

如果您正在使用Anaconda并希望使用conda软件包管理器进行安装，那么您可以使用以下命令 -

conda install -c omnia hmmlearn

PyStruct

它是一个结构化的学习和预测库。在PyStruct中实现的学习算法具有诸如条件随机场（CRF），最大边缘马尔可夫随机网络（M3N）或结构支持向量机之类的名称。您可以借助以下命令安装它 -

pip install pystruct

CVXOPT

它用于基于Python编程语言的凸优化。它也是一个免费的软件包。您可以在以下命令的帮助下安装它 -

pip install cvxopt

如果您正在使用Anaconda并希望使用conda软件包管理器进行安装，那么您可以使用以下命令 -

conda install -c anaconda cvdoxt

熊猫:从时间序列数据处理，切片和提取统计数据

如果您必须处理时间序列数据，Pandas是一个非常有用的工具。在Pandas的帮助下，您可以执行以下操作 -

使用pd.date_range包创建一系列日期
使用pd.Series包索引带有日期的pd.Series
使用ts.resample包执行重新采样
改变频率

例子 (Example)

以下示例显示使用Pandas处理和切片时间序列数据。请注意，这里我们使用的是每月北极涛动数据，可以从monthly.ao.index.b50.current.ascii下载，并可以转换为文本格式供我们使用。

处理时间序列数据

要处理时间序列数据，您必须执行以下步骤 -

第一步涉及导入以下包 -

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

接下来，定义一个函数，它将从输入文件中读取数据，如下面给出的代码所示 -

def read_data(input_file):
   input_data = np.loadtxt(input_file, delimiter = None)

现在，将此数据转换为时间序列。为此，请创建时间序列的日期范围。在这个例子中，我们保留一个月的数据频率。我们的文件的数据从1950年1月开始。

dates = pd.date_range('1950-01', periods = input_data.shape[0], freq = 'M')

在此步骤中，我们在Pandas系列的帮助下创建时间序列数据，如下所示 -

output = pd.Series(input_data[:, index], index = dates)	
return output
if __name__=='__main__':

输入输入文件的路径，如下所示 -

input_file = "/Users/admin/AO.txt"

现在，将列转换为timeseries格式，如下所示 -

timeseries = read_data(input_file)

最后，使用显示的命令绘制并可视化数据 -

plt.figure()
timeseries.plot()
plt.show()

您将观察到如下图所示的图 -

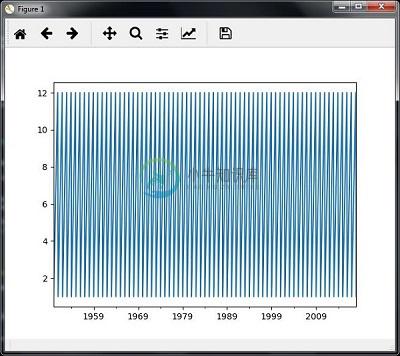
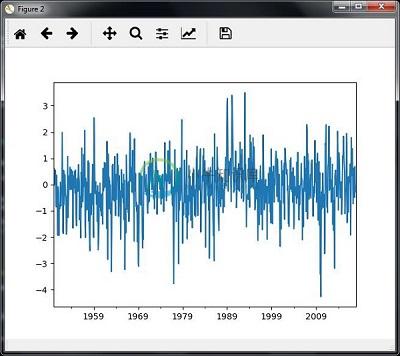
切片时间序列数据

切片涉及仅检索时间序列数据的某些部分。作为示例的一部分，我们仅从1980年到1990年对数据进行切片。观察以下执行此任务的代码 -

timeseries['1980':'1990'].plot()
   <matplotlib.axes._subplots.AxesSubplot at 0xa0e4b00>
plt.show()

当您运行用于切片时间序列数据的代码时，您可以观察到如下图所示 - 如下图所示 -

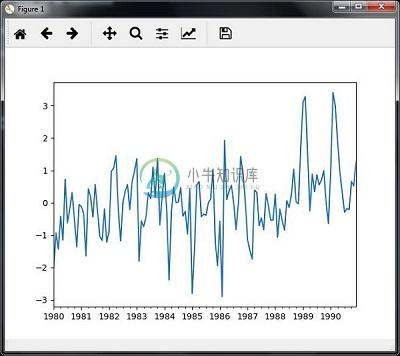
从时间序列数据中提取统计量

在需要得出一些重要结论的情况下，您必须从给定数据中提取一些统计数据。平均值，方差，相关性，最大值和最小值是一些此类统计数据。如果要从给定的时间序列数据中提取此类统计信息，可以使用以下代码 -

Mean

您可以使用mean()函数来查找均值，如下所示 -

timeseries.mean()

然后，您将针对所讨论的示例观察到的输出是 -

-0.11143128165238671

Maximum

您可以使用max()函数来查找最大值，如下所示 -

timeseries.max()

然后，您将针对所讨论的示例观察到的输出是 -

3.4952999999999999

Minimum

您可以使用min（）函数来查找最小值，如下所示 -

timeseries.min()

然后，您将针对所讨论的示例观察到的输出是 -

-4.2656999999999998

一劳永逸

如果要一次计算所有统计信息，可以使用describe()函数，如下所示 -

timeseries.describe()

然后，您将针对所讨论的示例观察到的输出是 -

count   817.000000
mean     -0.111431
std       1.003151
min      -4.265700
25%      -0.649430
50%      -0.042744
75%       0.475720
max       3.495300
dtype: float64

重新取样

您可以将数据重新采样到不同的时间频率。进行重新采样的两个参数是 -

Time period
Method

Re-sampling with mean()

您可以使用以下代码使用mean（）方法重新采样数据，这是默认方法 -

timeseries_mm = timeseries.resample("A").mean()
timeseries_mm.plot(style = 'g--')
plt.show()

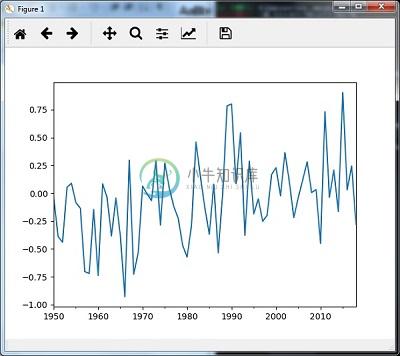
然后，您可以使用mean（）观察以下图表作为重采样的输出 -

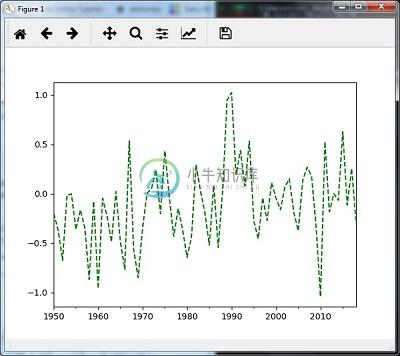
Re-sampling with median()

您可以使用以下代码使用median（）方法重新采样数据 -

timeseries_mm = timeseries.resample("A").median()
timeseries_mm.plot()
plt.show()

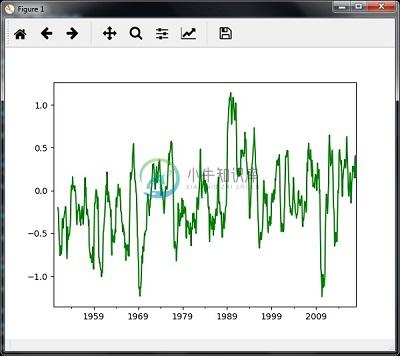
然后，您可以观察下图作为中位数（）重新采样的输出 -

滚动平均值

您可以使用以下代码计算滚动（移动）平均值 -

timeseries.rolling(window = 12, center = False).mean().plot(style = '-g')
plt.show()

然后，您可以观察下图作为滚动（移动）平均值的输出 -

用隐马尔可夫模型（HMM）分析序列数据

HMM是一种统计模型，广泛用于具有延续性和可扩展性的数据，如时间序列股票市场分析，健康检查和语音识别。本节详细介绍了使用隐马尔可夫模型（HMM）分析顺序数据。

Hidden Markov Model (HMM)

HMM是一个随机模型，它基于马尔可夫链的概念，基于以下假设:未来统计数据的概率仅取决于当前的过程状态而不是之前的任何状态。例如，当投掷硬币时，我们不能说第五次投掷的结果将是一个头。这是因为硬币没有任何记忆，下一个结果不依赖于之前的结果。

在数学上，HMM由以下变量组成 -

States (S)

它是HMM中存在的一组隐藏或潜在状态。它由S.表示

Output symbols (O)

它是HMM中存在的一组可能的输出符号。它用O表示。

状态转移概率矩阵（A）

它是从一个状态转换到每个其他状态的概率。它用A表示。

观测发射概率矩阵（B）

它是在特定状态下发射/观察符号的概率。它由B表示。

Prior Probability Matrix (Π)

它是从系统的各种状态开始于特定状态的概率。它用Π表示。

因此，HMM可以定义为???? = (S,O,A,B,????) ???? = (S,O,A,B,????) ，

Where,

S = {s ₁ ,s ₂ ,…,s _N }是N个可能状态的集合，
O = {o ₁ ,o ₂ ,…,o _M }是一组M个可能的观察符号，
A是N????N状态转移概率矩阵（TPM），
B是N????M观测或发射概率矩阵（EPM），
π是N维初始状态概率分布矢量。

示例:股市数据分析

在这个例子中，我们将逐步分析股票市场的数据，以了解HMM如何与顺序或时间序列数据一起工作。请注意，我们正在Python中实现此示例。

导入必要的包，如下所示 -

import datetime
import warnings

现在，使用matpotlib.finance包中的股票市场数据，如下所示 -

import numpy as np
from matplotlib import cm, pyplot as plt
from matplotlib.dates import YearLocator, MonthLocator
try:
   from matplotlib.finance import quotes_historical_yahoo_och1
except ImportError:
   from matplotlib.finance import (
      quotes_historical_yahoo as quotes_historical_yahoo_och1)
from hmmlearn.hmm import GaussianHMM

从开始日期和结束日期加载数据，即在此处显示的两个特定日期之间加载数据 -

start_date = datetime.date(1995, 10, 10)
end_date = datetime.date(2015, 4, 25)
quotes = quotes_historical_yahoo_och1('INTC', start_date, end_date)

在此步骤中，我们将每天提取结束引号。为此，请使用以下命令 -

closing_quotes = np.array([quote[2] for quote in quotes])

现在，我们将提取每天交易的股票数量。为此，请使用以下命令 -

volumes = np.array([quote[5] for quote in quotes])[1:]

在这里，使用下面显示的代码获取收盘价格的百分比差异 -

diff_percentages = 100.0 * np.diff(closing_quotes)/closing_quotes[:-]
dates = np.array([quote[0] for quote in quotes], dtype = np.int)[1:]
training_data = np.column_stack([diff_percentages, volumes])

在此步骤中，创建并训练高斯HMM。为此，请使用以下代码 -

hmm = GaussianHMM(n_components = 7, covariance_type = 'diag', n_iter = 1000)
with warnings.catch_warnings():
   warnings.simplefilter('ignore')
   hmm.fit(training_data)

现在，使用HMM模型生成数据，使用显示的命令 -

num_samples = 300
samples, _ = hmm.sample(num_samples)

最后，在此步骤中，我们绘制并可视化以图表形式作为输出交易的股票的差异百分比和数量。

使用以下代码绘制和可视化差异百分比 -

plt.figure()
plt.title('Difference percentages')
plt.plot(np.arange(num_samples), samples[:, 0], c = 'black')

使用以下代码绘制和可视化交易的股票数量 -

plt.figure()
plt.title('Volume of shares')
plt.plot(np.arange(num_samples), samples[:, 1], c = 'black')
plt.ylim(ymin = 0)
plt.show()