10.5.1 算法复杂度

优质

小牛编辑

131浏览

2023-12-01

10.5.1 算法复杂度

为了回答上述问题，首先要明确如何衡量算法的好坏。以搜索问题为例，线性搜索算法

直接了当，易设计易实现，这算不算“好”？而二分搜索算法虽然设计实现稍难一些，但因无需检查每一个数据而大大提高了搜索效率，这又算不算“好”？

在解决数学问题时，不论是证明定理还是计算表达式，只要证明过程正确、计算结果精确，问题就可以认为成功地解决了，即正确性、精确性是评价数学解法好坏的标准。而在用计算机解决问题时，仅仅要求算法能正确、精确地解决问题，是不够的。试想，假如一个算法虽然能够正确地解决问题，但需要在计算机上运行 100 年或者需要占用 100TB 的内存，这样的算法有实际意义吗？不要以为 100 年或 100TB 是危言耸听，很多简单算法都可能轻易地达到或突破这样的需求（参见稍后对 Hanoi 塔算法的分析）。可见，利用计算机解决问题必须考虑算法的经济性，即算法所耗费的资源问题。计算机用户当然都希望能多快好省地解决问题，因此好的算法应当尽量少地耗费资源。

通常只考虑算法所占用的 CPU 时间和存储器空间这两种资源①。所谓算法分析，就是分析特定算法在运行时所耗费的时间和存储空间的数量，分别称为算法的时间复杂度和空间复杂度。本节只讨论算法的时间复杂度，毕竟存储空间的大小在现代计算机中已经越来越不再是一个问题。

虽然讨论的是算法耗费的“时间”，但我们并不是真的去测量程序在计算机中的实际运行时间，因为实际运行时间依赖于特定机器平台（CPU、内存、操作系统、编程语言等），同一算法在不同平台上执行可能得到不同的分析结果，故很难据此对算法进行分析和比较。例如，在最先进的计算机上执行线性搜索也许比在老式计算机上执行二分搜索要快，据此得出线性搜索优于二分搜索显然不合理。

实际上，算法分析指的是分析算法的代码，估计出为解决问题需要执行的操作（或语句、指令等类似概念）的数目，或称算法的“步数”。之所以分析算法步数，是因为：第一，步数确实能反映执行时间——步数越多执行时间就越长；第二，算法的步数不依赖于平台，更容易分析和比较。

例如，下面的函数 f1()需要执行 11 次赋值操作，其中包含 10 次加法运算②：

def f1():
    x = 0
    for i in range(10): 
        x = x + 1

而下面的函数 f2()需要 21 次赋值操作（20 次加法）：

def f2():
    x = 0
    for i in range(20): 
        x = x + 1

比较一下 f1 和 f2，显然 f1 运行时间更短，但这并不意味着 f1 比 f2 采用的算法“好”，因为它们的“算法”显然是一样的，只不过 f1 要处理的数据更少：f1 将 10 个 1 相加，而 f2 将 20 个 1 相加。可见，算法复杂度是跟算法处理的数据量有关的。

算法通常都设计成能处理任意大小的输入数据，这就导致算法的步数并不是固定的，而是随着问题规模的变化而变化，因此算法的步数可表示为问题规模的函数。假设用 n 表示问题规模，算法分析不仅要考虑算法步数与 n 的关系，更重要的是还要考虑“当 n 逐渐增大时” 算法复杂度会如何变化。例如，将上述 f1 和 f2 改写成更一般的形式：

① 不考虑开发算法的人力物力等代价。
② 注意我们分析的层次是源代码级别，而不是机器指令级别。

def f(n):
    x = 0
    for i in range(n): 
        x = x + 1

不难得出此函数需要执行的步数为 n+1。当 n 增大时，算法执行时间也会增加，而且是线性地增加，即：当 n 增加 1 倍变成 2n，执行时间变成 2n+1，大约比 n+1 增加 1 倍。

说 A 算法比 B 算法好，并不是指对于特定的 n，A 比 B 节省 50%的时间，而是指随着 n 的不断增大，A 对 B 的优势会越来越大。

算法复杂度的大 O 表示法

再次观察上面例子中函数 f()的步数表达式“n+1”，不难看出其中对执行时间起决定作用的是 n，而 n 后面的+1 是可以忽略不计的。按照“当 n 逐渐增大时”进行分析的思想，即便是 n+100、n+1000000 中，n 后面的常数也是可以忽略不计的，因为与逐渐增大趋于∞ 的 n 相比，任何常数都是浮云。事实上，分析算法复杂度时，我们只分析其增长的数量级，而不是分析其精确的步数公式。

数学中的“大 O 表示法”根据函数的增长率特性来刻画函数，可以用来描述算法的复杂度。令 f(n)和 g(n)是两个函数，如果存在正常数 c，使得只要 n 足够大（例如超过某个 n0），函数 f(n)的值都不会超过 c×g(n)，即当 n > n0 时，

f(n) <= c x g(n)

则可记为

f (n) = O(g(n))

在描述算法复杂度时，n 对应于问题规模，f(n)是算法需执行的步数，g(n)是表示增长数量级的某个函数。说算法的复杂度为 O(g(n))，意思就是当 n 足够大时，该算法的执行步数（时间）永远不会超过 c×g(n)。

例如，假设一个算法当输入规模为 n 时需要执行 n+100 条指令，则当 n 足够大时（只要大于 100），

n + 100 <= n + n = 2n

套用大 O 表示法的定义，取 g(n)=n，则可将此算法的复杂度表示为 O(n)。同理，如果一个算法的步数为 n+1000000，它的复杂度仍然可表示为 O(n)。由此可见，两个不同的算法虽然具有不同的代码和执行步数，但完全可能具有相同的复杂度，即当问题规模足够大时，它们的执行时间按相同数量级的增长率增长，利用大 O 表示法即可描述这一点。

实际分析算法时，为了使 O(g(n))中的 g(n)函数尽量简单，在得到算法的步数表达式 f(n) 之后，可以利用两条规则来简化推导，直接得出 f(n)的大 O 表示。规则如下：

（1）如果 f(n)是若干项之和，则只需保留最高次项，省略所有低次项；

（2）如果 f(n)是若干项之积，则可省略任何常数因子（即与 n 无关的因子）。例如，分析下列代码：

def f(n):
    x = 0
    for i in range(n): 
        for j in range(n):
            for k in range(n): 
                x = x + 1
    for i in range(n): 
        for j in range(n):
            for k in range(n): 
                x = x + 1
    for i in range(n): 
        x = x + 1

易知此算法的步数为 2n³+n+1。根据第一条规则，可只保留 2n3；再根据第二条规则，可只保留 n³。所以，此算法的复杂度为 O(n³)。当然我们也可以直接从 f(n)开始推导，利用大 O表示法的定义来验证这个结果是正确的：对于 n > 1，

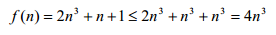
取 g(n)为 n3，c 为 4，即得 f(n) = O(n3)。总之，以上两条规则告诉我们，在分析算法代码时可以忽略许多代码，而只关注那些嵌套层数最多、并且每一层循环的循环次数都与问题规模 n 有关的循环。