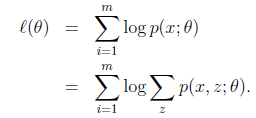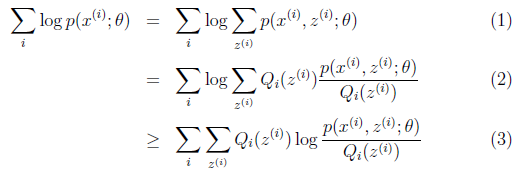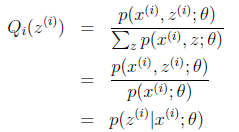EM 最大期望算法
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html 我的数据挖掘算法代码实现: https://github.com/linyiqun/DataMiningAlgorithm
介绍
em算法是一种迭代算法,用于含有隐变量的参数模型的最大似然估计或极大后验概率估计。EM算法,作为一个框架思想,它可以应用在很多领域,比如说数据聚类领域----模糊聚类的处理,待会儿也会给出一个这样的实现例子。
EM算法原理
EM算法从名称上就能看出他可以被分成2个部分,E-Step和M-Step。E-Step叫做期望化步骤,M-Step为最大化步骤。
整体算法的步骤如下所示:
1、初始化分布参数。
2、(E-Step)计算期望E,利用对隐藏变量的现有估计值,计算其最大似然估计值,以此实现期望化的过程。
3、(M-Step)最大化在E-步骤上的最大似然估计值来计算参数的值
4、重复2,3步骤直到收敛。
以上就是EM算法的核心原理,也许您会想,真的这么简单,其实事实是我省略了其中复杂的数据推导的过程,因为如果不理解EM的算法原理,去看其中的数据公式的推导,会让人更加晕的。好,下面给出数据的推导过程,本人数学也不好,于是用了别人的推导过程,人家已经写得非常详细了。
EM算法的推导过程
jensen不等式
在介绍推导过程的时候,需要明白jensen不等式,他是一个关于凸函数的一个定理,直接上公式定义;
如果f是凸函数,X是随机变量,那么
特别地,如果f是严格凸函数,那么![]() 当且仅当
当且仅当![]() ,也就是说X是常量。
,也就是说X是常量。
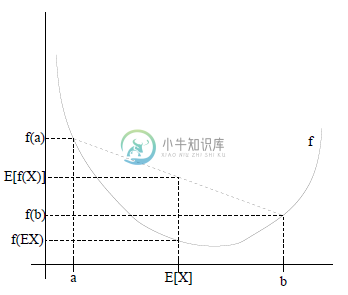
如果用图表示会很清晰:
这里需要解释的是E(X)的值为什么是(a+b)/2,因为有0.5 的概率是a,0.5的概率是b,于是他的期望就是a,b的和的中间值了。同理在y轴上的值也是如此。EM算法的公式表达形式
EM算法转化为公式的表达形式为:
给定的训练样本是![]() ,样例间独立,我们想找到每个样例隐含的类别z,能使得p(x,z)最大。p(x,z)的最大似然估计如下:
,样例间独立,我们想找到每个样例隐含的类别z,能使得p(x,z)最大。p(x,z)的最大似然估计如下:
可以由前面阐述的内容得到下面的公式:
(1)到(2)比较直接,就是分子分母同乘以一个相等的函数。(2)到(3)利用了Jensen不等式。对于每一个样例i,让![]() 表示该样例隐含变量z的某种分布,
表示该样例隐含变量z的某种分布,![]() 满足的条件是
满足的条件是![]() 。于是就来到了问题的关键,通过上面的不等式,我们就可以确定式子的下界,然后我们就可以不断的提高此下界达到逼近最后真实值的目的值,那么什么时候达到想到的时候呢,没错,就是这个不等式变成等式的时候,然后再依据之前描述的jensen不等式的说明,当不等式变为等式的时候,
。于是就来到了问题的关键,通过上面的不等式,我们就可以确定式子的下界,然后我们就可以不断的提高此下界达到逼近最后真实值的目的值,那么什么时候达到想到的时候呢,没错,就是这个不等式变成等式的时候,然后再依据之前描述的jensen不等式的说明,当不等式变为等式的时候,![]() 当且仅当
当且仅当![]() ,也就是说X是常量,推出就是下面的公式:
,也就是说X是常量,推出就是下面的公式:
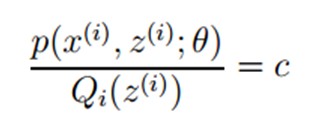
再推导下,由于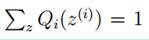 (因为Q是随机变量z(i)的概率密度函数),则可以得到:分子的和等于c(分子分母都对所有z(i)求和:多个等式分子分母相加不变,这个认为每个样例的两个概率比值都是c),再次继续推导;
(因为Q是随机变量z(i)的概率密度函数),则可以得到:分子的和等于c(分子分母都对所有z(i)求和:多个等式分子分母相加不变,这个认为每个样例的两个概率比值都是c),再次继续推导;
循环重复直到收敛
(E步)对于每一个i,计算
(M步)计算
也许你看完这个数学推导的过程已经开始头昏了,没有关系,下面给出一个实例,让大家真切的感受一下EM算法的神奇。EM算法的模糊聚类实现
在这里我会给出一个自己实现的基于EM算法的计算模糊聚类。
输入测试的数据文件,里面包含了a-f 7个点坐标:
3 3 4 10 9 6 14 8 18 11 21 7开始时默认簇中心点C1, C2为a和b。这就算是参数的初始赋值,然后是主要的操作;
1、E-Step:期望步根据当前的的模糊聚类或概率簇的参数,把对象指派到簇中。
2、M-Step:最大化步发现新的聚类或参数,最小化模糊聚类的SSE(对象的误差平方和,这个在程序中会有所体现)。在M步中会用到这个公式,根据划分矩阵重新调整计算簇的中心。
最后的收敛条件为,计算出的簇中心点的坐标的横纵坐标轴的误差和不超过1.0,意味着基本不再变化了。
主程序类:
package DataMining_EM;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.text.MessageFormat;
import java.util.ArrayList;
/**
* EM最大期望算法工具类
*
* @author lyq
*
*/
public class EMTool {
// 测试数据文件地址
private String dataFilePath;
// 测试坐标点数据
private String[][] data;
// 测试坐标点数据列表
private ArrayList<Point> pointArray;
// 目标C1点
private Point p1;
// 目标C2点
private Point p2;
public EMTool(String dataFilePath) {
this.dataFilePath = dataFilePath;
pointArray = new ArrayList<>();
}
/**
* 从文件中读取数据
*/
public void readDataFile() {
File file = new File(dataFilePath);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
data = new String[dataArray.size()][];
dataArray.toArray(data);
// 开始时默认取头2个点作为2个簇中心
p1 = new Point(Integer.parseInt(data[0][0]),
Integer.parseInt(data[0][1]));
p2 = new Point(Integer.parseInt(data[1][0]),
Integer.parseInt(data[1][1]));
Point p;
for (String[] array : data) {
// 将数据转换为对象加入列表方便计算
p = new Point(Integer.parseInt(array[0]),
Integer.parseInt(array[1]));
pointArray.add(p);
}
}
/**
* 计算坐标点对于2个簇中心点的隶属度
*
* @param p
* 待测试坐标点
*/
private void computeMemberShip(Point p) {
// p点距离第一个簇中心点的距离
double distance1 = 0;
// p距离第二个中心点的距离
double distance2 = 0;
// 用欧式距离计算
distance1 = Math.pow(p.getX() - p1.getX(), 2)
+ Math.pow(p.getY() - p1.getY(), 2);
distance2 = Math.pow(p.getX() - p2.getX(), 2)
+ Math.pow(p.getY() - p2.getY(), 2);
// 计算对于p1点的隶属度,与距离成反比关系,距离靠近越小,隶属度越大,所以要用大的distance2另外的距离来表示
p.setMemberShip1(distance2 / (distance1 + distance2));
// 计算对于p2点的隶属度
p.setMemberShip2(distance1 / (distance1 + distance2));
}
/**
* 执行期望最大化步骤
*/
public void exceptMaxStep() {
// 新的优化过的簇中心点
double p1X = 0;
double p1Y = 0;
double p2X = 0;
double p2Y = 0;
double temp1 = 0;
double temp2 = 0;
// 误差值
double errorValue1 = 0;
double errorValue2 = 0;
// 上次更新的簇点坐标
Point lastP1 = null;
Point lastP2 = null;
// 当开始计算的时候,或是中心点的误差值超过1的时候都需要再次迭代计算
while (lastP1 == null || errorValue1 > 1.0 || errorValue2 > 1.0) {
for (Point p : pointArray) {
computeMemberShip(p);
p1X += p.getMemberShip1() * p.getMemberShip1() * p.getX();
p1Y += p.getMemberShip1() * p.getMemberShip1() * p.getY();
temp1 += p.getMemberShip1() * p.getMemberShip1();
p2X += p.getMemberShip2() * p.getMemberShip2() * p.getX();
p2Y += p.getMemberShip2() * p.getMemberShip2() * p.getY();
temp2 += p.getMemberShip2() * p.getMemberShip2();
}
lastP1 = new Point(p1.getX(), p1.getY());
lastP2 = new Point(p2.getX(), p2.getY());
// 套公式计算新的簇中心点坐标,最最大化处理
p1.setX(p1X / temp1);
p1.setY(p1Y / temp1);
p2.setX(p2X / temp2);
p2.setY(p2Y / temp2);
errorValue1 = Math.abs(lastP1.getX() - p1.getX())
+ Math.abs(lastP1.getY() - p1.getY());
errorValue2 = Math.abs(lastP2.getX() - p2.getX())
+ Math.abs(lastP2.getY() - p2.getY());
}
System.out.println(MessageFormat.format(
"簇中心节点p1({0}, {1}), p2({2}, {3})", p1.getX(), p1.getY(),
p2.getX(), p2.getY()));
}
}
坐标点Point类:/**
* 坐标点类
*
* @author lyq
*
*/
public class Point {
// 坐标点横坐标
private double x;
// 坐标点纵坐标
private double y;
// 坐标点对于P1的隶属度
private double memberShip1;
// 坐标点对于P2的隶属度
private double memberShip2;
public Point(double d, double e) {
this.x = d;
this.y = e;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x = x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y = y;
}
public double getMemberShip1() {
return memberShip1;
}
public void setMemberShip1(double memberShip1) {
this.memberShip1 = memberShip1;
}
public double getMemberShip2() {
return memberShip2;
}
public void setMemberShip2(double memberShip2) {
this.memberShip2 = memberShip2;
}
}
调用类;/**
* EM期望最大化算法场景调用类
* @author lyq
*
*/
public class Client {
public static void main(String[] args){
String filePath = "C:\\Users\\lyq\\Desktop\\icon\\input.txt";
EMTool tool = new EMTool(filePath);
tool.readDataFile();
tool.exceptMaxStep();
}
}
输出结果:簇中心节点p1(7.608, 5.907), p2(14.208, 8.745)在这个程序中,隐藏变量就是簇中心点,通过不断的迭代计算,最终无限的接近真实值,相当有意思的算法。