Dijkstra的邻接表表示算法

有一个给定的图G(V,E)及其邻接列表表示形式，并且还提供了一个源顶点。Dijkstra的算法，用于找到源顶点与图G的任何其他顶点之间的最小最短路径。

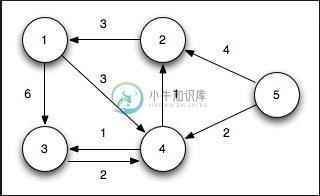
为了解决这个问题，我们将使用两个列表。一种是存储已被视为最短路径树的顶点，另一种将保存尚未被考虑的顶点。在算法的每个阶段，我们都找到未考虑的顶点，并且顶点与源的距离最小。

另一个列表用于保存前任节点。使用先前节点，我们可以找到从源到目标的路径。

Dijkstra最短路径算法的复杂度为O（E log V），因为该图是使用邻接表表示的。这里E是边数，V是顶点数。

输入输出

Input:
The adjacency list of the graph with the cost of each edge.Output:
0 to 1, Cost: 3 Previous: 0
0 to 2, Cost: 5 Previous: 1
0 to 3, Cost: 4 Previous: 1
0 to 4, Cost: 6 Previous: 3
0 to 5, Cost: 7 Previous: 2
0 to 6, Cost: 7 Previous: 4

算法

dijkstraShortestPath(g : Graph, dist, prev, start : node)

输入-图形g，用于存储距离的dist列表，先前节点的prev列表以及起始顶点。

输出- 从起点到所有其他顶点的最短路径。

Begin
   for all vertices u in (V - start) do
      dist[u] := ∞
      prev[u] := φ
   done

   set dist[start] = 0 and prev[start] := φ

   for all node u in V do
      insert u into queue ‘Q’.
   done

   while Q is not empty do
      u := minimum element from Queue
      delete u from Q
      insert u into set S

      for each node v adjacent with node u do
         if dist[u]+cost(v) < dist[v] then
            dist[v] := dist[u]+cost(v)
            prev[v] := u
      done
   done
End

示例

#include<iostream>
#include<set>
#include<list>
#include<algorithm>
using namespace std;

typedef struct nodes {
   int dest;
   int cost;
}node;

class Graph {
   int n;
   list<node> *adjList;
   private:
      void showList(int src, list<node> lt) {
         list<node> :: iterator i;
         node tempNode;

         for(i = lt.begin(); i != lt.end(); i++) {
            tempNode = *i;
            cout << "(" << src << ")---("<<tempNode.dest << "|"<<tempNode.cost<<") ";
         }
         cout << endl;
      }
   public:
      Graph() {
         n = 0;
      }

      Graph(int nodeCount) {
         n = nodeCount;
         adjList = new list<node>[n];
      }

      void addEdge(int source, int dest, int cost) {
         node newNode;
         newNode.dest = dest;
         newNode.cost = cost;
         adjList[source].push_back(newNode);
      }

      void displayEdges() {
         for(int i = 0; i<n; i++) {
            list<node> tempList = adjList[i];
            showList(i, tempList);
         }
      }

      friend void dijkstra(Graph g, int *dist, int *prev, int start);
};

void dijkstra(Graph g, int *dist, int *prev, int start) {
   int n = g.n;

   for(int u = 0; u<n; u++) {
      dist[u] = 9999;   //set as infinity
      prev[u] = -1;    //undefined previous
   }

   dist[start] = 0;   //distance of start is 0
   set<int> S;       //create empty set S
   list<int> Q;

   for(int u = 0; u<n; u++) {
      Q.push_back(u);    //add each node into queue
   }

   while(!Q.empty()) {
      list<int> :: iterator i;
      i = min_element(Q.begin(), Q.end());
      int u = *i; //the minimum element from queue
      Q.remove(u);
      S.insert(u); //add u in the set
      list<node> :: iterator it;

      for(it = g.adjList[u].begin(); it != g.adjList[u].end();it++) {
         if((dist[u]+(it->cost)) < dist[it->dest]) { //relax (u,v)
            dist[it->dest] = (dist[u]+(it->cost));
            prev[it->dest] = u;
         }
      }
   }
}

main() {
   int n = 7;
   Graph g(n);
   int dist[n], prev[n];
   int start = 0;

   g.addEdge(0, 1, 3);
   g.addEdge(0, 2, 6);
   g.addEdge(1, 0, 3);
   g.addEdge(1, 2, 2);
   g.addEdge(1, 3, 1);
   g.addEdge(2, 1, 6);
   g.addEdge(2, 1, 2);
   g.addEdge(2, 3, 1);
   g.addEdge(2, 4, 4);

   g.addEdge(2, 5, 2);
   g.addEdge(3, 1, 1);
   g.addEdge(3, 2, 1);
   g.addEdge(3, 4, 2);
   g.addEdge(3, 6, 4);
   g.addEdge(4, 2, 4);
   g.addEdge(4, 3, 2);
   g.addEdge(4, 5, 2);
   g.addEdge(4, 6, 1);
   g.addEdge(5, 2, 2);
   g.addEdge(5, 4, 2);
   g.addEdge(5, 6, 1);
   g.addEdge(6, 3, 4);
   g.addEdge(6, 4, 1);
   g.addEdge(6, 5, 1);

   dijkstra(g, dist, prev, start);

   for(int i = 0; i<n; i++)
      if(i != start)
         cout<<start<<" to "<<i<<", Cost: "<<dist[i]<<" Previous: "<<prev[i]<<endl;
}

输出结果

0 to 1, Cost: 3 Previous: 0
0 to 2, Cost: 5 Previous: 1
0 to 3, Cost: 4 Previous: 1
0 to 4, Cost: 6 Previous: 3
0 to 5, Cost: 7 Previous: 2
0 to 6, Cost: 7 Previous: 4