用向量和对表示邻接表图

Question

在书中，他们做过这样的宣示：

#include <iostream>
#include <vector>
using namespace std;
typedef pair<int, int> ii;
typedef vector<ii> vii;
vector <vii> AdjList;

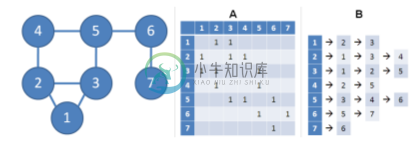
我应该如何将下面图的输入作为邻接表并输出它的邻接表表示？假设，edge的每个成本是10。

Answer 1

#include<iostream>
#include<vector>
using namespace std;
typedef vector<int> vi;
typedef pair<int,int> ii;
typedef vector<ii> vii;

int main()
{
   int n,m ; 
   cin>>n>>m;
   vector<vii> adjList(n+1); //For vertex 1...n
   //Reading edges for the input for graph
   for(int i=0;i<m;i++)
   {
      int u,v;
      cin>>u>>v;
    /*Here u->v is the edge and pair second term can be used to store weight in
      case of weighted graph.
    */
      adjList[u].push_back(make_pair(v,10));
   }
   //To print the edges stored in the adjacency list
   for(int i=1;i<=n;i++)
   {
       for(int j=0;j<(int)adjList[i].size();j++)
       {
           cout<<"Edge is "<<i<<" -> "<<adjList[i][j].first<<endl;
           cout<<"Weight is "<<adjList[i][j].second<<endl;
       }
   }
   return 0;
}