如何使用邻接表来表示具有虚拟顶点的图？

Question

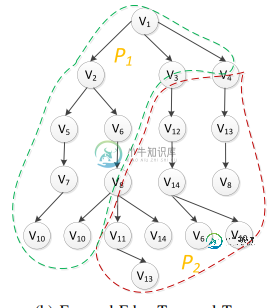
此图包含虚拟顶点。如何使用邻接表存储顶点的状态信息？应该存储每个顶点的输出边。

我用了简单的邻接表。但在这里，例如，v14有两组不同的输出边（一组没有输出边，另一组有两个输出边）。我应该使用什么数据结构来表示这样的虚拟节点。

Answer 1

由于您对实现没有约束，一个简单的类就可以了。在这里，我们将指向子级的（共享）指针存储在一个向量中。（重载）AddChild方法返回对添加的子项的引用，因此更容易将AddChild链接在一起。使用的操作符重载很好，但不是必需的，如果需要，您可以删除它们。代码如下：

#include <utility>
#include <iostream>
#include <string>
#include <vector>
#include <memory>

using std::vector;
using std::string;
using std::size_t;
using std::shared_ptr;
using std::make_shared;
using std::ostream;
using std::cout;
using std::endl;

class Node {
public:
  using child_ptr_type = shared_ptr<Node>;
  using contaner_type = vector<child_ptr_type >;

  explicit Node(string lab = "Default", contaner_type ch = {})
  : label(std::move(lab))
  , children(std::move(ch))
  {}

  const string &getLabel() const
  { return label; }

  void setLabel(const string &label)
  { Node::label = label; }

  const contaner_type &getChildren() const
  { return children; }

  const Node& getChild(size_t indx) const
  { return *children[indx]; }

  Node& getChild(size_t indx)
  { return *children[indx]; }

  Node& addChild(const string& lab = "Default", const contaner_type & ch = {})
  {
    children.push_back(make_shared<Node>(lab, ch));
    return *children.back();
  }

  Node& addChild(const child_ptr_type &child)
  {
    children.push_back(child);
    return *children.back();
  }

  Node& addChild(const Node& node)
  {
    children.push_back(make_shared<Node>(node));
    return *children.back();
  }

  friend ostream& operator<<(ostream& os, const Node &node)
  {
    node.print(os);
    return os;
  }

  Node&operator[](size_t indx)
  {
    return getChild(indx);
  }

  const Node&operator[](size_t indx) const
  {
    return getChild(indx);
  }



private:
  string label;
  contaner_type children;
  void print(ostream& os, size_t level = 0) const
  {
    for (size_t i = 0; i != level; ++i) {
      os << "|----";
    }
    os << label << '\n';
    for (const auto& child : children) {
      child->print(os, level + 1);
    }
  }
};

int main()
{
  Node V1("V1");

  V1.addChild("V2").addChild("V5").addChild("V7").addChild("V10");
  V1[0].addChild("V6").addChild("V8").addChild("V10");

  V1[0][1][0].addChild("V11").addChild("V13");
  V1[0][1][0].addChild("V14");

  V1.addChild("V3").addChild("V12").addChild("V14").addChild("V6");
  V1[1][0][0].addChild("V10");

  V1.addChild("V4").addChild("V13").addChild("V8");

  cout << V1 << endl;
  return 0;
}

main中的树是您在图片中的示例。输出如下：

V1
|----V2
|----|----V5
|----|----|----V7
|----|----|----|----V10
|----|----V6
|----|----|----V8
|----|----|----|----V10
|----|----|----|----V11
|----|----|----|----|----V13
|----|----|----|----V14
|----V3
|----|----V12
|----|----|----V14
|----|----|----|----V6
|----|----|----|----V10
|----V4
|----|----V13
|----|----|----V8