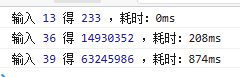
前端 - 如何用 useMemo 优化这个斐波那契计算的写法？

Question

import React from "react";

function fibonacci(n: number): number {
  return n < 2 ? n : fibonacci(n - 1) + fibonacci(n - 2);
}

function FibonacciExample() {
  const [inputValue, setInputValue] = React.useState(0);

  function handleClick() {
    let time = new Date().getTime();
    console.log(
      fibonacci(inputValue),
      `耗时：${new Date().getTime() - time}ms`
    );
  }

  return (
    <div>
      <input
        type="number"
        value={inputValue}
        onChange={(event) => setInputValue(Number(event.target.value))}
      />
      <button onClick={handleClick}>计算 fibonacci</button>
    </div>
  );
}

export default FibonacciExample;

在网上搜 React.useMemo 和 React.memo 的区别，发现有这么个斐波那契的例子，是否可以用 useMemo 来优化性能？

Answer 1

就是把缓存法的缓存放到了useMemo里...

const fibnacci = useMemo(()=>{
    const cache = {}
    const fib = (n: number) => {
        if(n in cache) return cache[n];
        if(n < 2) return n;
        const result = fib(n-1) + fib(n-2);
        cache[n] = result;
        return result;
    }
    return fib;
}, [])

Answer 2

import React, { useCallback, useState } from "react";

function fibonacci(n: number): number {
  return n < 2 ? n : fibonacci(n - 1) + fibonacci(n - 2);
}

function FibonacciExample() {
  const [inputValue, setInputValue] = useState(0);
  const [result, setResult] = useState(0);

  const handleClick = useCallback(() => {
    let time = new Date().getTime();
    const fibResult = fibonacci(inputValue);
    console.log(fibResult, `耗时：${new Date().getTime() - time}ms`);
    setResult(fibResult);
  }, [inputValue]);

  return (
    <div>
      <input
        type="number"
        value={inputValue}
        onChange={(event) => setInputValue(Number(event.target.value))}
      />
      <button onClick={handleClick}>计算 fibonacci</button>
      <p>结果：{result}</p>
    </div>
  );
}

export default FibonacciExample;

2.:

import React, { useMemo, useState, useCallback } from "react";

function useFibonacciMemo() {
  const fibMemo = useMemo(() => {
    const cache = {};

    const fib = (n) => {
      if (n in cache) return cache[n];
      if (n < 2) return n;
      const result = fib(n - 1) + fib(n - 2);
      cache[n] = result;
      return result;
    };

    return fib;
  }, []);

  return fibMemo;
}

function FibonacciExample() {
  const [inputValue, setInputValue] = useState(0);
  const [result, setResult] = useState(0);
  const fibMemo = useFibonacciMemo();

  const handleClick = useCallback(() => {
    let time = new Date().getTime();
    const fibResult = fibMemo(inputValue);
    console.log(fibResult, `耗时：${new Date().getTime() - time}ms`);
    setResult(fibResult);
  }, [inputValue, fibMemo]);

  return (
    <div>
      <input
        type="number"
        value={inputValue}
        onChange={(event) => setInputValue(Number(event.target.value))}
      />
      <button onClick={handleClick}>计算 fibonacci</button>
      <p>结果：{result}</p>
    </div>
  );
}

export default FibonacciExample;

Answer 3

useMemo 只是用来减少不必要的运算， 你这里的问题是：对于fibonacci 运算来说，它本身运算大参数耗时就很长了，要么你不要使用js算fibonacci，换成 webassembly 之类的，要么，提前算好放到静态字典里，需要时候直接取，反正，就你javascript整数范围内能够算得出的 数据也没多少组很有限。

如果你要体验useMemo的优势，主要考虑的是子组件需要传递参数比如onChange之类的函数使用useMemo包装 可以减少重新渲染子组件次数。 上面提供的例子是对的，但是由于你每次都修改inputValue，所以每次都得重新构建handleClick，一次都没省。

Answer 4

对于这个问题，我想你想问的是假如有高负载计算时要怎么保持界面的交互性,因为就你问的这个具体问题解决起来非常简单，要计算一个斐波那契数可以使用O(N)的算法实现比如

function fib(n: number): number {
  if (n === 0) return 0
  let minusTwo = 0
  let minusOne = 1

  for (let i = 2; i <= n; ++i) {
    const temp = minusOne + minusTwo
    minusTwo = minusOne
    minusOne = temp
  }

  return minusOne
}

考虑到斐波那契数膨胀的非常快如果仅仅是要求double能精准表示的斐波那契数完全可以使用打表实现O(1)的时间复杂度求斐波那契数，但是如果你想要知道有没有通用的方法，那么下面的方法可能是你需要的

1. 优化算法

就你问的这个具体的完全可以通过优化算法而不用采取其他任何其他手段就能达到很好的效果

2. 开线程或进程

如果你能权衡好进程或者线程之间通信和同步的成本或者仅仅是不想阻塞页面那么开线程或进程是解决问题的最简单的方式

3. 将任务分成多个子任务分批的完成

这个做法非常灵活，可以通过不同的方式实现就你举得这个例子可以通过以下代码实现, 可以先把递归的方式转换为迭代的方式(这样比较好控制执行流)，并且每次执行任务时设置一个时间片，时间片用尽就主动交出执行权这样就算是在单线程的情况下也能保证页面的交互性在线体验地址

const delay = (ms: number) =>
  new Promise<void>((r) => setTimeout(() => r(), ms));

async function fibonacci(n: number): number {
  if (n < 2) return n;

  enum Op {
    Add,
    Calc
  }
  type Task = {
    op: Op;
    value: any;
  };

  const taskStack: Task[] = [];
  const valueStack: number[] = [];

  taskStack.push({
    op: Op.Calc,
    value: n
  });

  let last = performance.now();
  const MIN_TIME_SLICE = 5;
  let currentTimeSlice = 100;
  let remainingTime = currentTimeSlice;
  while (taskStack.length) {
    const now = performance.now();
    remainingTime -= now - last;
    const shouldYield = remainingTime <= 0;
    if (shouldYield) {
      await delay(0);
      // 长时间不能算出来的降低它的优先级(减少它的时间切片)
      currentTimeSlice /= 2;
      remainingTime = Math.max(currentTimeSlice, MIN_TIME_SLICE);
      last = now;
    }

    const { op, value } = taskStack.pop();
    switch (op) {
      case Op.Calc: {
        if (value < 2) {
          valueStack.push(value);
        } else {
          taskStack.push({
            op: Op.Add,
            value: undefined
          });
          taskStack.push({
            op: Op.Calc,
            value: value - 2
          });
          taskStack.push({
            op: Op.Calc,
            value: value - 1
          });
        }
        break;
      }
      case Op.Add: {
        let a = valueStack.pop();
        let b = valueStack.pop();
        valueStack.push(a + b);
        break;
      }
      default:
        throw new Error("Not reachable");
    }
  }

  return valueStack[0];
}

function FibonacciExample() {
  const [inputValue, setInputValue] = React.useState(0);

  async function handleClick() {
    let time = new Date().getTime();
    const ans = await fibonacci(inputValue);
    console.log(ans, `耗时：${new Date().getTime() - time}ms`);
  }

  return (
    <div>
      <input
        type="number"
        value={inputValue}
        onChange={(event) => setInputValue(Number(event.target.value))}
      />
      <button onClick={handleClick}>计算 fibonacci</button>
    </div>
  );
}