斐波那契树-计算机程序结构和解释中的递归

Question

在Abelson/Sussman的经典文本《计算机程序的结构和解释》中，在第1.2.2节关于树递归和斐波那契序列的内容中，他们展示了以下图像：

计算第五个斐波那契数时生成的树递归过程

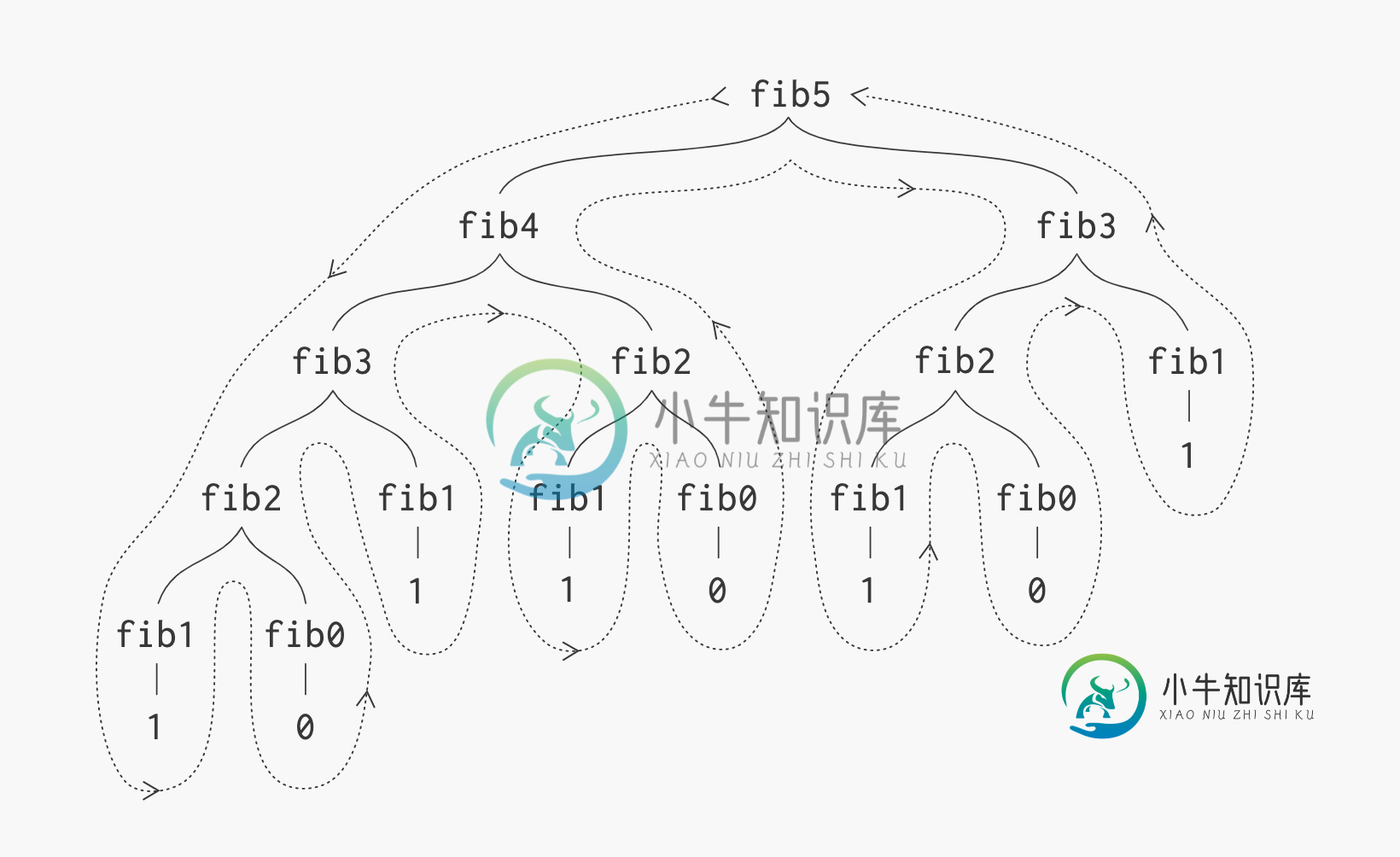
然后他们写道：“请注意，整个计算过程（fib 3）-几乎一半的工作-都是重复的。事实上，不难证明程序将计算的次数（fib 1）或（fib 0）（通常，上述树中的叶子数）正是fib（n 1）。”

我知道他们正在强调树递归以及斐波那契树递归的这个经典案例是如何低效的，因为递归函数调用了自己两次：

计算斐波那契数的树递归函数

我的问题是，为什么很明显（即“不难证明”）树叶的数量等于序列中的下一个斐波那契数？我可以从视觉上看到情况是这样的，但我没有看到叶子数量（减少的fib 1和fib 0计算）为什么应该是下一个Fibonacci数（在本例中为fib 6，即第六个Fibonacci数，即fib n 1，其中n为5）的指标的联系。

很明显，斐波那契序列是如何计算的——序列中前两个数字的总和产生当前数字，但为什么叶子的数量恰好等于序列中的下一个数字？这里的联系是什么（除了显而易见的联系，观察它并将1和0叶相加，实际上，在这种情况下，总计数为8，这是下一个（第6个）斐波那契数，依此类推）？

Answer 1

我们可以通过外推来证明这一点。

Fib（0）=1的叶数。Fib（1）=1的叶数。

现在，表达式Fib（2）基本上是Fib（1）Fib（0）的和，即，Fib（2）=Fib（1）Fib（0）。因此，从树本身可以看出，对于Fib（2）的叶子数等于Fib（1）和Fib（0）的叶子总数。因此，Fib（2）的叶数等于2。

接下来，对于Fib（3），叶子数将是Fib（2）和Fib（1）的叶子总和，即2 1=3

正如你们现在已经观察到的，这遵循一种类似于斐波那契级数的模式。事实上，如果我们将Fib（n）的叶数定义为FibLeaves（n），那么我们可以看到这个序列左移了1个空间。

<代码>Fib（n）=0，1，1，2，3，5，8，13，21

FibLeaves（n）=1，1，2，3，5，8，13，21

因此，叶的数量将等于Fib（n 1）

Answer 2

n=1子句的数量必须等于fib（n），因为这是唯一一个非零数字来自的地方，如果一些1的总和等于fib（n），则其中必须有fib（n）。

由于fib（n 1）=fib（n）fib（n-1），我们只需要证明计算fib（0）的fib（n-1）叶。我不太清楚如何证明这一点，但它可能从上一个案例中归纳出来？

也许一种更简单的方法是归纳式地完成整个过程。

对于我们的基本情况：

• N=0：树中有fib（N 1）=fib（1）=1片叶子。通过检查证明
• N=1：树中有fib（N 1）=fib（2）=1片叶子。通过检查证明

归纳步骤：为了计算任意N的fib（N），我们计算一次fib（N-1）和一次fib（N-2），并将其结果相加。通过归纳，树中有fib（N）叶来自我们对fib（N-1）的计算，树中有fib（N-1）叶来自我们对fib（N-2）的计算。

因此，在我们的整个树中有fib（N）fib（N-1）叶子，它等于fib（N 1）。QED。

Answer 3

“不难表现”比“显而易见”更难。

使用两种基本情况的归纳法<让我们调用Fib（x），Fib01（x）中的计算数<然后，

Fib01(0) = 1 by definition, which is Fib(1) 
Fib01(1) = 1 by definition, which is Fib(2)

Fib01(n) = Fib01(n-1) + Fib01(n-2) 
         = Fib(n) + Fib(n-1) 
         = Fib(n+1) by definition

QED。