从笛卡尔坐标到极坐标的图像转换

Question

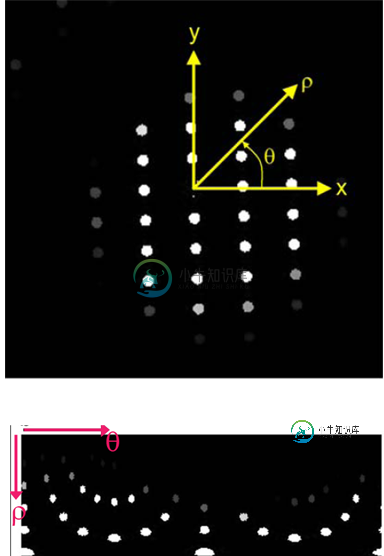
我想知道是否有人帮助我理解如何将顶部图像转换为底部图像。以下链接中提供了这些图像。顶部图像采用笛卡尔坐标。底部图像是极坐标中的转换图像

Answer 1

这是一个基本的直角坐标到极坐标的变换。要进行转换，请扫描输出图像，并将x和y视为r和θ。然后使用它们作为r和θ，在输入图像中查找相应的像素。这样的话：

int x, y;
for (y = 0; y < outputHeight; y++)
{
    Pixel* outputPixel = outputRowStart (y); // <- get a pointer to the start of the output row
    for (x = 0; x < outputWidth; x++)
    {
        float r = y;
        float theta = 2.0 * M_PI * x / outputWidth;
        float newX = r * cos (theta);
        float newY = r * sin (theta);
        *outputPixel = getInputPixel ( newX, newY ); // <- Should probably do at least bilinear resampling in this function
        outputPixel++;
    }
}

请注意，您可能希望根据您试图实现的目标来处理换行。θ值换行为2pi。