MATLAB中极坐标图像到笛卡尔图像的转换

Question

我无法将[R，theta]格式的图像转换为[x，y]

我正在尝试使用interp2。

[nZ,nX] = size(im);
theta = ((0:(nX-1)))*0.0071; %0.0071 is known angular separation of columns
rr = (0:(nZ-1))*0.0039; %0.0039 is resolution of rows

然后我会：

%% Create grids and convert polar coordinates to rectangular
[THETA,RR] = meshgrid(theta,rr);
[XX,YY] = pol2cart(THETA,RR);

最后：

im_out=interp2(theta,rr,im,XX,YY,'linear');
im_out(isnan(im_out)) = 0;

但图像不正确！

以下是输入图像（图1）（带R，θ几何）：

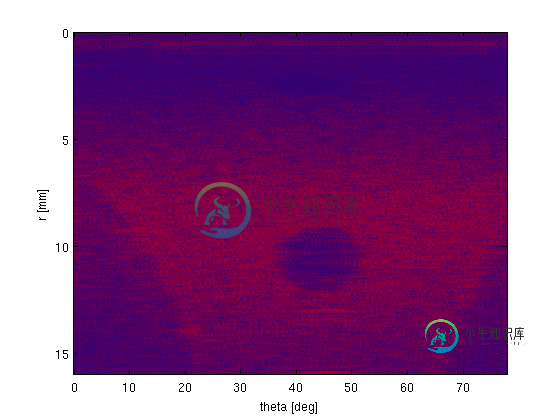
我想在笛卡尔网格上重建它（使用interp2），所以它看起来像这样（图2）：

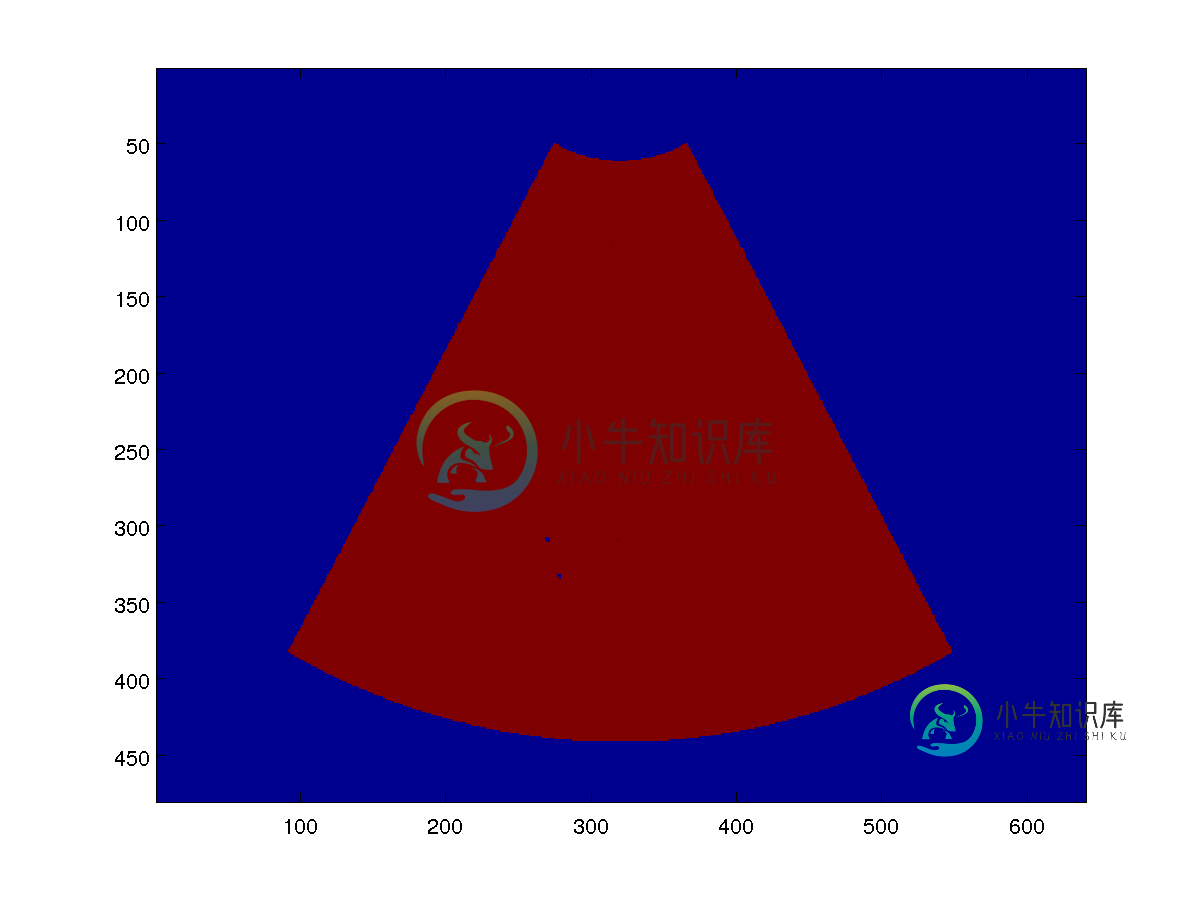
极坐标图像（图1）中的所有数据应映射到笛卡尔图像的红色部分（图2）。

Answer 1

我设法做到了以下几点：

我在im矩阵的顶部添加了零，以正确定义曲率半径（在我的例子中为1018个像素，即ROC）和极坐标原点：

im = IML';   % scan_lines (rotated for now)
sector=75;   % [degrees]
im_depth=16; % [cm] (depth + ROC)

ROC=3.98;
im_depth=16+ROC;

col_size=size(im,2);
zeros_row = zeros(1018, col_size);
im=[zeros_row; im];
scan_lines = im;

[nY, nX] = size(im);

min_ang=(sector/nX)*pi/180;% [rad.]
theta = -nX/2*min_ang:min_ang:nX/2*min_ang; % total angle/num. lines [radians]
theta = theta(2:end);

steering_angles=theta; % angles [radians]

num_samples=im_depth/nY;
rr = (0:(nY-1))*num_samples; % im. depth/num. samples
r = rr; 

image_size = [26.15,16+ROC]; % [cm]

x_resolution = 480; % image resolution [pix]
y_resolution = 640;

% assign the inputs
x = image_size(2);
y = image_size(1);

disp_rr=max(rr)/(im_depth-ROC);

%plot input image
%subplot(1,2,1); imagesc(theta*(180/pi), rr/disp_rr, fliplr(IML')); title('polar geometry'); colormap(gray)
%xlabel('theta [deg]')
%ylabel('r [cm]'); hold on;

% number of scan lines
Nt = length(scan_lines(1, :));

% create regular Cartesian grid to remap to
pos_vec_y_new = (0:1/(y_resolution-1):1).*y - y/2;
pos_vec_y_new = pos_vec_y_new';
pos_vec_x_new = (0:1/(x_resolution-1):1).*x;
[pos_mat_x_new, pos_mat_y_new] = ndgrid(pos_vec_x_new, pos_vec_y_new);

% convert new points to polar coordinates
[th_cart, r_cart] = cart2pol(pos_mat_x_new, pos_mat_y_new);

% interpolate using linear interpolation
op = interp2(steering_angles,r, scan_lines, th_cart, r_cart, 'linear').';

% set any values outside of the interpolation range to be 0
% op(isnan(op)) = max(b_mode(:));
op(isnan(op)) = 0;

%plot output image
subplot(2,2,4); 
imagesc(pos_vec_y_new, pos_vec_x_new-ROC, op'); title('Cartesian geometry'); colormap(gray); 
xlabel('lat [cm]')
ylabel('ax [cm]');
caxis([7.2,max(max(op))])