将图像从笛卡尔转换为极地

Question

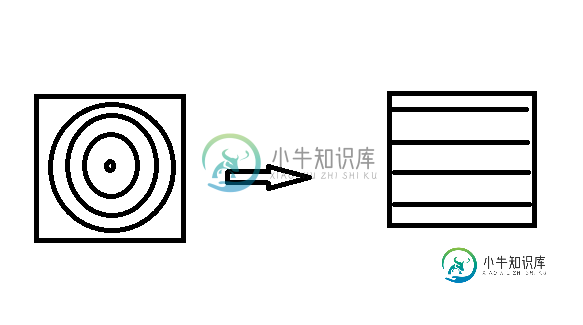
我正在尝试将一个包含许多圆心相同的圆的图像从笛卡尔坐标转换为极坐标（这样新图像将是圆，但是线，而不是圆，请参见下图），使用以下代码可以很好地解决这一问题：

[r, c] = size(img);
r=floor(r/2);
c=floor(c/2);
[X, Y] = meshgrid(-c:c-1,-r:r-1);
[theta, rho] = cart2pol(X, Y); 
subplot(221), imshow(img), axis on;
hold on;
subplot(221), plot(xCenter,yCenter, 'r+');
subplot(222), warp(theta, rho, zeros(size(theta)), img);
view(2), axis square;

问题是，我不明白为什么它会起作用？（显然这不是我的代码），我的意思是，当我使用函数cart2pol时，我甚至没有使用图像，它只是一些由meshgrid函数生成的向量x和y。。另一个问题是，我想以某种方式得到一个新图像（不仅仅是能够用wrap函数绘制），它是原始图像，而是θ和ρ坐标（意味着相同的像素，但经过重新排列）。。。我甚至不知道该怎么问这个问题，最后我想得到一个图像，它是一个矩阵，这样我可以对每一行求和，并将矩阵转换为列向量。。。

Answer 1

你可以把你的图像想象成一个2D矩阵，其中每个像素都有一个X和Y坐标

[(1,1)    (1,2)    (1,3)   ....   (1,c)]
[(2,1)    (2,2)    (2,3)   ....   (2,c)]
[(3,1)    (3,2)    (3,3)   ....   (3,c)]
[....     ....     ....    ....   .... ]
[(r,1)    (r,2)    (r,3)   ....   (r,c)]

在您发布的代码中，它将这些（X，Y）坐标中的每一个映射到其等效极坐标（R，θ），使用图像的中心地板（c/2）和地板（R/2）作为参考点。

% Map pixel value at (1,1) to it's polar equivalent
[r,theta] = cart2pol(1 - floor(r/2),1 - floor(c/2));

因此，（1,1）使用的任何像素值现在都应该出现在新的极坐标空间中，位于（r，θ）。重要的是要注意，要进行此转换，有关图像中实际像素值的信息无关紧要，我们只想对图像中的每个像素执行此转换。

所以首先我们要找出图像的中心在哪里：

[r, c] = size(img);
r = floor(r / 2);
c = floor(c / 2);

然后我们计算出图像中每个点的（X， Y）坐标（在中心已经被减去之后

[X, Y] = meshgrid(-c:c-1,-r:r-1);

现在将所有这些笛卡尔点转换为极坐标

[theta, rho] = cart2pol(X, Y); 

warp现在所做的就是说“在（θ，ρ）的相应位置显示（X，Y）处img的值”

warp(theta, rho, zeros(size(theta)), img);

现在似乎您想要一个维度为[nTheta， nRho]的新2D图像。为此，您可以使用griddata将分散（θ， rho）图像（由上面的warp显示）插值到常规网格。

% These is the spacing of your radius axis (columns)
rhoRange = linspace(0, max(rho(:)), 100);

% This is the spacing of your theta axis (rows)
thetaRange = linspace(-pi, pi, 100);

% Generate a grid of all (theta, rho) coordinates in your destination image
[T,R] = meshgrid(thetaRange, rhoRange);

% Now map the values in img to your new image domain
theta_rho_image = griddata(theta, rho, double(img), T, R);

查看griddata的所有插值方法，找出哪种方法最适合您的场景。

还有几个其他问题（如中心的四舍五入）导致结果略有错误。下面提供了一个完整的工作示例

% Create an image of circles
radii = linspace(0, 40, 10);

rows = 100;
cols = 100;
img = zeros(rows, cols);

for k = 1:numel(radii)
    t = linspace(0, 2*pi, 1000);
    xx = round((cos(t) * radii(k)) + (cols / 2));
    yy = round((sin(t) * radii(k)) + (rows / 2));

    toremove = xx > cols | xx < 1 | yy > rows | yy < 1;

    inds = sub2ind(size(img), xx(~toremove), yy(~toremove));

    img(inds) = 1;
end

[r,c] = size(img);
center_row = r / 2;
center_col = c / 2;

[X,Y] = meshgrid((1:c) - center_col, (1:r) - center_row);

[theta, rho] = cart2pol(X, Y);

rhoRange = linspace(0, max(rho(:)), 1000);
thetaRange = linspace(-pi, pi, 1000);

[T, R] = meshgrid(thetaRange, rhoRange);

theta_rho_image = griddata(theta, rho, double(img), T, R);

figure
subplot(1,2,1);
imshow(img);
title('Original Image')

subplot(1,2,2);
imshow(theta_rho_image);
title('Polar Image')

结果呢