在给定图中求最小值域生成树的算法
给出加权无向图G(v,e)的权值为w(e),求出使每对顶点(u,v)∈G连通(简言之为生成树)且所选边的权值范围最小(或最小权值与最大权值之差最小)的边集。
我尝试了贪婪的方法,根据权重对边进行排序,然后在排序的数组中选择连续边之间权重差最小的两条边(G[index=current_left],G[index+1=current_right]),然后根据(current_left,current_left-J)或(current_right+J)之间的最小差向左或向右移动,其中J)递增,直到找到至少有一个未访问顶点的边。
例如:
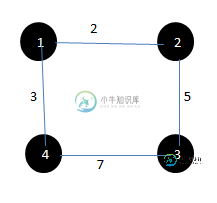
共有1个答案
您应该能够在O(E*(MST计算的成本)):
T = no tree
for all edge weights w_fix sorted in ascending order:
for all edges e:
if w(e) >= w_fix:
set w'(e) = w(e) - w_fix
else:
set w'(e) = infinity
find MST T' according to w'
if T == no tree or max edge weight(T) > max edge weight(T'):
set T := T'
print T
其思想是:在最优生成树中,边权必须是边权的最小值;因此,确定一个最小边缘权重,并找到一个MST只包含比该权重更重的边缘。因为所有的MSTs也是最小瓶颈生成树,所以这是可行的。
这里有一个改进,在对数平方因子下是最佳的;基本思想不变。
sort edge array E[] by increasing weights
low := high := 0
opt_low := opt_high := 0
opt := infinity
connected := false
while (high < E.length - 1) or (connected):
if not connected:
high = high + 1
else:
low = low + 1
update(connected)
if connected:
if E[high].weight - E[low].weight < opt:
opt = E[high].weight - E[low].weight
opt_low = low
opt_high = high
print(opt, opt_low, opt_high)
这个想法是在边缘上保持一个滑动窗口,并使用连通性来维护窗口。为了维护连接性信息,您将使用特殊的数据结构。其中有许多数据结构允许多对数的时间开销来维护删除和添加边的连通性信息,你可以在MIT6.851课堂讲稿中找到这些数据结构的信息。
-
我需要一些关于Prim的算法问题的帮助: 设T是图G的一个由Prim算法得到的最小生成树。设Gnew是在G上增加一个新的顶点和一些带权的边,将新的顶点连接到G上的一些顶点而得到的图,我们能把其中一条新的边加到T上构造Gnew的最小生成树吗?如果你回答是,请解释是怎样做的;如果没有,请解释原因。 提前谢谢!!
-
这里有一个图,我需要用Prim和Kruskal的算法找到G的最小生成树。 我用普里姆的算法找到了最小生成树。这是我的尝试。 我很难用Kruskal的算法找到最小生成树。我看过许多与Kruskal的图算法相关的视频,但最终得到的图与Prim的算法相同。 谁能给我演示一下如何用Kruskal的算法找到图的最小生成树吗?
-
假设我选择V(H)={a,e,f}和e(H)={ae,af,fe} 现在,对于每条边e∈e(H),我们用e'记下了(来自原始图G的) 达到这个最小值的边。所以E'={bc,df,eg},因为bc=4,df=9,eg=8,是连接我的元件的最小边。我在H中有一个相对于代价函数C′的最小生成树,而a′是这棵树的边集。 但是我的A'的边和E'的没有一条是一样的。
-
考虑一个有n个顶点和m条边的无向图。假设边有两种类型:m1红色边和m2绿色边。因此m=m1+m2。红色边缘的权重为1,绿色边缘的权重为2。设计并分析了一种计算这种图的最小生成树的有效算法
-
无向图最小生成树的Prim算法 思路说明 假设点A,B,C,D,E,F,两点之间有连线的,以及它们的距离分别是:(A-B:7);(A-D:5);(B-C:8);(B-D:9);(B-E:7);(C-E:5);(D-E:15);(D-F:6);(E-F:8);(E-G:9);(F-G:11) 关于Prim算法的计算过程,参与维基百科的词条:普里姆算法 将上述点与点关系以及两点之间距离(边长,有的文献
-
设T=(V,E)是一棵顶点和边的树,代价已知。我们想构造一个最小权完备图G=(V,E'),它的唯一最小生成树是T。 示例:考虑下面的树T,红色边具有给定的代价。将添加虚线边以从这棵树构造一个完整的图。 作为其唯一MST而跨越T的最小权完备图G如下所示: 2)对MST的所有其他边,权重,按权重递减的顺序重复。进行只包括而不包括其他MST边的切割。此切割的任何未知非MST边的权重应为。 问题: 1)上

