寻找跨越给定最小生成树的最小权完备图

Question

设T=(V，E)是一棵V顶点和E=V-1边的树，代价已知。我们想构造一个最小权完备图G=(V,E')，它的唯一最小生成树是T。

示例：考虑下面的树T，红色边具有给定的代价。将添加虚线边以从这棵树构造一个完整的图。

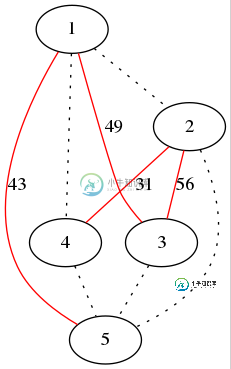
作为其唯一MST而跨越T的最小权完备图G如下所示：

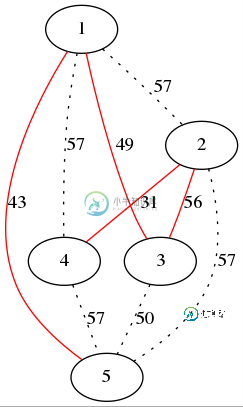
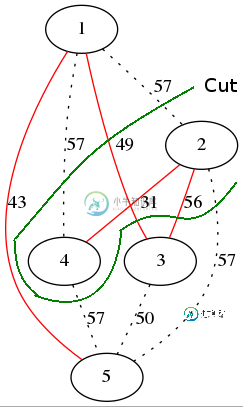
2）对MST的所有其他边E_i，权重W_i，按权重递减的顺序重复。进行只包括E_i而不包括其他MST边的切割。此切割的任何未知非MST边的权重应为W_i+1。

问题：

1）上述算法正确吗？根据割的性质，应该正确。

1）使用并查找，通过代价递增迭代所有MST边，统一同一分量下的对应顶点。

2）在每一步中，两个不同的组件通过成本w的边统一起来。在同一（新）组件内形成循环的任何其他边的成本都应该为w+1。

Answer 1

回答我自己的问题

下面是我想出的一个有效的答案，也是根据@Sasha的反馈。假设我们想计算完全图G的总权，即；

设T=(V,E）是由V个顶点和E=V-1条边组成的树，且权值已知。计算最小权重完全图G=(V,E')的总权W_total，该图跨越T作为其唯一的最小生成树。注意：边缘权重是自然数。

null

for all vertices v1 in set1
  for all vertices v2 in set2
    create edge e = (v1, v2); ignore if edge is the MST edge
    w_e = w_mst_edge + 1

所以运行时间变成O(E+V*logV)=O(V^2)，因为在完全图G中我们有E=V*(V-1)/2条边。