给出边的最小置换权重，使给定的边集为最小生成树

Question

问题:

给定 N 个节点和 M 条边的图形，边的索引范围为 1 -

你需要为M条边分配权重。权重在[1...M]，并且每个数字只能出现一次。

简而言之，答案应该是[1]的置换数组...M]，其中arr[i] = x表示edge[i]的权重为x。

你得到了一个由n-1条边组成的集合。R保证是图的生成树。

找到一种分配权重的方法，使R是图的最小生成树，如果有多个答案，则打印具有最小字典顺序的答案。

约束条件:

N, M <= 10^6

例子：

边缘:

3 4
1 2
2 3
1 3
1 4

R = [2, 4, 5]

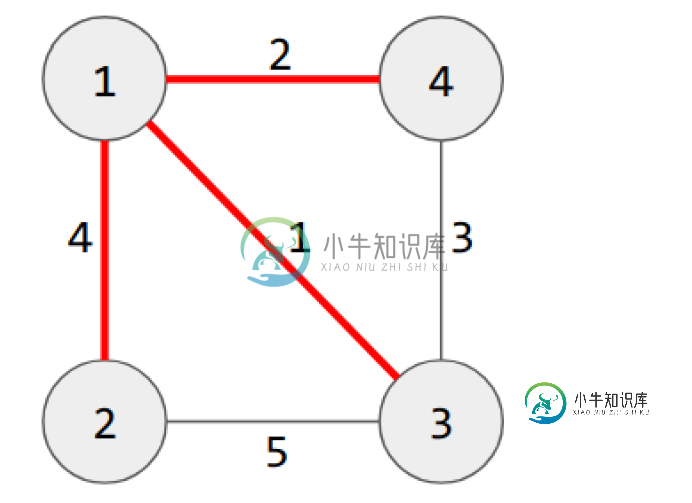
Answer: 3 4 5 1 2

说明：

如果像上图一样给图赋权，那么MST就是集合R，它的字典序最小。

我对O（N^2）的看法：

因为它要求最小的字典顺序，所以我遍历边的列表，以递增的顺序分配权重。最初，w = 1。可能有三种情况:

< li >如果edge[i]为R，则分配权重[i] = w，w增加1 < li >如果边[i]不在R中:假设边[i]连接节点u和v。为R中从u到v的路径中的每条边分配权重并增加w(如果该边尚未分配)。然后为edge[i]指定权重并增加w < li >如果指定了edge[i],请跳过它

有什么方法可以改进我的解决方案，使其可以在O(N.logN)或更少的时间内工作？

Answer 1

是的，有一个O（m）对数m）时间算法。

非树边e的基本循环由e和eendpoint之间的树中路径组成。给定权重，生成树是最小的当且仅当对于每个非树边e，e的基本循环中最重的边是e本身。

词典编纂目标适合于贪婪算法，其中我们找到边缘1的最无效赋值，然后边缘2给定边缘1，然后边缘3给定先前边缘，依此类推。这是核心思想：如果下一个未分配的边是非树边，则在其基本循环中将下一个数字分配给未分配的树边;，然后分配下一个数字。

在此示例中，边 3-4 是第一个，边 1-3 和 1-4 完成其基本周期。因此，我们分配 1-3 → 1 和 1-4 → 2，然后 3-4 → 3。接下来是1-2，一个树边，所以1-2→4。最后，2-3 → 5（已经分配了 1-2 和 1-3）。

为了有效地实现这一点，我们需要两个要素：一个是枚举基本循环中未赋值的边的方法，另一个是赋值的方法。我对前者的建议是存储具有收缩指定边的生成树。我们不需要任何花哨的东西；首先在某处建立生成树并运行深度优先搜索来记录父指针和深度。e的基本循环将由eendpoint的最小公共祖先的路径给出。为了进行收缩，我们添加一个布尔字段，指示父边是否收缩，然后使用不相交集合林中的路径压缩技巧。工作将是O（m log m）最坏情况，但O（m）平均情况。我认为很有可能在这里插入离线最不常见的祖先算法，从而将最坏情况降到O（m）。

至于数字分配，我们可以在线性时间内处理。对于每条边，记录导致其被指定的边的索引。最后，稳定地按此索引进行bucket排序，通过将树边缘放在非树之前来打破关系。这可以在O（m）时间内完成。