在图中找到生成树的数量
问题陈述
在下图中找到生成树的数量。
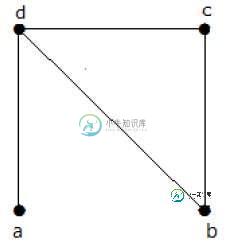
解决方案
从上图获得的生成树的数量为3。它们如下-
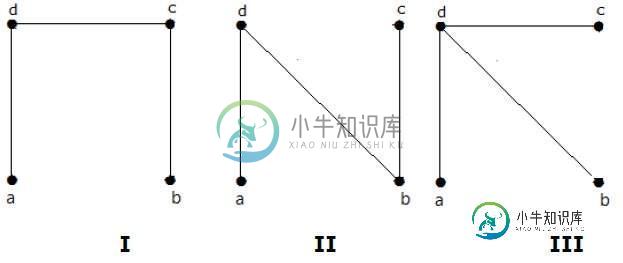
这三个是给定图的生成树。在此,图I和图II是同构的。显然,非同构生成树的数量为2。
-
假设我选择V(H)={a,e,f}和e(H)={ae,af,fe} 现在,对于每条边e∈e(H),我们用e'记下了(来自原始图G的) 达到这个最小值的边。所以E'={bc,df,eg},因为bc=4,df=9,eg=8,是连接我的元件的最小边。我在H中有一个相对于代价函数C′的最小生成树,而a′是这棵树的边集。 但是我的A'的边和E'的没有一条是一样的。
-
假定给定一个给定图G(有n个顶点和m条边)的最小生成树T和一个新边e=(u,v),它的权重为w。 (I)检验T是否为MST;(II)如果不是,给出了求图G+E的最小生成树的有效算法。
-
null 所有权重都将为正值。 我们还可以假设没有权重在图中出现超过三次。 顶点数将小于或等于40,000。 边数将小于或等于100,000。 在顶点权重不同的图中只有一棵最小生成树。我认为找到最小生成树数目的最好方法一定是使用这个属性。 编辑: 现在考虑一个使用Kruskal算法的部分形成的生成树。我们已经插入了一些长度小于N的边,现在必须选择几条长度为N的边。算法规定,如果可能的话,我们必须在
-
我正试图从一个加权无向图中找到跨越三的次优最小值。我知道如何使用Kruskal算法计算MST,我想用这种方法找到第二好的最小算法: 步骤: > 对所有图形边进行排序。 使用Kruskal计算MST 从不在第一个MST中的图中获取最小权重边,并将其添加到MST中(现在MST有一个循环) 在新形成的循环中移除最大重量边 这应该是第二好的MST吧? 顺便说一句,我知道这里有一个主题,指出了一个算法,它在
-
我一直在读生成树的概念及其类型。这就是我所理解的: 生成树:图G中连接所有顶点的边数最小的子集 最小生成树:它是边权的总和最小的生成树。 现在,这是否意味着,在检索MST时, > 如果我们遇到G中的一条路径,它有更多的边(与其他路径相比),但在边权重总和上的权重最小(与所有其他路径相比),我们将不把它视为MST? MST的概念是否只有在G有多个生成树的情况下才起作用?其他跨树=mst? 谢谢你的帮
-
开始使用AWS代码构建。 目标是让docker图像作为最终结果,并在其中运行nodejs、hapi和示例应用程序。 目前我有一个问题:“无法准备上下文:无法在Dockerfile路径中计算符号链接: lstat /tmp/src049302811/src/Dockerfile:没有这样的文件或目录”出现在BUILD阶段。 项目详情: S3存储桶用作源 存储在各自S3存储桶中的ZIP文件包含buil

