为什么在将乘法的强度减少到循环携带加法之后，此代码执行得更慢？

Question

我正在阅读Agner Fog的优化手册——我遇到了这个例子：

double data[LEN];

void compute()
{
    const double A = 1.1, B = 2.2, C = 3.3;

    int i;
    for(i=0; i<LEN; i++) {
        data[i] = A*i*i + B*i + C;
    }
}

Agner指出，有一种方法可以优化此代码—通过认识到循环可以避免使用代价高昂的乘法，而是使用每次迭代应用的“增量”。

我用一张纸来证实理论，首先...

...当然，他是对的——在每次循环迭代中，我们可以通过添加“增量”来基于旧结果计算新结果。这个增量从值“A B”开始，然后在每一步上递增“2*A”。

因此，我们将代码更新为如下所示：

void compute()
{
    const double A = 1.1, B = 2.2, C = 3.3;
    const double A2 = A+A;
    double Z = A+B;
    double Y = C;

    int i;
    for(i=0; i<LEN; i++) {
        data[i] = Y;
        Y += Z;
        Z += A2;
    }
}

就操作复杂性而言，这两个版本的函数的差异确实是惊人的。与加法相比，乘法在我们的CPU中以显着慢而闻名。我们已经替换了3次乘法和2次加法......只有2次加法！

因此，我继续添加一个循环来执行多次计算，然后保持执行所需的最短时间：

    unsigned long long ts2ns(const struct timespec *ts)
    {
        return ts->tv_sec * 1e9 + ts->tv_nsec;
    }

    int main(int argc, char *argv[])
    {
        unsigned long long mini = 1e9;
        for(int i=0; i<1000; i++) {
            struct timespec t1, t2;
            clock_gettime(CLOCK_MONOTONIC_RAW, &t1);
            compute();
            clock_gettime(CLOCK_MONOTONIC_RAW, &t2);
            unsigned long long diff = ts2ns(&t2) - ts2ns(&t1);
            if (mini > diff) mini = diff;
        }
        printf("[-] Took: %lld ns.\n", mini);
    }

我编译这两个版本，运行它们。。。看看这个：

# gcc -O3 -o 1 ./code1.c

# gcc -O3 -o 2 ./code2.c

# ./1
[-] Took: 405858 ns.

# ./2
[-] Took: 791652 ns.

嗯，这是出乎意料的。因为我们报告了最短的执行时间，所以我们正在丢弃操作系统各个部分造成的“噪音”。我们还注意在一台完全不起任何作用的机器上运行。结果或多或少是可重复的-重新运行这两个二进制文件表明这是一个一致的结果：

# for i in {1..10} ; do ./1 ; done
[-] Took: 406886 ns.
[-] Took: 413798 ns.
[-] Took: 405856 ns.
[-] Took: 405848 ns.
[-] Took: 406839 ns.
[-] Took: 405841 ns.
[-] Took: 405853 ns.
[-] Took: 405844 ns.
[-] Took: 405837 ns.
[-] Took: 406854 ns.

# for i in {1..10} ; do ./2 ; done
[-] Took: 791797 ns.
[-] Took: 791643 ns.
[-] Took: 791640 ns.
[-] Took: 791636 ns.
[-] Took: 791631 ns.
[-] Took: 791642 ns.
[-] Took: 791642 ns.
[-] Took: 791640 ns.
[-] Took: 791647 ns.
[-] Took: 791639 ns.

接下来要做的唯一一件事是查看编译器为这两个版本中的每一个创建了什么类型的代码。

Objump-d-S显示compute的第一个版本-“哑”但不知何故快速的代码-有一个如下所示的循环：

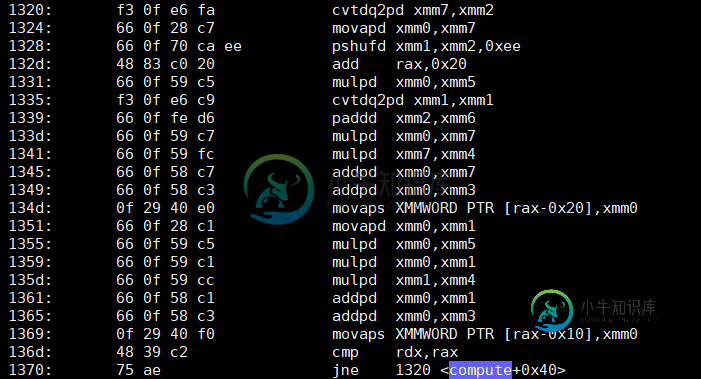
那么第二个优化版本呢？它只做了两个附加功能？

现在我不知道你的情况——但就我自己而言，我是......困惑。第二个版本的指令大约少了4倍——其中两个主要的指令只是两个基于SSE的添加（addsd）。第一个版本，不仅有4倍的指令......它还充满了（如预期的）乘法（mulpd）。

我承认我没想到会有这样的结果。

并不是因为我是阿格纳的粉丝（我是，但这无关紧要）。

知道我错过了什么吗？我在这里犯了什么错误，这可以解释速度上的差异吗？请注意，我已经在Xeon W5580和Xeon E5 1620上进行了测试-在这两个版本中，第一个（哑）版本比第二个版本快得多。

编辑：为了便于再现结果，我在两个版本的代码中添加了两个giist：Dumb但不知何故更快和优化，但不知何故更慢。

P、 请不要评论浮点精度问题；这不是这个问题的重点。

Answer 1

如果您需要此代码快速运行，或者您很好奇，您可以尝试以下操作：

您将a[i]=f（i）的计算更改为两个加法。修改此选项以使用两个加法计算a[4i]=f（4i），使用两个加法计算a[4i 1]=f（4i 1），依此类推。现在有四个可以并行进行的计算。

编译器很有可能会执行相同的循环展开和向量化，并且您有相同的延迟，但对于四个操作，而不是一个操作。

Answer 2

这里的主要区别是循环依赖。第二种情况下的循环是依赖的——循环中的操作取决于上一次迭代。这意味着每次迭代甚至不能开始，直到上一次迭代完成。在第一种情况下，循环主体是完全独立的——循环主体中的所有内容都是自包含的，仅取决于迭代计数器和常量值。这意味着循环可以并行计算——多次迭代都可以同时工作。这允许循环被简单地展开和矢量化，重叠许多指令。

如果您查看性能计数器（例如使用perf stat./1），您会看到第一个循环除了运行得更快之外，每个循环还运行更多的指令（IPC）。相比之下，第二个循环有更多的依赖周期——CPU无所事事，等待指令完成，然后才能发出更多指令的时间。

第一个问题可能会导致内存带宽瓶颈，特别是如果您让编译器在Sandybridge上使用AVX自动向量化（gcc-O3-march=native），如果它能够使用256位向量。此时IPC将下降，尤其是对于对于三级缓存来说太大的输出阵列。

需要注意的是，展开和向量化不需要独立的循环——您可以在存在（一些）循环依赖项时执行它们。但是，这更难，回报也更少。因此，如果您想看到矢量化的最大加速，尽可能删除循环依赖项会有所帮助。

Answer 3

理解性能差异的关键在于矢量化。是的，基于加法的解决方案在其内部循环中只有两条指令，但重要的区别不在于循环中有多少条指令，而在于每条指令执行的工作量。

在第一个版本中，输出完全依赖于输入：每个数据本身都是一个函数，这意味着每个数据都可以按任意顺序计算：编译器可以向前、向后、侧向，无论什么，你仍然会得到相同的结果，除非你从另一个线程观察到内存，你永远不会注意到数据是以何种方式处理的。

在第二个版本中，输出不依赖于i，它依赖于循环最后一次的A和Z。

如果我们将这些循环体表示为小的数学函数，它们的整体形式会非常不同：

• f（i）-

在后一种形式中，对i没有实际的依赖关系-您可以计算函数值的唯一方法是通过知道上一个Y和Z从最后一次调用函数，这意味着函数形成一个链-在完成前一个之前您不能执行下一个。

为什么这很重要？因为CPU有向量并行指令，每个指令都可以同时执行四个算术运算！（AVX CPU可以并行执行更多操作。）那就是四次乘法、四次加法、四次减法、四次比较——四个什么都可以！所以如果你试图计算的输出只依赖于输入，那么你可以安全地一次做四个——不管它们是前进还是后退，因为结果是一样的。但是如果输出依赖于以前的计算，那么你就只能以串行形式进行——一次一个。

这就是为什么“更长”的代码在性能上胜出。即使它有更多的设置，并且它实际上做了更多的工作，但大部分工作是并行完成的：它不只是在循环的每次迭代中计算data[i]-它同时计算data[i]、data[i 1]、data[i 2]和data[i 3]，然后跳转到下一组四个。

为了扩展我在这里的意思，编译器首先将原始代码转换为这样的内容：

int i;
for (i = 0; i < LEN; i += 4) {
    data[i+0] = A*(i+0)*(i+0) + B*(i+0) + C;
    data[i+1] = A*(i+1)*(i+1) + B*(i+1) + C;
    data[i+2] = A*(i+2)*(i+2) + B*(i+2) + C;
    data[i+3] = A*(i+3)*(i+3) + B*(i+3) + C;
}

你可以说服自己，如果你眯着眼睛看的话，你会做和原来一样的事情。它之所以做到这一点，是因为所有这些相同的运算符垂直线：所有这些操作都是相同的操作，只是在不同的数据上执行，CPU有特殊的内置指令，可以在每个时钟周期内对不同的数据同时执行四个或四个操作。

请注意快速解决方案中说明中的字母p和慢速解决方案中说明中的字母s。这是“加法压缩双精度”和“乘法压缩双精度”，而不是“加法单精度”

不仅如此，编译器似乎也部分展开了循环-循环不仅在每次迭代中执行四个值，实际上还执行八个值，并交错操作以避免依赖项和暂停，从而减少了汇编代码必须测试的次数

然而，所有这些都只在循环迭代之间没有依赖关系的情况下才起作用：如果唯一确定每个数据发生什么的事情是它本身。如果存在依赖关系，如果上一次迭代的数据影响下一次迭代，那么编译器可能会受到这些依赖关系的约束，根本无法更改代码-而不是编译器能够使用奇特的并行指令或巧妙的优化（CSE、强度缩减、循环展开、重新排序等），您得到的代码正是您所输入的代码-添加Y，然后添加Z，然后重复。

但是在这里，在第一个版本的代码中，编译器正确地认识到数据中没有依赖项，并且发现它可以并行地完成工作，所以它做到了，这就是所有区别所在。