二叉搜索树中的删除操作:继任者或前任
删除操作是二叉搜索树中最复杂的操作,因为它需要考虑几种可能性:
- 删除的节点是叶节点
- 删除的节点只有一个子节点
- 删除的节点同时具有左子节点和右子节点
前两种情况很简单。但是对于第二个,我读了很多书或文档,解决方案是:在正确的子树中找到最小值并将其替换为已删除的节点。然后从右侧子树中删除它。
我可以完全理解这个解决方案。
事实上,一般情况下,右边子树中最小值的节点称为该节点的后继节点。所以上面的解决方案是用后继节点的值替换被删除的节点。并从子树中删除后继节点。
另一方面,每个节点的前身是左子树中具有最大值的节点。
我认为,用其前身替换已删除的节点也应该有效。
比如《C语言中的数据结构和算法分析》一书中使用的例子。
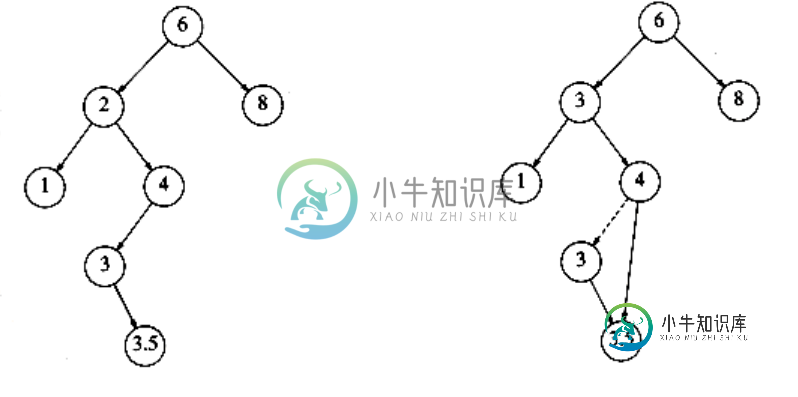
如果我们想删除节点“2”。然后我们用“2”的后继者“3”替换它。
我想,用“2”的前身“1”代替“2”也可以。正确但是书上一点也没有提到它。
那么这里有什么约定吗?如果在一次删除操作后,有两个结果都是正确的。如何保持一致?
编辑:
根据有关此问题的新知识更新某些内容。事实上,《c中的数据结构和算法分析》一书就讨论了这个问题。总之,它如下:
- 首先,两种方法(基于继任者或前任者)都应该有效
- 如果重复O(n^2),则在树上插入/删除对。所有的删除操作都基于后续操作。然后,树将变得不平衡。因为该算法使左子树比右子树更深。这个想法可以用以下两张图片来说明:


然后介绍了平衡搜索树的概念,如AVL树。
共有1个答案
我可以说这个理论,对我来说,你的论点似乎是正确的,一个人可以采取前任或继任者。
现在在实践中,我认为最好的决定是保持树的平衡,并根据哪个深度最低在两个选项之间切换。
-
在二元搜索树的情况下,为什么我们不能简单地在一个节点有两个子节点的情况下,将一个节点的前一个节点替换为后一个节点?
-
我正在尝试为我一直在研究的BST结构实现一个移除方法。以下是包含查找、插入和删除方法的代码: 我被告知可以使用insert方法来帮助我使用remove方法,但我只是不知道如何获取最小/最大的元素,然后用该值替换我正在删除的元素,然后递归地删除我获取替换值的节点,同时仍然保持O(logn)的复杂性。有人有什么想法或明显的漏洞我错过了,或任何其他有帮助的,因为我撞我的头在这个问题上? 编辑:我用答案的
-
我在做作业,实现自己的二叉查找树。问题是,我们有自己的节点实现,它的父节点是不可直接访问的。 我一直在寻找答案,但我不想完全照搬解决方案,尽管如此,我似乎仍然没有得到正确的答案。我错过了一些元素没有被删除的情况。 你能帮帮我吗?我做错了什么? 这是删除方法: 节点使用通用接口 只有比较的方法。它看起来像这样 我在remove中使用了另一种方法,它设置节点的父节点的子节点,具体取决于它的左子节点还是
-
这里是我试图实现的BST,但是remove方法不会删除具有给定值的节点。我试着这样做: 首先检查当前节点(我要删除的节点)是否有正确的子节点。 1.2.1)如果右子节点有一个左子节点,则我将当前节点替换为最小节点,该最小节点大于当前节点,并替换为右子树中最左侧的节点 1.2.2)如果没有,我就用它的正确子节点替换当前节点,但是代码没有删除选中的节点,哪里出错了?
-
首先,这是家庭作业,所以把它放在外面。 我应该用特定的方法实现二叉查找树: void insert(字符串)、boolean remove(字符串)和boolean find(字符串)。 我已经能够成功地编程和测试插入,并找到方法,但我有困难与删除。 我的程序中发生的事情是,删除实际上并没有从树中删除任何东西,我相信这是因为它只引用当前节点的本地创建,但我可能错了。我认为我可以实现我需要测试的不同
-
我试图通过这个链接BinarySearchTree来理解BST。但我在其他部分感到困惑 我不能理解其他部分,其中左大部分节点的右子树被找到,然后分配到该节点。但在这里,该节点都不为空,并且返回右节点,这对我来说是没有意义的。我希望这是一个正确的实现。有人能帮我了解一下这里发生了什么吗。

