第十五课 相机控制(二)
在这一节中我们将使用鼠标来控制相机的方向,从而得我们的相机控制更加完善。相机根据其使用的场景不同而有不同的自由度。在本教程中我们将要实现的是与第一人称游戏中相似的相机控制(如枪战类游戏)。这意味着我们将可以使相机完成 360 度的旋转(绕着 Y 轴),这与我们的头部向左转向右转、身体转一整圈类似。除此之外我们也能使相机向上或者向下倾斜以获得更好的向上的或者向下的视野但是我们不能使之沿同一转向翘起一个完整的圆或者像飞机倾斜转身那样盘旋出一个圈。这种自由度一般被使用在飞行模拟器中,但是无论如何,通过对相机控制的完善,会让我们在后面的学习中能够更方便的探寻三维世界。
下面这副世界战争二中的防空机枪很好的演示了我们将要构建的相机:

这个枪有两个控制轴:
- 它能够绕向量(0,1,0)进行360度旋转,这个角度被称作水平角,而这个向量被称作纵轴;
- 它能够绕着一个平行于地面的轴向上或者向下旋转,这个动作是受限的,它并不能完整地旋转一整个圆,这个角度被称作俯仰角,而这个这个轴被称作水平轴。需要注意的是纵轴是保持不变的(一直是(0,1,0)),而水平轴则会随着枪进行旋转,并且一直与枪的目标向量垂直,这是获得正确计算公式的关键一点。
我们计划的是让相机随着鼠标的运动而运动,当我们鼠标左右移动时会改变水平角,而当鼠标上下移动时则会改变俯仰角。通过这两个角度我们希望能够计算出相机的目标向量和 up 向量。
使目标向量沿纵轴旋转的方法很简单,使用最基本的三角法则我们会发现目标向量的 Z 分量是水平角向量的 sin 值,而 X 分量则是水平角向量的 cos 值(在这个阶段相机只是简单的直接朝向前方,所以其 Y 分量为0)。大家可以重温第七节中的示意图来理解这一点。
使目标向量绕水平轴旋转则会复杂的多,因为水平轴会随着相机旋转,虽然水平轴可以通过纵轴和经过水平角旋转之后的目标向量的叉乘求出,但是沿着一个未知向量进行旋转(将枪上下移动)还是十分棘手的。
幸运的是我们有一个十分有用的数学工具——四元数来解决这个问题,四元数在 1843 年被爱尔兰数学家 Willilam Rowan Hamilton 发明出来,它是基于复数的,一个四元数 ‘Q’ 可以按下面的方式来定义:

上面等式中的 i、j、k 都是复数,并且它们满足下面的等式:

在实际使用中,我们将四元数定义成一个四维向量,四元数 ‘Q’ 的共轭四元数我们定义成如下形式:

四元数的规范化与向量的规范化一样,接下来我们来介绍如何通过四元数来实现将一个向量绕任意向量进行旋转。关于这些步骤的数学证明,你可以在网上找到更多细节。
一般情况下,计算一个将向量 ‘V’ 旋转 a 角度后的四元数 ‘W’ 可以用下面的方法:

上面的 ‘Q’ 是一个旋转四元数,它可以按照如下方式定义:

在计算出 ‘W’ 之后,我们就能直接得到旋转之后的向量为(W.x,W.y,W.z)。在计算四元数 ‘W’ 的过程中我们需要注意的是:首先我们需要将 ‘Q’ 乘上 ‘V’ ,这个是四元数与向量相乘,其结果是一个四元数,之后我们需要进行一个四元数之间的运算( Q * V 的结果与 'Q' 的共轭四元数相乘)。这两种乘法运算的类型并不相同,在 math_3d.cpp 文件中包含了这些乘法运算的具体实现。
当用户在屏幕中移动鼠标的时候我们需要不断地更新水平角和俯仰角,并且我们需要决定如何初始化这些值。最合理的方式是我们使用提供给相机构造函数的目标向量的来初始化他们。接下来让我们从水平角开始,首先我们从上俯视 XZ 平面得到下图:
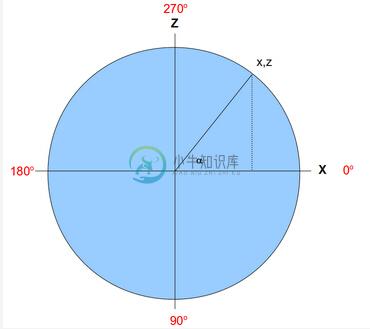
图中目标向量为(x,z),我们想找出由图中 α 表示的水平角度( Y 分量只与俯仰角有关)。由于图中圆的半径为1,所以我们很容易就能看出 α 角的 sin 值就正好为 z,所以计算 z 的 arcsin 值就能获得 α 角度的大小。我们现在就完成了么?当然没有,因为 z 的范围是[-1,1],所以计算得到的 α 角度的范围为[-90°,90°],但是实际上水平角的范围是 360 度。除此之外我们的四元数进行的是顺时针旋转,这意味着当我们使用四元数旋转 90 度时,旋转之后向量与 Z 轴负方向重合并且其 sin 值为 -1,但这刚好与 90 度的 sin 值相反(sin90 = 1)。最简单的解决办法,就是我们只计算 z 的绝对值的 arcsin 值,之后将结果与向量所在的位置的四分之一圆相结合得出最终结果。例如,当我们的目标向量为(0,1)时,我们计算出 1 的arcsin值为 90 度,之后我们从 360 度中减去它,结果为 270度,[0,1]范围之间的 arcsin 值对应[0,90]度之间的角度,结合这个计算出来的角度以及已经确定的向量所处的四分之一圆,我们就能得到最终的水平角。
计算俯仰角则比较简单,我们将俯仰角的范围限定在 -90 度(等于270度——向上看)到 +90 度之间(向下看)。这意味着我们只需要计算 target 向量的 y 分量的 asin 值,然后取反,例如 Y = 1 时 asin 值为 90 度,取反 -90 度,此时看向上,Y = -1,为 -90 度,取反,90度,此时看向下
代码
[cpp] view plaincopy
(camera.cpp:38)
Camera::Camera(int WindowWidth, int WindowHeight, const Vector3f& Pos, const Vector3f& Target, const Vector3f& Up)
{
m_windowWidth = WindowWidth;
m_windowHeight = WindowHeight;
m_pos = Pos;
m_target = Target;
m_target.Normalize();
m_up = Up;
m_up.Normalize();
Init();
} Camera的构造函数现在需要传入的窗口尺寸作为参数,这是因为我们需要将鼠标移动到屏幕的中心点。此外,注意 Init() 函数的调用,它完成了 camera 内部属性的设置。
[cpp] view plaincopy
(camera.cpp:54)
void Camera::Init()
{
Vector3f HTarget(m_target.x, 0.0, m_target.z);
HTarget.Normalize();
if (HTarget.z >= 0.0f)
{
if (HTarget.x >= 0.0f)
{
m_AngleH = 360.0f - ToDegree(asin(HTarget.z));
}
else
{
m_AngleH = 180.0f + ToDegree(asin(HTarget.z));
}
}
else
{
if (HTarget.x >= 0.0f)
{
m_AngleH = ToDegree(asin(-HTarget.z));
}
else
{
m_AngleH = 90.0f + ToDegree(asin(-HTarget.z));
}
}
m_AngleV = -ToDegree(asin(m_target.y));
m_OnUpperEdge = false;
m_OnLowerEdge = false;
m_OnLeftEdge = false;
m_OnRightEdge = false;
m_mousePos.x = m_windowWidth / 2;
m_mousePos.y = m_windowHeight / 2;
glutWarpPointer(m_mousePos.x, m_mousePos.y);
} 在 Init() 函数中我们从计算水平角开始,我们新创建一个目标向量 HTarget(水平目标)——真实目标向量在 XZ 平面上的投影。之后我们对其进行规范化(我们在之前的推导过程中就假设其是在 XZ 平面上的一个单位向量)。接下来,我们会检测 target 向量在哪一个1/4圆里,并利用 z 分量的绝对值计算得到最后的水平角。接下来,我们计算俯仰角,这简单多了。
在 camera 类中我们新增了四个标记变量来表示鼠标是否处于屏幕的某一个边界上面,当我们鼠标处于某一个边界时,相机会自动朝着那个对应的方向转动,这使得我们能够进行 360 度的旋转。我们将这个四个标记变量都初始化为 FALSE,这是因为鼠标最开始是位于屏幕中心的。接下来的两行代码用于计算屏幕的中心坐标(基于屏幕的尺寸),而 glutWarpPointer 函数则用于移动鼠标。
[cpp] view plaincopy
(camera.cpp:140)
void Camera::OnMouse(int x, int y)
{
const int DeltaX = x - m_mousePos.x;
const int DeltaY = y - m_mousePos.y;
m_mousePos.x = x;
m_mousePos.y = y;
m_AngleH += (float)DeltaX / 20.0f;
m_AngleV += (float)DeltaY / 20.0f;
if (DeltaX == 0) {
if (x <= MARGIN) {
m_OnLeftEdge = true;
}
else if (x >= (m_windowWidth - MARGIN)) {
m_OnRightEdge = true;
}
}
else {
m_OnLeftEdge = false;
m_OnRightEdge = false;
}
if (DeltaY == 0) {
if (y <= MARGIN) {
m_OnUpperEdge = true;
}
else if (y >= (m_windowHeight - MARGIN)) {
m_OnLowerEdge = true;
}
}
else {
m_OnUpperEdge = false;
m_OnLowerEdge = false;
}
Update();
} 这个函数用来将鼠标的移动情况传递给相机,传入的参数 x,y 是鼠标在屏幕上的位置,delta 是当前鼠标位置和上次鼠标位置的差,我们分别计算 x 和 y 方向的 delta,计算完后,我们会把当前的鼠标位置保存在 m_mousePos 变量中以便下次调用。接下来,我们使用缩放之后的 delta 值来更新相机的水平角和俯仰角,这里我们使用的缩放因子对于我的电脑是刚好合适的,但是对于不同的电脑可能会需要不同的缩放因子,在后面的教程中当我们会使用帧速作为一个缩放因子。
之后我们根据鼠标的位置来更新 'm_On*Edge' 标记,当鼠标位于某一个边缘时(边缘的默认范围为 10 像素),它就会触发我们的边缘动作。最后,我们调用 Update() 函数基于水平角和俯仰角来重新计算目标向量和up向量。
[cpp] view plaincopy
(camera.cpp:183)
void Camera::OnRender()
{
bool ShouldUpdate = false;
if (m_OnLeftEdge) {
m_AngleH -= 0.1f;
ShouldUpdate = true;
}
else if (m_OnRightEdge) {
m_AngleH += 0.1f;
ShouldUpdate = true;
}
if (m_OnUpperEdge) {
if (m_AngleV > -90.0f) {
m_AngleV -= 0.1f;
ShouldUpdate = true;
}
}
else if (m_OnLowerEdge) {
if (m_AngleV < 90.0f) {
m_AngleV += 0.1f;
ShouldUpdate = true;
}
}
if (ShouldUpdate) {
Update();
}
} 这个函数在主函数的渲染循环中被调用,我们需要在鼠标位于屏幕的某一个边缘并且不再移动时使用这个函数,在这种情况下,并没有鼠标事件发生但是我们却希望相机继续移动(直到鼠标离开边缘)。我们检查是否某一个标记变量被设置为 true,并且更新对应的角度。而当鼠标离开窗口的时候我们在鼠标事件处理中会监听到这一事件并且将标记变量置为 false。注意俯仰角的角度是限定在 -90 到 +90 之间的,这是为了防止我们向上或者向下旋转一整圈。
[cpp] view plaincopy
(camera.cpp:214)
void Camera::Update()
{
const Vector3f Vaxis(0.0f, 1.0f, 0.0f);
// Rotate the view vector by the horizontal angle around the vertical axis
Vector3f View(1.0f, 0.0f, 0.0f);
View.Rotate(m_AngleH, Vaxis);
View.Normalize();
// Rotate the view vector by the vertical angle around the horizontal axis
Vector3f Haxis = Vaxis.Cross(View);
Haxis.Normalize();
View.Rotate(m_AngleV, Haxis);
View.Normalize();
m_target = View;
m_target.Normalize();
m_up = m_target.Cross(Haxis);
m_up.Normalize();
} 这个函数根据水平角和俯仰角更新 target 和 up 向量。在开始之前我们就将 view 向量重置,这表示这个 view 向量平行于地面(俯仰角为0),并且指向右方(水平角为0)。我们将纵轴设置为竖直的指向上方,通过水平角使 view 向量绕纵轴旋转,由此得到结果总是大致指向要观察的物体,但摄像机指向的高度却不一定正确(比如位于 XZ 平面上),我们通过使用垂直轴和 view 向量做一个叉积,得到一个位于 XZ 平面上并且与 view 向量与纵轴所组成的平面垂直的向量,而这就是我们新的水平轴,现在我们就可以根据俯仰角使 view 向量绕着水平轴进行旋转了,这样最终得到的 view 向量就是我们的目标向量了。之后我们只要将其设置到相应的相机参数中即可。最后我们还要修正 up 向量,例如当相机向上翘起,那么 up 向量也需要向后翘起( up 向量必须与目标向量成 90 度)。就像我们抬头看天空时候,我们的头必须向后仰。新的 up 向量我们可以通过最终得到的 view 向量和新的水平轴叉乘得到。如果俯仰角仍旧为 0,那么目标向量还是会处于 XZ 平面上,并且 up 向量也仍旧是(0,1,0)。如果目标向量向上或者向下翘,那么 up 向量也会相应的向后或者向前。
(tutorial15.cpp:209)
glutGameModeString("1920x1200@32");
glutEnterGameMode();这个 glut 函数使得我们能够在被称作的高性能模式“游戏模式”下进行全屏运行,这使得相机旋转 360 度变得更加容易,因为我们所需要做的仅仅就是将鼠标移动到屏幕边缘即可。注意:分辨率和像素格式都是通过这个字符串定义的,每个像素32位提供了渲染时的最大颜色值。
(tutorial15.cpp:214)
pGameCamera = new Camera(WINDOW_WIDTH, WINDOW_HEIGHT);我们在此动态的创建一个相机对象,这是因为它要执行一个 glut 函数(glutWarpPointer),如果 glut 没有进行初始化,则此调用会失败。
(tutorial15.cpp:99)
glutPassiveMotionFunc(PassiveMouseCB);
glutKeyboardFunc(KeyboardCB);在这里我们注册了两个 glut 回调函数,其中一个是为了捕捉鼠标事件,另一个则是为了常规的键盘按键捕捉(特殊按键回调函数用于捕捉方向键以及功能键事件)。Passive 运动表示鼠标只是进行移动而没有任何按键事件发生。
[cpp] view plaincopy
(tutorial15.cpp:81)
static void KeyboardCB(unsigned char Key, int x, int y)
{
switch (Key) {
case 'q':
exit(0);
}
}
static void PassiveMouseCB(int x, int y)
{
pGameCamera->OnMouse(x, y);
} 现在我们使用全屏模式,退出程序则变得比较困难了。按键回调函数会捕捉 ‘q’ 键的按下事件并使的程序退出,鼠标回调函数则仅仅是将鼠标位置传递给相机。
(tutorial15.cpp:44)
static void RenderSceneCB()
{
pGameCamera->OnRender();无论何时,我们进入主循环的时候必须通知相机,这使得我们的相机能够在鼠标处于屏幕边缘并且不移动的时候继续旋转。
操作结果


