Java实现走迷宫回溯算法

以一个M×N的长方阵表示迷宫，0和1分别表示迷宫中的通路和障碍。设计一个程序，对任意设定的迷宫，求出一条从入口到出口的通路，或得出没有通路的结论。

（1） 根据二维数组，输出迷宫的图形。
（2） 探索迷宫的四个方向：RIGHT为向右，DOWN向下，LEFT向左，UP向上，输出从入口到出口的行走路径。

例子：

左上角（1，1）为入口，右下角（8，9）为出口。

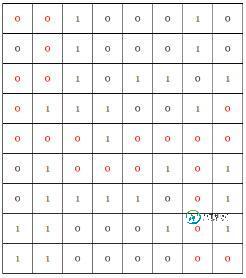
可使用回溯方法，即从入口出发，顺着某一个方向进行探索，若能走通，则继续往前进；否则沿着原路退回，换一个方向继续探索，直至出口位置，求得一条通路。假如所有可能的通路都探索到而未能到达出口，则所设定的迷宫没有通路。

import java.util.*;

class Position{
 public Position(){

 }

 public Position(int row, int col){
  this.col = col;
  this.row = row;
 }

 public String toString(){
  return "(" + row + " ," + col + ")";
 }

 int row;
 int col;
}

class Maze{
 public Maze(){
  maze = new int[15][15];
  stack = new Stack<Position>();
  p = new boolean[15][15];
 }

 /*
  * 构造迷宫
  */
 public void init(){
  Scanner scanner = new Scanner(System.in);
  System.out.println("请输入迷宫的行数");
  row = scanner.nextInt();
  System.out.println("请输入迷宫的列数");
  col = scanner.nextInt();
  System.out.println("请输入" + row + "行" + col + "列的迷宫");
  int temp = 0;
  for(int i = 0; i < row; ++i) {
   for(int j = 0; j < col; ++j) {
    temp = scanner.nextInt();
    maze[i][j] = temp;
    p[i][j] = false;
   }
  }
 }

 /*
  * 回溯迷宫，查看是否有出路
  */
 public void findPath(){
  // 给原始迷宫的周围家一圈围墙
  int temp[][] = new int[row + 2][col + 2];
  for(int i = 0; i < row + 2; ++i) {
   for(int j = 0; j < col + 2; ++j) {
    temp[0][j] = 1;
    temp[row + 1][j] = 1;
    temp[i][0] = temp[i][col + 1] = 1;
   }
  }
  // 将原始迷宫复制到新的迷宫中
  for(int i = 0; i < row; ++i) {
   for(int j = 0; j < col; ++j) {
    temp[i + 1][j + 1] = maze[i][j];
   }
  }
  // 从左上角开始按照顺时针开始查询

  int i = 1;
  int j = 1;
  p[i][j] = true;
  stack.push(new Position(i, j));
  while (!stack.empty() && (!(i == (row) && (j == col)))) {

   if ((temp[i][j + 1] == 0) && (p[i][j + 1] == false)) {
    p[i][j + 1] = true;
    stack.push(new Position(i, j + 1));
    j++;
   } else if ((temp[i + 1][j] == 0) && (p[i + 1][j] == false)) {
    p[i + 1][j] = true;
    stack.push(new Position(i + 1, j));
    i++;
   } else if ((temp[i][j - 1] == 0) && (p[i][j - 1] == false)) {
    p[i][j - 1] = true;
    stack.push(new Position(i, j - 1));
    j--;
   } else if ((temp[i - 1][j] == 0) && (p[i - 1][j] == false)) {
    p[i - 1][j] = true;
    stack.push(new Position(i - 1, j));
    i--;
   } else {
    stack.pop();
    if(stack.empty()){
     break;
    }
    i = stack.peek().row;
    j = stack.peek().col;
   }

  }

  Stack<Position> newPos = new Stack<Position>();
  if (stack.empty()) {
   System.out.println("没有路径");
  } else {
   System.out.println("有路径");
   System.out.println("路径如下：");
   while (!stack.empty()) {
    Position pos = new Position();
    pos = stack.pop();
    newPos.push(pos);
   }
  }

  /*
   * 图形化输出路径
   * */

  String resault[][]=new String[row+1][col+1];
  for(int k=0;k<row;++k){
   for(int t=0;t<col;++t){
    resault[k][t]=(maze[k][t])+"";
   }
  }
  while (!newPos.empty()) {
   Position p1=newPos.pop();
   resault[p1.row-1][p1.col-1]="#";

  }

  for(int k=0;k<row;++k){
   for(int t=0;t<col;++t){
    System.out.print(resault[k][t]+"\t");
   }
   System.out.println();
  }


 }

 int maze[][];
 private int row = 9;
 private int col = 8;
 Stack<Position> stack;
 boolean p[][] = null;
}

class hello{
 public static void main(String[] args){
  Maze demo = new Maze();
  demo.init();
  demo.findPath();
 }
}

运行示例：

请输入迷宫的行数
3
请输入迷宫的列数
3
请输入3行3列的迷宫
0 1 1
0 0 1
1 0 0

有路径
路径如下：

请输入迷宫的行数
9
请输入迷宫的列数
8
请输入9行8列的迷宫
0 0 1 0 0 0 1 0
0 0 1 0 0 0 1 0
0 0 1 0 1 1 0 1
0 1 1 1 0 0 1 0
0 0 0 1 0 0 0 0
0 1 0 0 0 1 0 1
0 1 1 1 1 0 0 1
1 1 0 0 0 1 0 1
1 1 0 0 0 0 0 0

有路径
路径如下：

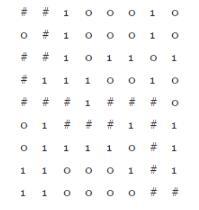
以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。