C++中double浮点数精度丢失的深入分析

看了一篇关于C/C++浮点数的博文，在Win32下，把int, 指针地址,long等4字节整数赋给一个double后，再用该double数赋给原始类型的数，得到的结果于最初的数值一致，即不存在任何精度丢失。例如下面的结果将总是true:

 long a=123456; //assign any long number here
 double db=a;
 long b=db;
 printf("%s\n",a==b?"true":"false");

但是对于long long或win64下的指针地址等8字节整数将存在精度丢失，于是对这方面做了一个简单的测试：

#include<iostream>
#include<stdlib.h>

void showEncodeOfDouble(unsigned char* db){

 const int ByteLength=8; 
 for(int i=ByteLength-1;i>=0;i--) 
  printf(" %.2x",db[i]);

 printf("\n");

}


int main(){
 
 unsigned long long maxULL=0xffffffffffffffff; //2^64-1=18446744073709551615,
             //max unsigned long long
 printf("%llu\n",maxULL);

 double d1=maxULL;        //20bit Significant,Precision Loss 
 printf("%f\n",d1);      

 maxULL=d1;
 printf("%llu\n",maxULL);
 
 showEncodeOfDouble((unsigned char*)&d1);

 system("pause");
 return 0;
}

输出的结果如下（visual studio,win32）：

18446744073709551615
18446744073709552000.000000
9223372036854775808
 43 f0 00 00 00 00 00 00

至此，有两点疑问（暂时不理会代码中showEncodeOfDouble的结果）：

  1）为什么丢失精度后得到的double数是18446744073709552000.000000？
  2）为什么将double数重新转化为unsigned long long后得到的数又和double不一致呢？

对于这两个问题，需要对C++浮点数的规格有一定的了解。

1  IEEE浮点标准

C/C++采用的是IEEE浮点标准，它以“二进制的科学表示法”表示一个小数：

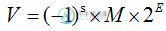
其中M是一个整数部分仅有一位的二进制小数，例如1.011，表示十进制下的1.375。E表示该小数以2为底时的阶数。基于以上的表示方式，小数需要对三部分进行编码：表示符号的s，及阶码E、尾数码M。C++中的double类型三种编码所占的位数如图所示。

53位尾数码所能达到的精度为53二进制位，约为16 个十进制位( 53 log10(2) ≈ 15.955) [1]，尾数码的编码中还有一个隐含的开头整数位1（或0，当11位阶码全0时）因此实际中可得15-17位十进制的精度。当有效位数最多15位的十进制数转换成double然后重新转换为原来的十进制类型时，数值保持一致；另一方面，将一个double数转化为可以容纳17位以上有效数字的十进制数再重新转化为double，结果数值也保持一致。

这就解释了为什么4字节的整数转化为double重新转化能保持一致（2^32=4294967296仅10个有效位），而8字节的整数却可能丢失精度（2^64-1=18446744073709551615共20个有效位）。但第一个问题中整数丢失精度后转化成的double数值是怎么来的呢，这需要了解C++阶码和尾数对于double数值的意义。

2 阶码编码和尾数编码

在阶码编码中，有一个常数偏置量Bias=1023，假设11位阶码所代表的无符号整数值为e，

1）若e不为0（11位全为1时用于表示特殊数字，此处不讨论），则double数值为

2）若e=0，则小数值为

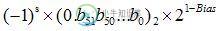
那么，可以看函数showEncodeOfDouble了，它的作用是将一个double数的编码按字节打印出来（左边是高字节），按其打印结果按照上面计算，可知double编码值表示的数值是2^64，这是合理的，当把精度较高的整数转化为double时，C++采用向偶数舍入的方式得到最接近的值[2]。至于打印出的结果，属于C++浮点数打印中的细节问题。

3 C++浮点数打印

许多C/C++的库中在输出double时，通常有意使得输出结果简短些（即使设置了足够多的可见位数），以避免较大位数的输出。直接使用C中的printf或cout打印double数时，打印显示的结果也有可能是带有精度丢失的结果，可使用16进制的方式打印出更精确的double：

printf("%a\n",d1);

得到的输出结果为：

0x1.000000p+64

至此问题1实际上只是C++中，将高精度整数转double时的偶数舍入问题。

对于问题2，从float或double转换成int,值将会被向零舍入.例如1.999将被转换成1而-1.999将会被转换成-1。进一步来说，值有可能会溢出。C语言标准没有对这种情况指出固定的结果，这种转换行为是无定义的。

参考链接：

[1] http://en.wikipedia.org/wiki/Double-precision_floating-point_format#cite_note-whyieee-1

[2]深入理解计算机系统，Randal E. Bryant, 机械工业出版社

[3]http://stackoverflow.com/questions/4738768/printing-double-without-losing-precision

到此这篇关于C++中double浮点数精度丢失的深入分析的文章就介绍到这了,更多相关C++ double浮点数精度丢失内容请搜索小牛知识库以前的文章或继续浏览下面的相关文章希望大家以后多多支持小牛知识库！