java - IEEE-754单精度浮点数精度丢失有什么规律吗?
在单精度浮点数下,当我们输入的数字过大时会导致精度丢失。
比如 输入 16777217 实际存储是 16777216;输入 16777219 实际存储 16777220。
我好奇于为什么当输入 16777217 时就是减掉1,而输入 16777219 时就是加一。
- 这个是对应的单精度浮点数的存储格式
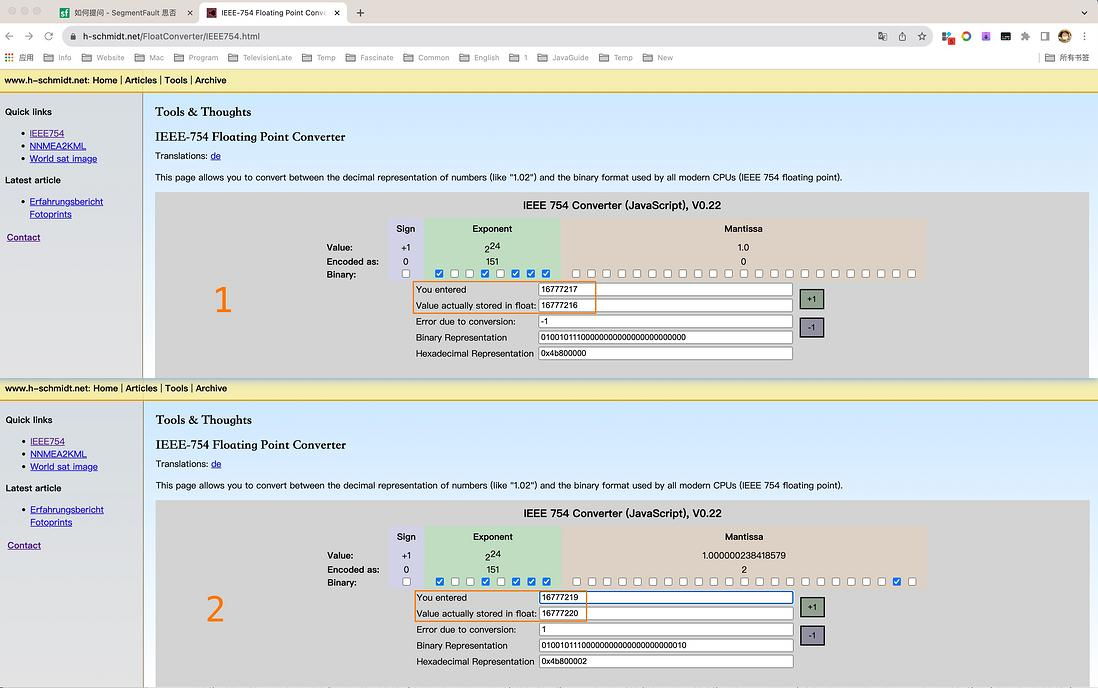
- 这个是我所列的转换误差的表格
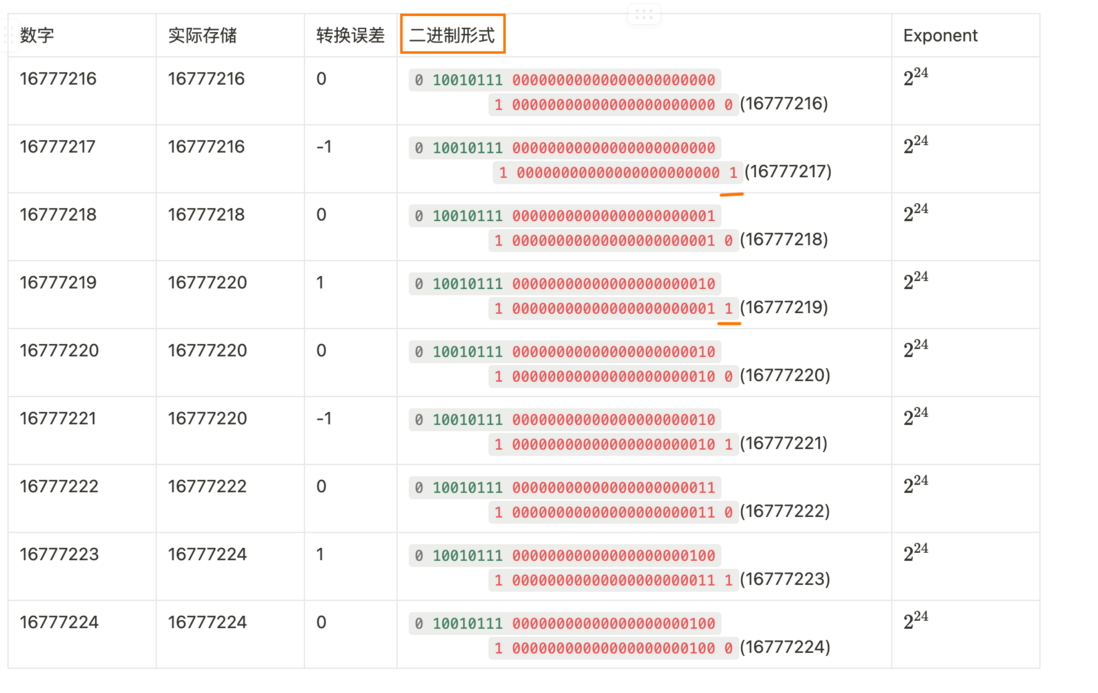
能够看出 输入 16777217 的时候实际存储时 尾数位的第24位是直接去掉的,相当于于减一
输入 的时候实际存储时 尾数为的第24位是在基础上加一,相当于逢二进一。
我的问题是 精度丢失是否可控?什么样趋势开始丢失精度,有没有什么规律?
换句话说就是为什么这个例子尾数位的第24位有的省略,有的则逢二进一呢?
共有2个答案
IEEE754 定义了若干种 rounding 方案,这里用的应该是 roundTiesToEven ,就是说当两个相邻的可表示值距离实际值相等的的时候,去最末尾为偶数(对二进制来说,就是0)的那一个。
这个和四舍五入类似,只是在 .1 (相当于十进制的 .5)的时候,有时进位,有时舍去。
=======
其它的 rounding 方案还有:
roundTiesToAway 这个类似四舍五入,只要 .1 就进一
roundTowardPositive 向大的方向取整(对正数来说,就是一律进一)
roundTowardNegative 向小的方向取整
roundTowardZero 向0取整
在 IEEE-754 单精度浮点数格式中,整数部分和小数部分都使用了 24 位来表示。对于给定的数字,其存储表示的精度丢失是由其二进制表示的特性决定的。
首先,对于输入的数 16777217,其二进制表示为:
10000000 00000000 00011111 11111111在转换为单精度浮点数时,整数部分(符号位和1位偏置)被保留,而小数部分被截断为 8 位,即只保留了原数的后 8 位,所以存储的实际值为:
10000000 00000000 00011111 11111110这个值与原数相比,尾数位的第24位是直接去掉的,相当于减一。
同样地,对于输入的数 16777219,其二进制表示为:
-
问题内容: 为什么单精度浮点数具有7位精度(或双精度15-16位精度)? 谁能解释一下如何根据为float(Sign(32)Exponent(30-23),Fraction(22-0))分配的32位来达到这个目标? 问题答案: 有效位的23个小数位(22-0)出现在内存格式中,但是总精度实际上是24位,因为我们假设有一个前导1。这等效于十进制数字。 双精度浮点数的分数为52位,加上前导1为53。因
-
问题内容: 与浮点变量一起使用时出现问题(向下舍入/截断精度部分)。如何正确执行? 游乐场:https : //play.golang.org/p/49TjJwwEdEJ 输出: 我期望的输出是的,但实际产量。 问题答案: 原始问题: Golang中的楼层号不正确 将Math.Floor与float变量一起使用时出现问题(向下舍入/截断精度部分)。我该怎么做呢? 我预计1980 * 0.1 / 1
-
问题内容: 我正在尝试将以下十六进制字符串转换为“ 41630D54FFF68872”到9988776.0(float-64)。 使用单精度float-32,我可以这样做: 但这会引发:java.lang.NumberFormatException:使用上面的64位十六进制时,Infinite或NaN。 如何将十六进制转换为使用64位IEEE-754编码的双精度浮点数? 谢谢 问题答案: 您需要双
-
问题内容: $a = ‘35’; $b = ‘-34.99’; echo ($a + $b); 结果为0.009999999999998 这是怎么回事?我想知道为什么我的程序不断报告奇怪的结果。 为什么PHP不返回预期的0.01? 问题答案: 因为浮点运算!=实数运算。对于一些浮子和,由不精确性引起的差异的说明是。这适用于使用浮点数的任何语言。 由于浮点数是具有有限精度的二进制数,因此存在有限数量
-
本文向大家介绍Fortran 浮点数精度,包括了Fortran 浮点数精度的使用技巧和注意事项,需要的朋友参考一下 示例 类型的浮点数real不能有任何实数值。它们可以表示实数,最多可以包含一定数量的十进制数字。 FORTRAN 77保证了两种浮点类型,而最新的标准则至少保证了两种实数类型。实变量可以声明为 x这是默认类型的实数,并且y是比更大的十进制精度的实数x。在Fortran 2008中,十
-
谢谢

