C语言实现图的最短路径Floyd算法

Floyd算法直接使用二维数组求出所有顶点到所有顶点的最短路径。

D代表顶点到顶点的最短路径权值和的矩阵。
P代表对应顶点的最小路径的前驱矩阵。

以下程序在DEV C++中调试运行通过。

#include <stdio.h> 
            
#define INFINITY 65535 
 
typedef int VertexType; //顶点是字符型 
typedef int EdgeType; //边是整型 
typedef struct //图的邻接矩阵存储结构 
{ 
 
 VertexType vexs[9]; //顶点向量 
 
 EdgeType edges[9][9];  //邻接矩阵 
 
 int vexnum,arcnum; //图中当前的顶点数和边数 
 
}MGraph; 
 
/* 邻接矩阵的建立*/ 
 
void CreateGraph(MGraph *G) 
{  
 int i,j,k,weight; 
 int ch1,ch2; 
 
 printf("请输入顶点数和边数(输入格式为:顶点数,边数):"); 
 
 scanf("%d,%d",&(G->vexnum),&(G->arcnum)); 
 
 printf("请输入顶点名称(输入格式为:a,b,c...)："); 
 
 for(i=0;i<G->vexnum;i++) 
 { 
  getchar(); 
  scanf("%d",&(G->vexs[i])); 
 } 
   
 for(i=0;i<G->vexnum;i++) 
  for(j=0;j<G->vexnum;j++) 
   if(i==j) 
    G->edges[i][j]=0; 
   else 
    G->edges[i][j]=INFINITY; 
 
  printf("请输入每条边对应的两个顶点名称(输入格式为:a,b):\n"); 
 
  for(k=0;k<G->arcnum;k++) 
  { 
   // getchar(); 
   printf("请输入第%d条边的两个顶点名称：",k+1); 
   scanf("%d,%d",&ch1,&ch2); 
   for(i=0;ch1!=G->vexs[i];i++); 
   for(j=0;ch2!=G->vexs[j];j++); 
   getchar(); 
   printf("请输入第%d条边的权值：",k+1); 
   scanf("%d",&weight);  
   G->edges[i][j]=weight; 
   G->edges[j][i]=weight; 
  } 
  
} 
 
void ShortestPath_Floyd(MGraph G,int P[9][9],int D[9][9]) 
{ 
 int v,w,k; 
 for(v=0;v<G.vexnum;v++)//初始化D和P 
 { 
  for(w=0;w<G.vexnum;w++) 
  { 
   D[v][w]=G.edges[v][w]; 
   P[v][w]=w; 
  } 
 } 
  
 for(k=0;k<G.vexnum;k++) 
 { 
  for(v=0;v<G.vexnum;v++) 
  { 
   for(w=0;w<G.vexnum;w++) 
   { 
    if(D[v][w]>(D[v][k]+D[k][w])) 
    {//如果经过下标为k顶点路径比原两点间路径更短，将当前两点间权值设为更小的一个 
    D[v][w]=D[v][k]+D[k][w]; 
    P[v][w]=P[v][k]; 
    } 
     
   } 
  } 
 } 
} 
void main() 
{ 
 MGraph G; 
 CreateGraph(&G); 
 int i,j; 
 printf("edgesnum:%d\n",G.arcnum); 
 printf("vexesnum:%d\n",G.vexnum); 
 for(i=0;i<9;i++) 
 { 
  for(j=0;j<9;j++) 
   printf("%d ",G.edges[i][j]); 
  printf("\n"); 
 } 
 int v,w,k; 
 int P[9][9]; 
 int D[9][9]; 
 printf("%d\n",P); 
 printf("%d\n",D); 
 ShortestPath_Floyd(G,P,D); 
 for(v=0;v<G.vexnum;v++)//显示路径 
 { 
  for(w=v+1;w<G.vexnum;w++) 
  { 
   printf("v%d-v%d weight:%d ",v,w,D[v][w]); 
   k=P[v][w]; 
   printf("path:%d",v); 
   while(k!=w) 
   { 
    printf("->%d",k); 
    k=P[k][w]; 
   } 
   printf("->%d\n",w); 
  } 
 } 
} 

运行结果如图所示。

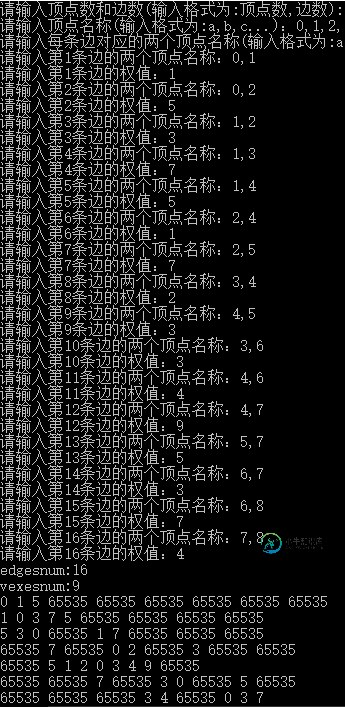
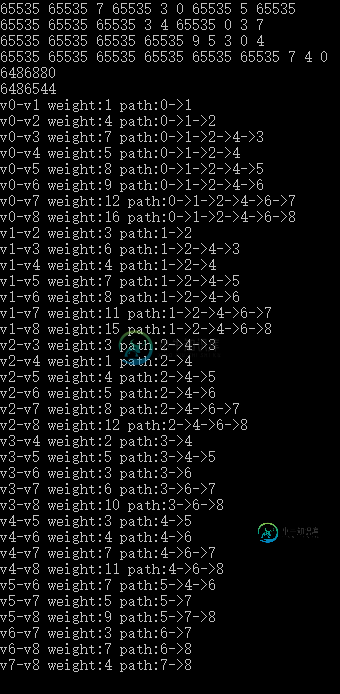
整个算法的时间复杂度是O(n^3)。

在编写过程中遇到了以下错误：
在62行
[Error]subscripted value is neither array nor pointer nor vector

意思是
下标的值不是数组或指针或向量
当时我这一行是这样写的
void ShortestPath_Floyd(MGraph G,int** P,int** D)
因为在上一篇文章Dijkstra算法中一维数组作为函数参数是用的int*，没有问题
所以在这里二维数组我就想当然地用了int**
但是如果参数传入int**类型，在函数里就不能使用P[v][w]访问二维数组的值

编译器不能正确为它寻址，需要模仿编译器的行为把P[v][w]这样的式子手工转变为：

     *((int*)P + n*v + w);

所以在被调用函数中对形参数组定义时可以指定所有维数的大小，也可以省略第一维的大小说明
故改为void ShortestPath_Floyd(MGraph G,int P[9][9],int D[9][9])就可以编译通过。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。