java实现Dijkstra最短路径算法

任务描述：在一个无向图中，获取起始节点到所有其他节点的最短路径描述

Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

Dijkstra一般的表述通常有两种方式，一种用永久和临时标号方式，一种是用OPEN, CLOSE表方式
用OPEN,CLOSE表的方式，其采用的是贪心法的算法策略，大概过程如下：

1.声明两个集合，open和close，open用于存储未遍历的节点，close用来存储已遍历的节点
2.初始阶段，将初始节点放入close，其他所有节点放入open
3.以初始节点为中心向外一层层遍历，获取离指定节点最近的子节点放入close并从新计算路径，直至close包含所有子节点

代码实例如下：

Node对象用于封装节点信息，包括名字和子节点

public class Node {
 private String name;
 private Map<Node,Integer> child=new HashMap<Node,Integer>();
 public Node(String name){
 this.name=name;
 }
 public String getName() {
 return name;
 }
 public void setName(String name) {
 this.name = name;
 }
 public Map<Node, Integer> getChild() {
 return child;
 }
 public void setChild(Map<Node, Integer> child) {
 this.child = child;
 }
}

MapBuilder用于初始化数据源，返回图的起始节点

public class MapBuilder {
 public Node build(Set<Node> open, Set<Node> close){
 Node nodeA=new Node("A");
 Node nodeB=new Node("B");
 Node nodeC=new Node("C");
 Node nodeD=new Node("D");
 Node nodeE=new Node("E");
 Node nodeF=new Node("F");
 Node nodeG=new Node("G");
 Node nodeH=new Node("H");
 nodeA.getChild().put(nodeB, 1);
 nodeA.getChild().put(nodeC, 1);
 nodeA.getChild().put(nodeD, 4);
 nodeA.getChild().put(nodeG, 5);
 nodeA.getChild().put(nodeF, 2);
 nodeB.getChild().put(nodeA, 1);
 nodeB.getChild().put(nodeF, 2);
 nodeB.getChild().put(nodeH, 4);
 nodeC.getChild().put(nodeA, 1);
 nodeC.getChild().put(nodeG, 3);
 nodeD.getChild().put(nodeA, 4);
 nodeD.getChild().put(nodeE, 1);
 nodeE.getChild().put(nodeD, 1);
 nodeE.getChild().put(nodeF, 1);
 nodeF.getChild().put(nodeE, 1);
 nodeF.getChild().put(nodeB, 2);
 nodeF.getChild().put(nodeA, 2);
 nodeG.getChild().put(nodeC, 3);
 nodeG.getChild().put(nodeA, 5);
 nodeG.getChild().put(nodeH, 1);
 nodeH.getChild().put(nodeB, 4);
 nodeH.getChild().put(nodeG, 1);
 open.add(nodeB);
 open.add(nodeC);
 open.add(nodeD);
 open.add(nodeE);
 open.add(nodeF);
 open.add(nodeG);
 open.add(nodeH);
 close.add(nodeA);
 return nodeA;
 }
}

图的结构如下图所示：

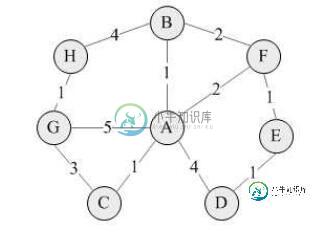
Dijkstra对象用于计算起始节点到所有其他节点的最短路径

public class Dijkstra {
 Set<Node> open=new HashSet<Node>();
 Set<Node> close=new HashSet<Node>();
 Map<String,Integer> path=new HashMap<String,Integer>();//封装路径距离
 Map<String,String> pathInfo=new HashMap<String,String>();//封装路径信息
 public Node init(){
 //初始路径,因没有A->E这条路径,所以path(E)设置为Integer.MAX_VALUE
 path.put("B", 1);
 pathInfo.put("B", "A->B");
 path.put("C", 1);
 pathInfo.put("C", "A->C");
 path.put("D", 4);
 pathInfo.put("D", "A->D");
 path.put("E", Integer.MAX_VALUE);
 pathInfo.put("E", "A");
 path.put("F", 2);
 pathInfo.put("F", "A->F");
 path.put("G", 5);
 pathInfo.put("G", "A->G");
 path.put("H", Integer.MAX_VALUE);
 pathInfo.put("H", "A");
 //将初始节点放入close,其他节点放入open
 Node start=new MapBuilder().build(open,close);
 return start;
 }
 public void computePath(Node start){
 Node nearest=getShortestPath(start);//取距离start节点最近的子节点,放入close
 if(nearest==null){
 return;
 }
 close.add(nearest);
 open.remove(nearest);
 Map<Node,Integer> childs=nearest.getChild();
 for(Node child:childs.keySet()){
 if(open.contains(child)){//如果子节点在open中
 Integer newCompute=path.get(nearest.getName())+childs.get(child);
 if(path.get(child.getName())>newCompute){//之前设置的距离大于新计算出来的距离
  path.put(child.getName(), newCompute);
  pathInfo.put(child.getName(), pathInfo.get(nearest.getName())+"->"+child.getName());
 }
 }
 }
 computePath(start);//重复执行自己,确保所有子节点被遍历
 computePath(nearest);//向外一层层递归,直至所有顶点被遍历
 }
 public void printPathInfo(){
 Set<Map.Entry<String, String>> pathInfos=pathInfo.entrySet();
 for(Map.Entry<String, String> pathInfo:pathInfos){
 System.out.println(pathInfo.getKey()+":"+pathInfo.getValue());
 }
 }
 /**
 * 获取与node最近的子节点
 */
 private Node getShortestPath(Node node){
 Node res=null;
 int minDis=Integer.MAX_VALUE;
 Map<Node,Integer> childs=node.getChild();
 for(Node child:childs.keySet()){
 if(open.contains(child)){
 int distance=childs.get(child);
 if(distance<minDis){
  minDis=distance;
  res=child;
 }
 }
 }
 return res;
 }
}

Main用于测试Dijkstra对象

public class Main {
 public static void main(String[] args) {
 Dijkstra test=new Dijkstra();
 Node start=test.init();
 test.computePath(start);
 test.printPathInfo();
 }
}

打印输出如下：

D:A->D
E:A->F->E
F:A->F
G:A->C->G
B:A->B
C:A->C
H:A->B->H

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。