python编写的最短路径算法
一心想学习算法,很少去真正静下心来去研究,前几天趁着周末去了解了最短路径的资料,用python写了一个最短路径算法。算法是基于带权无向图去寻找两个点之间的最短路径,数据存储用邻接矩阵记录。首先画出一幅无向图如下,标出各个节点之间的权值。
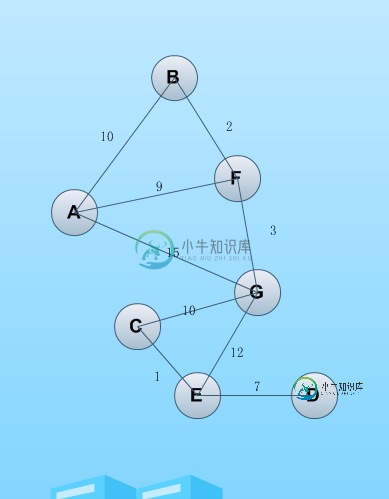
其中对应索引:
A ——> 0
B——> 1
C——> 2
D——>3
E——> 4
F——> 5
G——> 6
邻接矩阵表示无向图:

算法思想是通过Dijkstra算法结合自身想法实现的。大致思路是:从起始点开始,搜索周围的路径,记录每个点到起始点的权值存到已标记权值节点字典A,将起始点存入已遍历列表B,然后再遍历已标记权值节点字典A,搜索节点周围的路径,如果周围节点存在于表B,比较累加权值,新权值小于已有权值则更新权值和来源节点,否则什么都不做;如果不存在与表B,则添加节点和权值和来源节点到表A,直到搜索到终点则结束。
这时最短路径存在于表A中,得到终点的权值和来源路径,向上递推到起始点,即可得到最短路径,下面是代码:
# -*-coding:utf-8 -*-
class DijkstraExtendPath():
def __init__(self, node_map):
self.node_map = node_map
self.node_length = len(node_map)
self.used_node_list = []
self.collected_node_dict = {}
def __call__(self, from_node, to_node):
self.from_node = from_node
self.to_node = to_node
self._init_dijkstra()
return self._format_path()
def _init_dijkstra(self):
self.used_node_list.append(self.from_node)
self.collected_node_dict[self.from_node] = [0, -1]
for index1, node1 in enumerate(self.node_map[self.from_node]):
if node1:
self.collected_node_dict[index1] = [node1, self.from_node]
self._foreach_dijkstra()
def _foreach_dijkstra(self):
if len(self.used_node_list) == self.node_length - 1:
return
for key, val in self.collected_node_dict.items(): # 遍历已有权值节点
if key not in self.used_node_list and key != to_node:
self.used_node_list.append(key)
else:
continue
for index1, node1 in enumerate(self.node_map[key]): # 对节点进行遍历
# 如果节点在权值节点中并且权值大于新权值
if node1 and index1 in self.collected_node_dict and self.collected_node_dict[index1][0] > node1 + val[0]:
self.collected_node_dict[index1][0] = node1 + val[0] # 更新权值
self.collected_node_dict[index1][1] = key
elif node1 and index1 not in self.collected_node_dict:
self.collected_node_dict[index1] = [node1 + val[0], key]
self._foreach_dijkstra()
def _format_path(self):
node_list = []
temp_node = self.to_node
node_list.append((temp_node, self.collected_node_dict[temp_node][0]))
while self.collected_node_dict[temp_node][1] != -1:
temp_node = self.collected_node_dict[temp_node][1]
node_list.append((temp_node, self.collected_node_dict[temp_node][0]))
node_list.reverse()
return node_list
def set_node_map(node_map, node, node_list):
for x, y, val in node_list:
node_map[node.index(x)][node.index(y)] = node_map[node.index(y)][node.index(x)] = val
if __name__ == "__main__":
node = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
node_list = [('A', 'F', 9), ('A', 'B', 10), ('A', 'G', 15), ('B', 'F', 2),
('G', 'F', 3), ('G', 'E', 12), ('G', 'C', 10), ('C', 'E', 1),
('E', 'D', 7)]
node_map = [[0 for val in xrange(len(node))] for val in xrange(len(node))]
set_node_map(node_map, node, node_list)
# A -->; D
from_node = node.index('A')
to_node = node.index('D')
dijkstrapath = DijkstraPath(node_map)
path = dijkstrapath(from_node, to_node)
print path
运行结果:
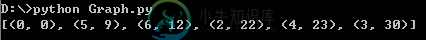
再来一例:
<!-- lang: python -->
# -*- coding: utf-8 -*-
import itertools
import re
import math
def combination(lst): #全排序
lists=[]
liter=itertools.permutations(lst)
for lts in list(liter):
lt=''.join(lts)
lists.append(lt)
return lists
def coord(lst): #坐标输入
coordinates=dict()
print u'请输入坐标:(格式为A:7 17)'
p=re.compile(r"\d+")
for char in lst:
str=raw_input(char+':')
dot=p.findall(str)
coordinates[char]=[dot[0],dot[1]]
print coordinates
return coordinates
def repeat(lst): #删除重复组合
for ilist in lst:
for k in xrange(len(ilist)):
st=(ilist[k:],ilist[:k])
strs=''.join(st)
for jlist in lst:
if(cmp(strs,jlist)==0):
lst.remove(jlist)
for k in xrange(len(ilist)):
st=(ilist[k:],ilist[:k])
strs=''.join(st)
for jlist in lst:
if(cmp(strs[::-1],jlist)==0):
lst.remove(jlist)
lst.append(ilist)
print lst
return lst
def count(lst,coordinates): #计算各路径
way=dict()
for str in lst:
str=str+str[:1]
length=0
for i in range(len(str)-1):
x=abs( float(coordinates[str[i]][0]) - float(coordinates[str[i+1]][0]) )
y=abs( float(coordinates[ str[i] ][1]) - float(coordinates[ str[i+1] ][1]) )
length+=math.sqrt(x**2+y**2)
way[str[:len(str)-1]]=length
return way
if __name__ =="__main__":
print u'请输入图节点:'
rlist=list(raw_input())
coordinates=coord(rlist)
list_directive = combination(rlist)
# print "有方向完全图所有路径为:",list_directive
# for it in list_directive:
# print it
print u'有方向完全图所有路径总数:',len(list_directive),"\n"
#无方向完全图
list_directive=repeat(list_directive)
list_directive=repeat(list_directive)
# print "无方向完全图所有路径为:",list_directive
print u'无方向完全图所有路径为:'
for it in list_directive:
print it
print u'无方向完全图所有路径总数:',len(list_directive)
ways=count(list_directive,coordinates)
print u'路径排序如下:'
for dstr in sorted(ways.iteritems(), key=lambda d:d[1], reverse = False ):
print dstr
raw_input()
以上就是本文给大家分享的全部内容了,希望大家能够喜欢,能够学习python有所帮助。
请您花一点时间将文章分享给您的朋友或者留下评论。我们将会由衷感谢您的支持!
-
主要内容:最短路径算法在给定的图存储结构中,从某一顶点到另一个顶点所经过的多条边称为 路径。 图 1 图存储结构 例如在图 1 所示的图结构中,从顶点 A 到 B 的路径有多条,包括 A-B、A-C-B 和 A-D-B。当我们给图中的每条边赋予相应的权值后,就可以从众多路径中找出总权值最小的一条,这条路径就称为 最短路径。 图 2 无向带权图 以图 2 为例,从顶点 A 到 B 的路径有 3 条,它们各自的总权值是:
-
本文向大家介绍Javascript中的最短路径算法,包括了Javascript中的最短路径算法的使用技巧和注意事项,需要的朋友参考一下 在图论中,最短路径问题是在图中的两个顶点(或节点)之间找到路径的问题,以使其构成边的权重之和最小。在这里,我们需要修改添加边缘并添加有向方法,以允许向边缘添加权重。 让我们看看如何添加它- 示例 现在,当在图上添加一条边时,如果我们不指定权重,则会为该边分配默认
-
本文向大家介绍python实现Dijkstra算法的最短路径问题,包括了python实现Dijkstra算法的最短路径问题的使用技巧和注意事项,需要的朋友参考一下 迪杰斯特拉(Dijkstra)算法主要是针对没有负值的有向图,求解其中的单一起点到其他顶点的最短路径算法。 1 算法原理 迪杰斯特拉(Dijkstra)算法是一个按照路径长度递增的次序产生的最短路径算法。下图为带权值的有向图,作为程序中
-
最短路径问题的Dijkstra算法 是由荷兰计算机科学家艾兹赫尔·戴克斯特拉提出。迪科斯彻算法使用了广度优先搜索解决非负权有向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。 这个算法的python实现途径很多,网上能够发现不少。这里推荐一个我在网上看到的,本来打算自己写,看了这个,决定自己不写了,因为他的已经太好了。 解决(Python) #
-
你好,亲爱的朋友们。 我想在随机图中找到最短路径。我使用boost图形库。据我所知,我需要利用点之间的现有距离构建图形。之后,我需要使用一些算法。。。 正如我所见,Dijkstra的算法实际上是找到从1点到其他点的所有路径。(应该很慢?) A*需要一些额外的数据(不仅仅是距离) 如何找到2点之间的最短路径?我在bgl文件夹中看到了许多最短路径算法标头,但我没有找到如何使用它们的示例。 此外,我可以
-
我已经从Cormen的第三版参考“算法介绍”中找到的伪代码中实现了Dijkstra算法,用于单源最短路径问题。 我的实现是在python上使用链接列表在邻接列表表示中表示图形。这意味着节点列表是一个链接列表,每个节点都有一个链接列表来表示每个节点的边缘。此外,我没有实现或使用任何二进制堆或斐波那契堆作为算法所需的最小优先级队列,因此当过程需要提取与源距离最小的下一个节点时,我在节点链表内搜索O(V

