如何计算具有加权顶点的图的最短路径?
我试图弄清楚,如何计算具有加权顶点的图的最短路径。经典算法,如Dijkstra和Floyd-WarMarshall,通常使用加权边,我看不到如何将它们应用于我的情况(加权顶点):
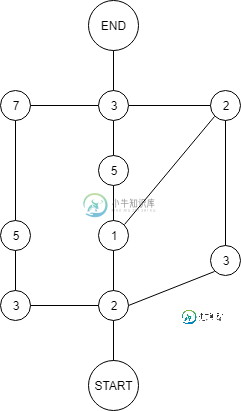
我的一个想法是将图形转换为带有加权边的更经典的视图。这是我收到的:
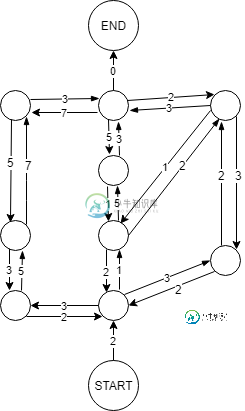
这里我们有单向和双向加权边,但我仍然不确定哪种算法可以处理这一点,以找到最短路径。
共有2个答案
您可以将问题简化为经典的最短路径问题,并根据需要使用Dijkstra、Bellman Ford或Floyd Warshal。为了简单起见,在下面的内容中,我假设所有权重都是非负的。我认为这样的假设是合理的,因为问题提到使用Dijkstra算法来解决问题。最后,可以谨慎地消除这种假设。
考虑问题的最一般形式:假设G=
总之,对于原始图形中的任何顶点,在H中添加两个顶点,一个专用于输入边,另一个专用于输出边(此外,根据G中相应顶点的权重,连接H中的新相关节点)。
现在,有一个有向加权图H,它在顶点上没有权重,但只在边上。很容易证明(s_in,t_out)inH之间的最短路径与原始图G中(s,t)之间的最短路径相同。
该证明基于这样一个事实,即任何这样的路径都通过(v_in,v_out)inH当且仅当G中的相应路径通过节点v。
就分析而言,我们有|V'|=2 |V |,和|E'|=E | | V |。因此,这种归约不会影响所采用的最短路径算法的渐近行为。
你当然可以通过转换图来做到这一点。最简单的方法是将每条边转换成一个顶点,并将新的顶点与成本与过去连接它们的顶点相同的边连接在一起。
但你真的不需要为这些烦恼。。。
Dijkstra的算法很容易适应顶点代价,而不需要使用任何这样的变换。当你遍历一条边时,你只需要做新的顶点成本=旧的顶点成本-边权重,而不是新的顶点成本=旧的顶点成本-新的顶点权重。
-
以下是消费税: 在某些图的问题中,顶点可以有权代替边的权或增加边的权。设Cv是顶点v的代价,C(x,y)是边(x,y)的代价。该问题涉及到在图G中寻找顶点a和顶点b之间的最便宜路径,路径的代价是该路径上遇到的边和顶点的代价之和。 (a)假设图中每条边的权重为零(而非边的代价为∞),假设所有顶点1≤V≤n(即所有顶点的代价相同),Cv=1。给出一个求从a到b最便宜路径的高效算法及其时间复杂度。 (b
-
因此,如果我在一个图中有两个顶点,它们通过一个以上的边连接,而它们之间有相同的最短路径(即,如果我有节点a和节点B,它们直接通过三条边连接(它们之间有三条最短路径,每个距离为1),所以计数应该返回3)我该如何修改BFS算法来实现这一点?这是我的代码,它只计算2个节点之间的最短路径,而不计算这些最短路径的个数。
-
给定一些无向边加权图,什么算法可以用来找到从某个顶点v到另一个顶点w的最短路径? 对于有向边加权图,可以使用Dijkstra的最短路径算法,但我使用的是无向图,所以它不起作用。 对于非边加权的图,可以使用广度优先搜索(BFS),但我使用的是边加权图,所以它不起作用。 既然它是无向和边加权的,一般最短路径法是什么?
-
在无向赋权图中寻找两个顶点之间的最短路径。还已知权重是小于log(logV)的整数,其中V是顶点的数量。使用贝尔曼-福特或Dijkstra算法很容易解决,但是有没有什么算法可以更快地解决呢? 到目前为止,我一直在考虑使用BFS,将权重大于1的边划分成两个权重为1的边,但如果V是大数,就不是一个好主意。不,这不是我的家庭作业,我只是在想。
-
在一个加权有向图中,我需要找到两个结点s,t之间的最短路径。以下是限制: 权重可以为负值。 路径必须经过一个特定的边,让我们从节点u到V调用her e和shes。 输出路径必须简单,即我们只通过一个节点一次。 因为我希望它最短,所以我将检查在从s到u之前从v到t运行bellman ford是否比相反的方式更快(如果有节点,两个节点都使用where是放置它的最佳位置)。 谢谢你的帮助!
-
然而,出现的问题是,当我将一个顶点设置为一个旅游站点并给它一个权重时,该顶点在第一次访问时似乎根本没有权重。然后,当第二次访问顶点时,权重显示出来。我不知道问题出在哪里,但我猜是因为我没有直接编辑原始变量。 打印输出行标记在下面的**之间。一个在calculateShortest()中,另一个在calculateMin()中。 显示问题的行打印输出(不包括main方法输出):

